Skip to main content
SpringerLink
Log in

A novel wavelets operational matrix method for the time variable-order fractional mobile–immobile advection–dispersion model

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

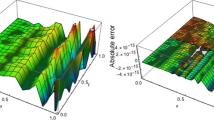
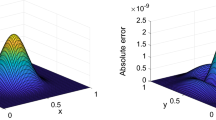
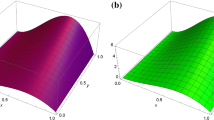
A novel computational technique for the solution of the variable-order fractional mobile–immobile advection–dispersion equation has been presented in this paper. Firstly, operational integration matrices and variable-order fractional derivatives were deduced using Boubaker wavelets to implement this proposed technique. Utilizing Boubaker wavelets basis for functions approximations and the operational matrices of integration and variable-order fractional derivative along with collocation points, the variable-order fractional mobile–immobile advection–dispersion equation is reduced into the system of algebraic equations. In addition, to determine the convergence analysis and error estimate of the proposed numerical technique, some useful theorems are discussed. Finally, to analyze the computational efficiency and applicability of the proposed numerical method, several numerical examples are presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Samko SG, Ross B (1993) Integration and differentiation to a variable fractional order. Integr Transf Spec Funct 1(4):277–300

    Article  MathSciNet  MATH  Google Scholar 

  2. Roohi R, Heydari MH, Sun HG (2019) Numerical study of unsteady natural convection of variable-order fractional Jeffrey nanofluid over an oscillating plate in a porous medium involved with magnetic, chemical and heat absorption effects using Chebyshev cardinal functions. Eur Phys J Plus 134:535

    Article  Google Scholar 

  3. Saha Ray S, Sahoo S (2018) Generalized fractional order differential equations arising in physical models. CRC Press, Boca Raton

    MATH  Google Scholar 

  4. Saha Ray S, Sahoo S, Das S (2016) Formulation and solutions of fractional continuously variable order mass–spring–damper systems controlled by viscoelastic and viscous–viscoelastic dampers. Adv Mech Eng 8(5):1–13

    Google Scholar 

  5. Sahoo S, Saha Ray S, Das S (2017) An efficient and novel technique for solving continuously variable fractional order mass-spring-damping system. Eng Comput 34(8):2815–2835

    Article  Google Scholar 

  6. Hosseininia M, Heydari MH, Avazzadeh Z (2020) Numerical study of the variable-order fractional version of the nonlinear fourth-order 2D diffusion-wave equation via 2D Chebyshev wavelets. Eng Comput. https://doi.org/10.1007/s00366-020-00995-z

    Article  MATH  Google Scholar 

  7. Zhuang P, Liu F, Anh V, Turner I (2009) Numerical methods for the variable-order fractional advection-diffusion equation with a nonlinear source term. SIAM J Numer Anal 47(3):1760–1781. https://doi.org/10.1137/080730597

    Article  MathSciNet  MATH  Google Scholar 

  8. Zhao X, Sun Z, Karniadakis GE (2015) Second-order approximations for variable order fractional derivatives: algorithms and applications. J Comput Phys 293:184–200

    Article  MathSciNet  MATH  Google Scholar 

  9. Zhang H, Liu F, Phanikumar MS, Meerschaert MM (2013) A novel numerical method for the time variable fractional order mobile–immobile advection–dispersion model. Comput Math Appl 66(5):693–701

    Article  MathSciNet  MATH  Google Scholar 

  10. Saha Ray S (2021) A new approach by two-dimensional wavelets operational matrix method for solving variable-order fractional partial integro-differential equations. Numer Methods Partial Differ Equ 37(1):341–359

    Article  MathSciNet  Google Scholar 

  11. Bear J (1972) Dynamics of fluids in porous media. American Elsevier Publishing Company, New York

    MATH  Google Scholar 

  12. Golbabai A, Nikan O, Nikazad T (2019) Numerical investigation of the time fractional mobile-immobile advection-dispersion model arising from solute transport in porous media. Int J Appl Comput Math 5:50

    Article  MathSciNet  MATH  Google Scholar 

  13. Sun L, Qiu H, Wu C, Niu J, Hu BX (2020) A review of applications of fractional advection–dispersion equations for anomalous solute transport in surface and subsurface water. WIREs Water 7(4):e1448

    Article  Google Scholar 

  14. Sun H, Chen W, Chen Y (2009) Variable-order fractional differential operators in anomalous diffusion modeling. Phys A 388:4586–4592

    Article  Google Scholar 

  15. Abdelkawy MA, Zaky MA, Bhrawy AH, Baleanu D (2015) Numerical simulation of time variable fractional order mobile-immobile advection-dispersion model. Romanian Rep Phys 67(3):773–791

    Google Scholar 

  16. Liu Z, Li X (2018) A Crank-Nicolson difference scheme for the time variable fractional mobile–immobile advection–dispersion equation. J Appl Math Comput 56:391–410

    Article  MathSciNet  MATH  Google Scholar 

  17. Schumer R, Benson DA, Meerschaert MM, Baeumer B (2003) Fractal mobile/immobile solute transport. Water Resour Res 39(10):1296

    Article  Google Scholar 

  18. Liu Q, Liu F, Turner I, Anh V, Gu YT (2014) A RBF meshless approach for modeling a fractal mobile/immobile transport model. Appl Math Comput 226:336–347

    MathSciNet  MATH  Google Scholar 

  19. Liu F, Zhuang P, Burrage K (2012) Numerical methods and analysis for a class of fractional advection–dispersion models. Comput Math Appl 64(10):2990–3007

    Article  MathSciNet  MATH  Google Scholar 

  20. Shen S, Liu F, Chen J, Turner I, Anh V (2012) Numerical techniques for the variable order time fractional diffusion equation. Appl Math Comput 218(22):10861–10870

    MathSciNet  MATH  Google Scholar 

  21. Sahoo S, Saha Ray S, Das S, Bera RK (2016) The formation of dynamic variable order fractional differential equation. Int J Mod Phys C 27(7):12. https://doi.org/10.1142/S0129183116500741 (Article number 1650074)

    Article  MathSciNet  Google Scholar 

  22. Bolandtalat A, Babolian E, Jafari H (2016) Numerical solutions of multi-order fractional differential equations by Boubaker polynomials. Open Phys 14:226–230. https://doi.org/10.1515/phys-2016-0028

    Article  Google Scholar 

  23. Rabiei K, Ordokhani Y (2020) A new operational matrix based on Boubaker wavelet for solving optimal control problems of arbitrary order. Trans Inst Meas Control 42(10):1858–1870

    Article  Google Scholar 

  24. Saha Ray S, Behera S (2019) Two-dimensional wavelets operational method for solving Volterra weakly singular partial integro-differential equations. J Comput Appl Math. https://doi.org/10.1016/j.cam.2019.112411

    Article  MATH  Google Scholar 

  25. Behera S, Saha Ray S (2019) An operational matrix based scheme for numerical solutions of nonlinear weakly singular partial integro-differential equations. Appl Math Comput. https://doi.org/10.1016/j.amc.2019.124771

    Article  MATH  Google Scholar 

  26. Canuto C, Hussaini MY, Quarteroni A, Zang TA (2006) Spectral methods. Fundamentals in single domains scientific computation. Springer, Berlin

    Book  MATH  Google Scholar 

  27. Marzban HR, Tabrizidooz HR, Razzaghi M (2011) A composite collocation method for the nonlinear mixed Volterra–Fredholm–Hammerstein integral equations. Commun Nonlinear Sci Numer Simul 16(3):1186–1194

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, National Institute of Technology, Rourkela, 769008, India

    S. Saha Ray

Authors
  1. S. Saha Ray
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Saha Ray.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ray, S.S. A novel wavelets operational matrix method for the time variable-order fractional mobile–immobile advection–dispersion model. Engineering with Computers 38 (Suppl 4), 2629–2650 (2022). https://doi.org/10.1007/s00366-021-01405-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-021-01405-8

Keywords

Search

Navigation