Abstract
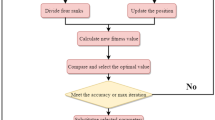
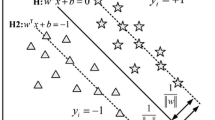
The prediction of the potential of soil liquefaction induced by the earthquake is a vital task in construction engineering and geotechnical engineering. To provide a possible solution to such problems, this paper proposes two support vector machine (SVM) models which are optimized by genetic algorithm (GA) and grey wolf optimizer (GWO) to predict the potential of soil liquefaction. Field observation data based on cone penetration test (CPT), standard penetration test (SPT) and shear wave velocity (VS) test (SWVT) are employed to verify the reliability of the GA–SVM model and the GWO–SVM model, the numbers of input variables of these three field testing data sets are 6, 12 and 8, respectively, and the output result is the potential of soil liquefaction. To verify whether the two optimization algorithms GA and GWO have significantly improved the performance of SVM model, an unoptimized SVM model is served as a reference in this study. And five performance metrics, including classification accuracy rate (ACC), precision rate (PRE), recall rate (REC), F1 score (F1) and AUC are used to evaluate the classification performance of the three models. Results of the study confirm that when CPT-based, SPT-based and SWVT-based test sets are input into three classification models, the highest classification accuracy of 0.9825, 0.9032 and 0.9231, respectively, is achieved with GWO–SVM. And based on these three data sets, the values of AUC obtained by GWO–SVM are all higher than those obtained by GA–SVM. Further, by comparing the other metrics of the three classification models, it is found that the classification performance of the two hybrid models is very similar and significantly better than the SVM, which indicates that GWO–SVM, like GA–SVM, can also be used as a reliable model for predicting soil liquefaction potential.

















Similar content being viewed by others
References
Samui P, Sitharam TG (2011) Machine learning modelling for predicting soil liquefaction susceptibility. Nat Hazard 11:1–9. https://doi.org/10.5194/nhess-11-1-2011
Bhattacharya S, Hyodo M, Goda K et al (2011) Liquefaction of soil in the Tokyo Bay area from the 2011 Tohoku (Japan) earthquake. Soil Dyn Earthq Eng 31:1618–1628. https://doi.org/10.1016/j.soildyn.2011.06.006
Samui P, Karthikeyan J (2013) Determination of liquefaction susceptibility of soil: a least square support vector machine approach. Int J Numer Anal Meth Geomech 37:1154–1161. https://doi.org/10.1002/nag.2081
Zhao H-B, Ru Z-L, Yin S (2007) Updated support vector machine for seismic liquefaction evaluation based on the penetration tests. Mar Georesour Geotechnol 25:209–220. https://doi.org/10.1080/10641190701702303
Juang CH, Chen CJ (2000) A rational method for development of limit state for liquefaction evaluation based on shear wave velocity measurements. Int J Numer Anal Meth Geomech 24:1–27
Juang CH, Chen CJ, Tang WH et al (2000) CPT-based liquefaction analysis, Part 1: Determination of limit state function. Geotechnique 50:583–592. https://doi.org/10.1680/geot.2000.50.5.583
Juang CH, Yuan HM, Lee DH et al (2003) Simplified cone penetration test-based method for evaluating liquefaction resistance of soils. J Geotech Geoenviron Eng 129:66–80. https://doi.org/10.1061/(asce)1090-0241(2003)129:1(66)
Seo M-W, Olson SM, Sun C-G et al (2012) Evaluation of liquefaction potential index along western coast of South Korea Using SPT and CPT. Mar Georesour Geotechnol 30:234–260. https://doi.org/10.1080/1064119x.2011.614322
Hoang ND, Bui DT (2018) Predicting earthquake-induced soil liquefaction based on a hybridization of kernel Fisher discriminant analysis and a least squares support vector machine: a multi-dataset study. Bull Eng Geol Env 77:191–204. https://doi.org/10.1007/s10064-016-0924-0
Pal M (2006) Support vector machines-based modelling of seismic liquefaction potential. Int J Numer Anal Meth Geomech 30:983–996. https://doi.org/10.1002/nag.509
Zhang JF, Wang YH (2021) An ensemble method to improve prediction of earthquake-induced soil liquefaction: a multi-dataset study. Neural Comput Appl 33:1533–1546. https://doi.org/10.1007/s00521-020-05084-2
Hanna AM, Ural D, Saygili G (2007) Evaluation of liquefaction potential of soil deposits using artificial neural networks. Eng Comput 24:5–16. https://doi.org/10.1108/02644400710718547
Zhou J, Li XB, Shi XZ (2012) Long-term prediction model of rockburst in underground openings using heuristic algorithms and support vector machines. Saf Sci 50:629–644. https://doi.org/10.1016/j.ssci.2011.08.065
Shi XZ, Zhou J, Wu BB et al (2012) Support vector machines approach to mean particle size of rock fragmentation due to bench blasting prediction. Trans Nonferrous Met Soc China 22:432–441. https://doi.org/10.1016/s1003-6326(11)61195-3
Zhou J, Li XB, Mitri HS (2015) Comparative performance of six supervised learning methods for the development of models of hard rock pillar stability prediction. Nat Hazards 79:291–316. https://doi.org/10.1007/s11069-015-1842-3
Hoang ND, Pham AD (2016) Hybrid artificial intelligence approach based on metaheuristic and machine learning for slope stability assessment: a multinational data analysis. Expert Syst Appl 46:60–68. https://doi.org/10.1016/j.eswa.2015.10.020
Sharma LK, Vishal V, Singh TN (2017) Developing novel models using neural networks and fuzzy systems for the prediction of strength of rocks from key geomechanical properties. Measurement 102:158–169. https://doi.org/10.1016/j.measurement.2017.01.043
Khandelwal M, Marto A, Fatemi SA et al (2018) Implementing an ANN model optimized by genetic algorithm for estimating cohesion of limestone samples. Eng Comput 34:307–317. https://doi.org/10.1007/s00366-017-0541-y
Zhou J, Li EM, Yang S et al (2019) Slope stability prediction for circular mode failure using gradient boosting machine approach based on an updated database of case histories. Saf Sci 118:505–518. https://doi.org/10.1016/j.ssci.2019.05.046
Zhou J, Koopialipoor M, Li EM et al (2020) Prediction of rockburst risk in underground projects developing a neuro-bee intelligent system. Bull Eng Geol Env 79:4265–4279. https://doi.org/10.1007/s10064-020-01788-w
Zhou J, Asteris PG, Armaghani DJ et al (2020) Prediction of ground vibration induced by blasting operations through the use of the Bayesian Network and random forest models. Soil Dyn Earthq Eng 139:106390. https://doi.org/10.1016/j.soildyn.2020.106390
Zhou J, Qiu Y, Zhu S et al (2020) Estimation of the TBM advance rate under hard rock conditions using XGBoost and Bayesian optimization. Underground Space. https://doi.org/10.1016/j.undsp.2020.05.008
Guo H, Zhou J, Koopialipoor M et al (2021) Deep neural network and whale optimization algorithm to assess flyrock induced by blasting. Eng Comput 37:173–186. https://doi.org/10.1007/s00366-019-00816-y
Zhou J, Li C, Arslan CA et al (2021) Performance evaluation of hybrid FFA-ANFIS and GA-ANFIS models to predict particle size distribution of a muck-pile after blasting. Eng Comput 37:265–274. https://doi.org/10.1007/s00366-019-00822-0
Yu Z, Shi XZ, Zhou J et al (2021) Feasibility of the indirect determination of blast-induced rock movement based on three new hybrid intelligent models. Eng Comput 37:991–1006. https://doi.org/10.1007/s00366-019-00868-0
Wang S-m, Zhou J, Li C-q et al (2021) Rockburst prediction in hard rock mines developing bagging and boosting tree-based ensemble techniques. J Central South University 28:527–542. https://doi.org/10.1007/s11771-021-4619-8
Qiu Y, Zhou J, Khandelwal M et al (2021) Performance evaluation of hybrid WOA-XGBoost, GWO-XGBoost and BO-XGBoost models to predict blast-induced ground vibration. Eng Comput https://doi.org/https://doi.org/10.1007/s00366-021-01393-9
Wei W, Li X, Liu J et al (2021) Performance Evaluation of Hybrid WOA-SVR and HHO-SVR Models with Various Kernels to Predict Factor of Safety for Circular Failure Slope. Applied Sciences-Basel 11. doi:https://doi.org/10.3390/app11041922
Zhou J, Qiu Y, Armaghani DJ et al (2021) Predicting TBM penetration rate in hard rock condition: A comparative study among six XGB-based metaheuristic techniques. Geoscience Frontiers 12(3), 101091
Hanna AM, Ural D, Saygili G (2007) Neural network model for liquefaction potential in soil deposits using Turkey and Taiwan earthquake data. Soil Dyn Earthq Eng 27:521–540. https://doi.org/10.1016/j.soildyn.2006.11.001
Samui P, Kim D, Sitharam TG (2011) Support vector machine for evaluating seismic-liquefaction potential using shear wave velocity. J Appl Geophys 73:8–15. https://doi.org/10.1016/j.jappgeo.2010.10.005
Venkatesh K, Kumar V, Tiwari RP (2013) Appraisal of liquefaction potential using neural network and neuro fuzzy approach. Appl Artif Intell 27:700–720. https://doi.org/10.1080/08839514.2013.823326
Muduli PK, Das SK, Bhattacharya S (2014) CPT-based probabilistic evaluation of seismic soil liquefaction potential using multi-gene genetic programming. Georisk 8:14–28. https://doi.org/10.1080/17499518.2013.845720
Xue X, Yang X, Li P (2017) Application of a probabilistic neural network for liquefaction assessment. Neural Network World 27:557–567. https://doi.org/10.14311/NNW.2017.27.030
Xue X, Liu E (2017) Seismic liquefaction potential assessed by neural networks. Environ Earth Sci 76. doi:https://doi.org/10.1007/s12665-017-6523-y
Zhou J, Li EM, Wang MZ et al (2019) Feasibility of Stochastic Gradient Boosting Approach for Evaluating Seismic Liquefaction Potential Based on SPT and CPT Case Histories. J Perform Constr Facil 33. doi:https://doi.org/10.1061/(asce)cf.1943-5509.0001292
Alobaidi MH, Meguid MA, Chebana F (2019) Predicting seismic-induced liquefaction through ensemble learning frameworks. Sci Rep 9. doi:https://doi.org/10.1038/s41598-019-48044-0
Ramakrishnan D, Singh TN, Purwar N et al (2008) Artificial neural network and liquefaction susceptibility assessment: a case study using the 2001 Bhuj earthquake data, Gujarat, India. Comput Geosci 12:491–501. https://doi.org/10.1007/s10596-008-9088-8
Erzin Y, Ecemis N (2015) The use of neural networks for CPT-based liquefaction screening. Bull Eng Geol Env 74:103–116. https://doi.org/10.1007/s10064-014-0606-8
Shahri AA (2016) Assessment and prediction of liquefaction potential using different artificial neural network models: a case study. Geotech Geol Eng 34:807–815. https://doi.org/10.1007/s10706-016-0004-z
Chern S-G, Lee C-Y, Wang C-C (2008) CPT-based liquefaction assessment by using fuzzy-neural network. J Mar Sci Technol 16:139–148
Xue X, Yang X (2013) Application of the adaptive neuro-fuzzy inference system for prediction of soil liquefaction. Nat Hazards 67:901–917. https://doi.org/10.1007/s11069-013-0615-0
Kohestani VR, Hassanlourad M, Ardakani A (2015) Evaluation of liquefaction potential based on CPT data using random forest. Nat Hazards 79:1079–1089. https://doi.org/10.1007/s11069-015-1893-5
Hu JL, Tang XW, Qiu JN (2016) Assessment of seismic liquefaction potential based on Bayesian network constructed from domain knowledge and history data. Soil Dyn Earthq Eng 89:49–60. https://doi.org/10.1016/j.soildyn.2016.07.007
Hu JL, Liu HB (2019) Bayesian network models for probabilistic evaluation of earthquake-induced liquefaction based on CPT and V-s databases. Eng Geol 254:76–88. https://doi.org/10.1016/j.enggeo.2019.04.003
Young-Su K, Byung-Tak K (2006) Use of artificial neural networks in the prediction of liquefaction resistance of sands. J Geotech Geoenviron Eng 132:1502–1504. https://doi.org/10.1061/(asce)1090-0241(2006)132:11(1502)
Vapnik VN (1995) The nature of statistical learning theory. Springer, New York
Goh ATC, Goh SH (2007) Support vector machines: Their use in geotechnical engineering as illustrated using seismic liquefaction data. Comput Geotech 34:410–421. https://doi.org/10.1016/j.compgeo.2007.06.001
Khandelwal M (2010) Evaluation and prediction of blast-induced ground vibration using support vector machine. Int J Rock Mech Min Sci 47:509–516. https://doi.org/10.1016/j.ijrmms.2010.01.007
Khatibinia M, Fadaee MJ, Salajegheh J et al (2013) Seismic reliability assessment of RC structures including soil-structure interaction using wavelet weighted least squares support vector machine. Reliab Eng Syst Saf 110:22–33. https://doi.org/10.1016/j.ress.2012.09.006
Kang F, Xu Q, Li JJ (2016) Slope reliability analysis using surrogate models via new support vector machines with swarm intelligence. Appl Math Model 40:6105–6120. https://doi.org/10.1016/j.apm.2016.01.050
Zhou J, Li XB, Mitri HS (2016) Classification of Rockburst in Underground Projects: Comparison of Ten Supervised Learning Methods. J Comput Civil Eng 30. doi:https://doi.org/10.1061/(asce)cp.1943-5487.0000553
Holland JH (1975) Adaptation in natural and artificial systems. University of Michigan Press, Ann Arbor
Mirjalili S, Mirjalili SM, Lewis A (2014) Grey Wolf Optimizer Adv Eng Softw 69:46–61. https://doi.org/10.1016/j.advengsoft.2013.12.007
Muro C, Escobedo R, Spector L et al (2011) Wolf-pack (Canis lupus) hunting strategies emerge from simple rules in computational simulations. Behav Processes 88:192–197. https://doi.org/10.1016/j.beproc.2011.09.006
Xue XH, Xiao M (2016) Application of genetic algorithm-based support vector machines for prediction of soil liquefaction. Environ Earth Sci 75. doi:https://doi.org/10.1007/s12665-016-5673-7
Kayen R, Moss RES, Thompson EM et al (2013) Shear-wave velocity-based probabilistic and deterministic assessment of seismic soil liquefaction potential. J Geotech Geoenviron Eng 139:407–419. https://doi.org/10.1061/(asce)gt.1943-5606.0000743
Zhou ZY, Zhang RX, Wang YM et al (2018) Color difference classification based on optimization support vector machine of improved grey wolf algorithm. Optik 170:17–29. https://doi.org/10.1016/j.ijleo.2018.05.096
Hou KY, Shao GH, Wang HM et al (2018) Research on practical power system stability analysis algorithm based on modified SVM. Prot Control Mod Power Syst 3. doi:https://doi.org/10.1186/s41601-018-0086-0
Zhao HB (2008) Slope reliability analysis using a support vector machine. Comput Geotech 35:459–467. https://doi.org/10.1016/j.compgeo.2007.08.002
Zhou T, Lu HL, Wang WW et al (2019) GA-SVM based feature selection and parameter optimization in hospitalization expense modeling. Appl Soft Comput 75:323–332. https://doi.org/10.1016/j.asoc.2018.11.001
Yang XS (2010) A New Metaheuristic bat-inspired algorithm. In: Gonzalez JR, Pelta DA, Cruz C et al (eds) Nicso 2010: Nature inspired cooperative strategies for optimization, vol 284. Studies in computational intelligence. Springer-Verlag Berlin, Berlin, pp 65–74. doi:https://doi.org/10.1007/978-3-642-12538-6_6
Huang CL, Wang CJ (2006) A GA-based feature selection and parameters optimization for support vector machines. Expert Syst Appl 31:231–240. https://doi.org/10.1016/j.eswa.2005.09.024
Pai PF (2006) System reliability forecasting by support vector machines with genetic algorithms. Math Comput Model 43:262–274. https://doi.org/10.1016/j.mcm.2005.02.008
Tao PY, Sun Z, Sun ZX (2018) An Improved intrusion detection algorithm based on GA and SVM. IEEE Access 6:13624–13631. https://doi.org/10.1109/access.2018.2810198
Zhao M, Fu C, Ji L et al (2011) Feature selection and parameter optimization for support vector machines: a new approach based on genetic algorithm with feature chromosomes. Expert Syst Appl 38:5197–5204. https://doi.org/10.1016/j.eswa.2010.10.041
Ruan JH, Jiang H, Li XY et al (2019) A Granular GA-SVM predictor for big data in agricultural cyber-physical systems. IEEE Trans Ind Inform 15:6510–6521. https://doi.org/10.1109/tii.2019.2914158
Bian XQ, Zhang Q, Zhang L et al (2017) A grey wolf optimizer-based support vector machine for the solubility of aromatic compounds in supercritical carbon dioxide. Chem Eng Res Des 123:284–294. https://doi.org/10.1016/j.cherd.2017.05.008
Armaghani DJ, Koopialipoor M, Bahri M et al (2020) A SVR-GWO technique to minimize flyrock distance resulting from blasting. Bull Eng Geol Env 79:4369–4385. https://doi.org/10.1007/s10064-020-01834-7
Yu Z, Shi XZ, Zhou J et al (2020) Prediction of blast-induced rock movement during bench blasting: use of gray wolf optimizer and support vector regression. Nat Resour Res 29:843–865. https://doi.org/10.1007/s11053-019-09593-3
Wei Y, Ni N, Liu DY et al (2017) An Improved Grey Wolf Optimization Strategy Enhanced SVM and Its Application in Predicting the Second Major. Math Probl Eng 2017. doi:https://doi.org/10.1155/2017/9316713
Bian XQ, Zhang L, Du ZM et al (2018) Prediction of sulfur solubility in supercritical sour gases using grey wolf optimizer-based support vector machine. J Mol Liq 261:431–438. https://doi.org/10.1016/j.molliq.2018.04.070
Kaveh A, Hamze-Ziabari SM, Bakhshpoori T (2018) Patient rule-induction method for liquefaction potential assessment based on CPT data. Bull Eng Geol Env 77:849–865. https://doi.org/10.1007/s10064-016-0990-3
Rahbarzare A, Azadi M (2019) Improving prediction of soil liquefaction using hybrid optimization algorithms and a fuzzy support vector machine. Bull Eng Geol Env 78:4977–4987. https://doi.org/10.1007/s10064-018-01445-3
Fawcett T (2006) An introduction to ROC analysis. Pattern Recogn Lett 27:861–874. https://doi.org/10.1016/j.patrec.2005.10.010
Pandiyan V, Caesarendra W, Tjahjowidodo T et al (2018) In-process tool condition monitoring in compliant abrasive belt grinding process using support vector machine and genetic algorithm. J Manuf Process 31:199–213. https://doi.org/10.1016/j.jmapro.2017.11.014
Li C, Zhou J, Armaghani DJ, Cao W, Yagiz S (2021) Stochastic assessment of hard rock pillar stability based on the geological strength index system. Geomech Geophys Geo-Energy Geo-Resour 7(2):47. https://doi.org/10.1007/s40948-021-00243-8
Li E, Zhou J, Shi X, Armaghani DJ, Yu Z, Chen X, Huang P (2020) Developing a hybrid model of salp swarm algorithm-based support vector machine to predict the strength of fiber-reinforced cemented paste backfill. Eng Comput 1–22. https://doi.org/10.1007/s00366-020-01014-x
Zhou J, Qiu Y, Zhu S et al (2021) Optimization of support vector machine through the use of metaheuristic algorithms in forecasting TBM advance rate. Eng Appl Artif Intell 97:104015. https://doi.org/10.1016/j.engappai.2020.104015
Saito T, Rehmsmeier M (2015) The precision-recall plot is more informative than the ROC plot when evaluating binary classifiers on imbalanced datasets. PLoS One 10(3):e0118432. https://doi.org/10.1371/journal.pone.0118432
Zhou J, Shi XZ, Huang RD, Qiu XY, Chen C (2016) Feasibility of stochastic gradient boosting approach for predicting rockburst damage in burst-prone mines. Trans Nonferrous Metals Soc China 26(7):1938–1945
Sokolova M, Lapalme G (2009) A systematic analysis of performance measures for classification tasks. Inf Process Manage 45:427–437. https://doi.org/10.1016/j.ipm.2009.03.002
Zhou J, Shi X, Li X (2016) Utilizing gradient boosted machine for the prediction of damage to residential structures owing to blasting vibrations of open pit mining. J Vib Control 22(19):3986–3997
Acknowledgements
This research was funded by the Innovation‐Driven Project of Central South University (2020CX040) and the Shenghua Lieying Program of Central South University (Principle Investigator: Dr. Jian Zhou).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Zhou, J., Huang, S., Wang, M. et al. Performance evaluation of hybrid GA–SVM and GWO–SVM models to predict earthquake-induced liquefaction potential of soil: a multi-dataset investigation. Engineering with Computers 38 (Suppl 5), 4197–4215 (2022). https://doi.org/10.1007/s00366-021-01418-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00366-021-01418-3