Skip to main content
Springer Nature Link
Log in

An efficient technique based on cubic B-spline functions for solving time-fractional advection diffusion equation involving Atangana–Baleanu derivative

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

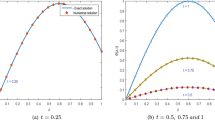
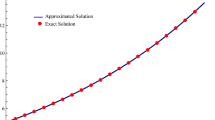
The present paper deals with cubic B-spline approximation together with \(\theta \)-weighted scheme to obtain numerical solution of the time fractional advection diffusion equation using Atangana–Baleanu derivative. To discretize the Atangana–Baleanu time derivative containing a non-singular kernel, finite difference scheme is utilized. The cubic basis functions are associated with spatial discretization. The current discretization scheme used in the present study is unconditionally stable and the convergence is of order \(O(h^2+\Delta t^{2})\). The proposed scheme is validated through some numerical examples which reveal the current scheme is feasible and quite accurate.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Diethelm K, Freed AD (1999) On the solution of nonlinear fractional-order differential equations used in the modeling of viscoplasticity. In: Scientific computing in chemical engineering II. Springer, Berlin, Heidelberg, pp 217–224

  2. Sokolov IM, Klafter J, Blumen A (2002) Fractional kinetics. Phys Today 55(11):48–54

    Article  Google Scholar 

  3. Hilfer R (ed) (2000) Applications of fractional calculus in physics, vol 35. World Scientific, Singapore

    MATH  Google Scholar 

  4. Bokhari AH, Kara AH, Zaman FD (2009) On the solutions and conservation laws of the model for tumor growth in the brain. J Math Anal Appl 350(1):256–261

    Article  MathSciNet  MATH  Google Scholar 

  5. Mainardi F (1997) Fractional calculus. In: Fractals and fractional calculus in continuum mechanics. Springer, Vienna, pp 291–348

  6. Metzler R, Klafter J (2000) The random walks guide to anomalous diffusion: a fractional dynamics approach. Phys Rep 339(1):1–77

    Article  MathSciNet  MATH  Google Scholar 

  7. Sokolov IM, Klafter J, Blumen A (2000) Ballistic versus diffusive pair dispersion in the Richardson regime. Phys Rev E 61(3):2717–2722

    Article  Google Scholar 

  8. Chen W (2006) A speculative study of 2/3-order fractional laplacian modeling of turbulence: some thoughts and conjectures. Chaos Interdiscip J Nonlinear Sci 16(2):023126

    Article  MATH  Google Scholar 

  9. Atangana A, Baleanu D (2016) New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. Therm Sci 20(2):763–769

    Article  Google Scholar 

  10. Alkahtani BST (2016) Chuas circuit model with atangana-baleanu derivative with fractional order. Chaos Solitons Fract 89:547–551

    Article  MATH  Google Scholar 

  11. Gómez-Aguilar JF (2017) Irving-mullineux oscillator via fractional derivatives with mittag-leffler kernel. Chaos Solitons Fract 95:179–186

    Article  MathSciNet  MATH  Google Scholar 

  12. Prakasha DG, Veeresha P, Baskonus HM (2019) Analysis of the dynamics of hepatitis e virus using the atangana-baleanu fractional derivative. Eur Phys J Plus 134(5):241

    Article  Google Scholar 

  13. Morales-Delgado VF, Gómez-Aguilar JF, Saad K, Escobar Jiménez RF (2019) Application of the caputo-fabrizio and atangana-baleanu fractional derivatives to mathematical model of cancer chemotherapy effect. Math Methods Appl Sci 42(4):1167–1193

    Article  MathSciNet  MATH  Google Scholar 

  14. Uçar S, Uçar E, Özdemir N, Hammouch Z (2019) Mathematical analysis and numerical simulation for a smoking model with atangana-baleanu derivative. Chaos Solitons Fract 118:300–306

    Article  MathSciNet  MATH  Google Scholar 

  15. Kumar S, Cao J, Abdel-Aty M (2020) A novel mathematical approach of covid-19 with non-singular fractional derivative. Chaos Solitons Fract 139:110048

    Article  MathSciNet  Google Scholar 

  16. Mardani A, Hooshmandasl MR, Heydari MH, Cattani C (2018) A meshless method for solving the time fractional advection-diffusion equation with variable coefficients. Comput Math Appl 75(1):122–133

    Article  MathSciNet  MATH  Google Scholar 

  17. Bu W, Liu X, Tang Y, Yang J (2015) Finite element multigrid method for multi-term time fractional advection diffusion equations. Int J Model Simul Sci Comput 6(1):1540001

    Article  Google Scholar 

  18. Sarboland M (2018) Numerical solution of time fractional partial differential equations using multiquadric quasi-interpolation scheme. Eur J Comput Mech 27(2):89–108

    Article  MathSciNet  Google Scholar 

  19. Tian W, Deng W, Wu Y (2014) Polynomial spectral collocation method for space fractional advection-diffusion equation. Numer Methods Part Differ Equ 30(2):514–535

    Article  MathSciNet  MATH  Google Scholar 

  20. Zheng Y, Li C, Zhao Z (2010) A note on the finite element method for the space-fractional advection diffusion equation. Comput Math Appl 59(5):1718–1726

    Article  MathSciNet  MATH  Google Scholar 

  21. Shen S, Liu F, Anh V (2011) Numerical approximations and solution techniques for the space-time riesz-caputo fractional advection-diffusion equation. Numer Algorithms 56(3):383–403

    Article  MathSciNet  MATH  Google Scholar 

  22. Azin H, Mohammadi F, Heydari MH (2020) A hybrid method for solving time fractional advection-diffusion equation on unbounded space domain. Adv Diff Equ 2020(1):596

    Article  MathSciNet  Google Scholar 

  23. Ahmed N, Shah NA, Vieru D (2019) Two-dimensional advection-diffusion process with memory and concentrated source. Symmetry 11(7):879

    Article  Google Scholar 

  24. Mirza IA, Vieru D (2017) Fundamental solutions to advection-diffusion equation with time-fractional caputo-fabrizio derivative. Comput Math Appl 73(1):1–10

    Article  MathSciNet  MATH  Google Scholar 

  25. Baleanu D, Agheli B, Al Qurashi MM (2016) Fractional advection differential equation within caputo and caputo-fabrizio derivatives. Adv Mech Eng 8(12):168781401668330

    Article  Google Scholar 

  26. Rubbab Q, Mirza IA, Qureshi MZA (2016) Analytical solutions to the fractional advection-diffusion equation with time-dependent pulses on the boundary. AIP Adv 6(7):075318

    Article  Google Scholar 

  27. Rubbab Q, Nazeer M, Ahmad F, Chu YM, Khan MI, Kadry S (2021) Numerical simulation of advection-diffusion equation with caputo-fabrizio time fractional derivative in cylindrical domains: applications of pseudo-spectral collocation method. Alexandria Eng J 60(1):1731–1738

    Article  Google Scholar 

  28. Korpinar Z, Inc M, Baleanu D, Bayram M (2019) Theory and application for the time fractional gardner equation with mittag-leffler kernel. J Taibah Univ Sci 13(1):813–819

    Article  Google Scholar 

  29. Owolabi KM (2018) Numerical approach to fractional blow-up equations with atangana-baleanu derivative in riemann-liouville sense. Math Model Nat Phenomena 13(1):7

    Article  MathSciNet  MATH  Google Scholar 

  30. Owolabi KM (2018) Analysis and numerical simulation of multicomponent system with atangana-baleanu fractional derivative. Chaos Solitons Fract 115:127–134

    Article  MathSciNet  MATH  Google Scholar 

  31. Kumar D, Singh J, Baleanu D (2020) On the analysis of vibration equation involving a fractional derivative with mittag-leffler law. Math Methods Appl Sci 43(1):443–457

    Article  MathSciNet  MATH  Google Scholar 

  32. Hosseininia M, Heydari MH (2019) Meshfree moving least squares method for nonlinear variable-order time fractional 2d telegraph equation involving mittag-leffler non-singular kernel. Chaos Solitons Fract 127:389–399

    Article  MathSciNet  MATH  Google Scholar 

  33. Inc M, Yusuf A, Aliyu AI, Baleanu D (2018) Investigation of the logarithmic-kdv equation involving mittag-leffler type kernel with atangana-baleanu derivative. Phys A Stat Mech Appl 506:520–531

    Article  MathSciNet  Google Scholar 

  34. Bas E, Ozarslan R (2018) Real world applications of fractional models by atangana-baleanu fractional derivative. Chaos Solitons Fract 116:121–125

    Article  MathSciNet  MATH  Google Scholar 

  35. Akgül A (2018) A novel method for a fractional derivative with non-local and non-singular kernel. Chaos Solitons Fract 114:478–482

    Article  MathSciNet  MATH  Google Scholar 

  36. Akgül A, Modanli M (2019) Crank-nicholson difference method and reproducing kernel function for third order fractional differential equations in the sense of atangana-baleanu caputo derivative. Chaos Solitons Fract 127:10–16

    Article  MathSciNet  MATH  Google Scholar 

  37. Attia N, Akgül A, Seba D, Nour A (2020) On solutions of time-fractional advection-diffusion equation. Numer Methods Part Differ Equ 1–28

  38. Yaseen M, Abbas M, Ahmad B (2021) Numerical simulation of the nonlinear generalized time-fractional klein-gordon equation using cubic trigonometric b-spline functions. Math Methods Appl Sci 44(1):901–916

    Article  MathSciNet  MATH  Google Scholar 

  39. Abbas M, Iqbal MK, Zafar B, Zin SBM (2019) New cubic b-spline approximations for solving non-linear third-order korteweg-de vries equation. Indian J Sci Technol 12(6):1–9

    Article  Google Scholar 

  40. Khalid N, Abbas M, Iqbal MK (2020) A numerical investigation of caputo time fractional allen-cahn equation using redefined cubic b-spline functions. Adv Differ Equ 158:1–22

    MathSciNet  MATH  Google Scholar 

  41. Akram T, Abbas M, Ali A (2021) A numerical study on time fractional fisher equation using an extended cubic b-spline approximation. J Math Comput Sci 22(1):85–96

    Article  Google Scholar 

  42. Akram T, Abbas M, Ismail AI, Ali NHM, Baleanu D (2019) Extended cubic b-splines in the numerical solution of time fractional telegraph equation. Adv Differ Equ 2019(1):365

    Article  MathSciNet  MATH  Google Scholar 

  43. Iqbal MK, Abbas M, Nazir T, Ali N (2020) Application of new quintic polynomial b-spline approximation for numerical investigation of kuramoto-sivashinsky equation. Adv Differ Equ 1–21:558

    Article  MathSciNet  Google Scholar 

  44. Khalid N, Abbas M, Iqbal MK, Singh J, Ismail AIM (2020) A computational approach for solving time fractional differential equation via spline functions. Alexandria Eng J 59(5):3061–3078

    Article  Google Scholar 

  45. Poulin JR (2020) Calculating infinite series using Parsevals identity (master thesis), The University of Maine, Orono

  46. Yadav S, Pandey RK, Shukla AK (2019) Numerical approximations of atangana-baleanu caputo derivative and its application. Chaos Solitons Fract 118:58–64

    Article  MathSciNet  MATH  Google Scholar 

  47. Boyce WE, Diprima RC, Meade DB (1992) Elementary differential equations and boundary value problems, vol 9. Wiley, New York

    MATH  Google Scholar 

  48. Kadalbajoo MK, Arora P (2009) B-spline collocation method for the singular-perturbation problem using artificial viscosity. Comput Math Appl 57(4):650–663

    Article  MathSciNet  MATH  Google Scholar 

  49. Hall C (1968) On error bounds for spline interpolation. J Approx Theory 1(2):209–218

    Article  MathSciNet  MATH  Google Scholar 

  50. de Boor C (1968) On the convergence of odd-degree spline interpolation. J Approx Theory 1(4):452–463

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This Research was supported by Taif University Researchers Supporting Project Number (TURSP-2020/217), Taif University, Taif, Saudi Arabia. We thank Dr. Muhammad Kashif Iqbal for his assistance in proofreading of the manuscript. The authors are also grateful to anonymous referees for their valuable suggestions, which significantly improved this manuscript.

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Sargodha, Sargodha, 40100, Pakistan

    Madiha Shafiq, Muhammad Abbas & Tahir Nazir

  2. Department of Mathematics and Statistics, College of Science, Taif University, P. O. Box 11099, Taif, 21944, Saudi Arabia

    Khadijah M. Abualnaja

  3. Department of Mathematics, Faculty of Science, Jazan University, Jazan, Saudi Arabia

    M. J. Huntul

  4. Department of Mathematics, Division of Science and Technology, University of Education, Lahore, 54770, Pakistan

    Abdul Majeed

Authors
  1. Madiha Shafiq
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Muhammad Abbas
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Khadijah M. Abualnaja
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. M. J. Huntul
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Abdul Majeed
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Tahir Nazir
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

All authors equally contributed to this work. All authors read and approved the final manuscript.

Corresponding authors

Correspondence to Madiha Shafiq, Muhammad Abbas or Khadijah M. Abualnaja.

Ethics declarations

Competing interests

The authors declare that they have no conflicts of interest to report regarding the present study.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shafiq, M., Abbas, M., Abualnaja, K.M. et al. An efficient technique based on cubic B-spline functions for solving time-fractional advection diffusion equation involving Atangana–Baleanu derivative. Engineering with Computers 38, 901–917 (2022). https://doi.org/10.1007/s00366-021-01490-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-021-01490-9

Keywords