Skip to main content
SpringerLink
Log in

Vibration of a three-phase bidirectional functionally graded sandwich beam carrying a moving mass using an enriched beam element

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

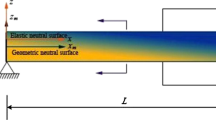
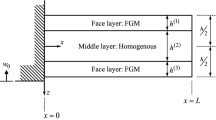
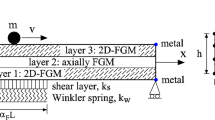
Three-phase bidirectional functionally graded sandwich (BFGSW) beams are particular type of composite beams whose properties are tailored to vary continuously in both the longitudinal and transverse directions, depending on the constituent composition distribution. These beams are known to provide superior mechanical performance and to overcome the drawbacks of the traditional sandwich beams. In this paper, a beam element is formulated for modelling free and forced vibration of a three-phase BFGSW beam carrying a moving mass. The core of the sandwich beam is homogeneous, while the two face sheets are made from power-law bidirectional functionally graded material. In addition to the Voigt micromechanical model, the Maxwell formula is used for the first time to evaluate the effective elastic moduli of the three-phase functionally graded material. The beam element based on the sinusoidal shear deformation theory is derived using hierarchical functions to enrich the conventional Lagrange and Hermite shape functions. Using the derived element, differential equations of motion for the beams are solved to obtain natural frequencies and dynamic response of the beam. The numerical result shows that the derived element is efficient, and it can yield accurate vibration characteristics with small number of elements. An extensive parametric study is carried out to highlight the effects of the material gradation, the beam geometry and velocity of the moving mass on the vibration behaviour of the beam. The influence of the micromechanical model on the vibration of the beam is also examined and discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Chakraborty A, Gopalakrishnan S, Reddy JN (2003) A new beam finite element for the analysis of functionally graded materials. Int J Mech Sci 45(3):519–539

    Article  MATH  Google Scholar 

  2. Bhangale RK, Ganesan N (2006) Thermoelastic buckling and vibration behavior of a functionally graded sandwich beam with constrained viscoelastic core. J Sound Vib 295(1–2):294–316

    Article  Google Scholar 

  3. Shahba A, Attarnejad R, Marvi MT, Hajilar S (2011) Free vibration and stability analysis of axially functionally graded tapered Timoshenko beams with classical and non-classical boundary conditions. Compos Part B-Eng 42(1):801–808

    Article  Google Scholar 

  4. Alshorbagy AE, Eltaher MA, Mahmoud FF (2011) Free vibration characteristics of a functionally graded beam by finite element method. App Math Model 35(1):412–425

    Article  MathSciNet  MATH  Google Scholar 

  5. Eltaher MA, Emam SA, Mahmoud FF (2012) Free vibration analysis of functionally graded size-dependent nanobeams. Appl Math Comput 218(14):7406–7420

    MathSciNet  MATH  Google Scholar 

  6. Eltaher MA, Alshorbagy AE, Mahmoud FF (2013) Vibration analysis of Euler-Bernoulli nanobeams by using finite element method. Appl Math Model 37(7):4787–4797

    Article  MathSciNet  Google Scholar 

  7. Taeprasartsit S (2012) Using Von Karman nonlinear displacement functions in the finite element analysis of functionally graded column. Int J Comput Methods 9(3):250042. https://doi.org/10.1142/S0219876212500429

    Article  MathSciNet  MATH  Google Scholar 

  8. Nguyen DK (2013) Large displacement response of tapered cantilever beams made of axially functionally graded material. Compos Part B-Eng 55:298–305

    Article  Google Scholar 

  9. Nguyen DK (2014) Large displacement behaviour of tapered cantilever Euler-Bernoulli beams made of functionally graded material. Appl Math Comput 237:340–355

    MathSciNet  MATH  Google Scholar 

  10. Nguyen DK, Gan BS (2014) Large deflections of tapered functionally graded beams subjected to end forces. Appl Math Model 38:3054–3066

    Article  MathSciNet  MATH  Google Scholar 

  11. Jin C, Wang X (2015) Accurate free vibration analysis of Euler functionally graded beams by the weak form quadrature element method. Compos Struct 125:41–50

    Article  Google Scholar 

  12. Kahya V, Turan M (2017) Finite element model for vibration and buckling of functionally graded beams based on the first-order shear deformation theory. Compos Part B-Eng 109:108–115

    Article  Google Scholar 

  13. Kadoli R, Akhtar K, Ganesan N (2008) Static analysis of functionally graded beams using higher order shear deformation theory. Appl Math Model 32(12):2509–2525

    Article  MATH  Google Scholar 

  14. Frikha A, Hajlaoui A, Wali M, Dammak F (2016) A new higher order C0 mixed beam element for FGM beams analysis. Compos Part B-Eng 106:181–189

    Article  Google Scholar 

  15. Vo TP, Thai HT, Nguyen TK, Maheri A, Lee J (2014) Finite element model for vibration and buckling of functionally graded sandwich beams based on a refined shear deformation theory. Eng Struct 64:12–22

    Article  Google Scholar 

  16. Vo TP, Thai HT, Nguyen TK, Inam F, Lee J (2015) A quasi-3D theory for vibration and buckling of functionally graded sandwich beams. Compos Struct 119:1–12

    Article  Google Scholar 

  17. Yarasca J, Mantari J, Arciniega R (2016) Hermite-Lagrangian finite element formulation to study functionally graded sandwich beams. Compos Struct 140:567–581

    Article  Google Scholar 

  18. Akbaş ŞD, Fageehi YA, Assie AE, Eltaher MA (2020) Dynamic analysis of viscoelastic functionally graded porous thick beams under pulse load. Eng Comput. https://doi.org/10.1007/s00366-020-01070-3

    Article  Google Scholar 

  19. Ebrahimi F, Dabbagh A (2019) Vibration analysis of graphene oxide powder-/carbon fiber-reinforced multi-scale porous nanocomposite beams: A finite-element study. Eur Phys J Plus 134:225. https://doi.org/10.1140/epjp/i2019-12594-1

    Article  Google Scholar 

  20. Dabbagh A, Rastgoo A, Ebrahimi F (2019) Finite element vibration analysis of multi-scale hybrid nanocomposite beams via a refined beam theory. Thin-Walled Struct 140:304–317

    Article  Google Scholar 

  21. Frýba L (1999) Vibration of solids and structures under moving loads. Thomas Telford, London

    Book  MATH  Google Scholar 

  22. Şimşek M, Kocatürk T (2009) Free and forced vibration of a functionally graded beam subjected to a concentrated moving harmonic load. Compos Struct 90(4):465–473

    Article  Google Scholar 

  23. Şimşek M (2010) Vibration analysis of a functionally graded beam under a moving mass by using different beam theories. Compos Struct 92(4):904–917

    Article  MathSciNet  Google Scholar 

  24. Şimşek M (2010) Non-linear vibration analysis of a functionally graded Timoshenko beam under action of a moving harmonic load. Compos Struct 92(10):2532–2546

    Article  Google Scholar 

  25. Şimşek M, Al-shujairi M (2017) Static, free and forced vibration of functionally graded (FG) sandwich beams excited by two successive moving harmonic loads. Compos Part B-Eng 108:18–34

    Article  Google Scholar 

  26. Şimşek M, Kocatürk T, Akbaş ŞD (2012) Dynamic behavior of an axially functionally graded beam under action of a moving harmonic load. Compos Struct 94(8):2358–2364

    Article  Google Scholar 

  27. Khalili SMR, Jafari AA, Eftekhari SA (2010) A mixed Ritz-DQ method for forced vibration of functionally graded beams carrying moving loads. Compos Struct 92(10):2497–2511

    Article  Google Scholar 

  28. Rajabi K, Kargarnovin MH, Gharini M (2013) Dynamic analysis of a functionally graded simply supported Euler-Bernoulli beam subjected to a moving oscillator. Acta Mech 224:425–446

    Article  MathSciNet  MATH  Google Scholar 

  29. Chen D, Yang J, Kitipornchai S (2016) Free and forced vibrations of shear deformable functionally graded porous beams. Int J Mech Sci 108–109:14–22

    Article  Google Scholar 

  30. Wang Y, Wu D (2016) Thermal effect on the dynamic response of axially functionally graded beam subjected to a moving harmonic load. Acta Astronaut 127:171–81

    Article  Google Scholar 

  31. Wang Y, Zhou A, Fu T, Zhang W (2020) Transient response of a sandwich beam with functionally graded porous core traversed by a non-uniformly distributed moving mass. Int J Mech Mater Des 16:519–540

    Article  Google Scholar 

  32. Songsuwan W, Pimsarn M, Wattanasakulpong N (2018) Dynamic responses of functionally graded sandwich beams resting on elastic foundation under harmonic moving loads. Int J Struct Stab Dyn 18(9):1850112. https://doi.org/10.1142/S0219455418501122

    Article  MathSciNet  Google Scholar 

  33. Gan BS, Trinh TH, Le TH, Nguyen DK (2015) Dynamic response of non-uniform Timoshenko beams made of axially FGM subjected to multiple moving point loads. Struct Eng Mech 53(5):981–995

    Article  Google Scholar 

  34. Esen I (2019) Dynamic response of a functionally graded Timoshenko beam on two-parameter elastic foundations due to a variable velocity moving mass. Int J Mech Sci 153–154:21–35

    Article  Google Scholar 

  35. Esen I (2019) Dynamic response of functional graded Timoshenko beams in a thermal environment subjected to an accelerating load. Eur J Mech A-Solid 78:103841. https://doi.org/10.1016/j.euromechsol.2019.103841

    Article  MathSciNet  MATH  Google Scholar 

  36. Ghatage PS, Kar VR, Sudhagar PE (2019) On the numerical modelling and analysis of multi-directional functionally graded composite structures: a review. Compos Struct 236:111837. https://doi.org/10.1016/j.compstruct.2019.111837

    Article  Google Scholar 

  37. Lezgy-Nazargah M (2015) Fully coupled thermo-mechanical analysis of bidirectional FGM beams using NURBS isogeometric finite element approach. Aerosp Sci Technol 45:154–164

    Article  Google Scholar 

  38. Şimşek M (2015) Bi-directional functionally graded materials (BDFGMs) for free and forced vibration of Timoshenko beams with various boundary conditions. Compos Struct 133:968–978

    Article  Google Scholar 

  39. Nguyen DK, Nguyen QH, Tran TT, Bui VT (2017) Vibration of bi-dimensional functionally graded Timoshenko beams excited by a moving load. Acta Mech 228:141–55

    Article  MathSciNet  MATH  Google Scholar 

  40. Nguyen DK, Vu ANT, Le NAT, Pham VN (2020) Dynamic behaviour of a bidirectional functionally graded sandwich beam under nouniform motion of a moving load. Shock Vib 2020:8854076. https://doi.org/10.1155/2020/8854076

    Article  Google Scholar 

  41. Nguyen DK, Tran TT (2018) Free vibration of tapered BFGM beams using an efficient shear deformable finite element model. Steel Compos Struct 29(3):363–377

    Google Scholar 

  42. Rajasekaran S, Khaniki HB (2019) Size-dependent forced vibration of non-uniform bi-directional functionally graded beams embedded in variable elastic environment carrying a moving harmonic mass. Appl Math Model 72:129–154

    Article  MathSciNet  MATH  Google Scholar 

  43. Attia MA, Mohamed SA (2020) Thermal vibration characteristics of pre/post-buckled bi-directional functionally graded tapered microbeams based on modified couple stress Reddy beam theory. Eng Comput. https://doi.org/10.1007/s00366-020-01188-4

  44. Vu ANT, Le NAT, Nguyen DK (2021) Dynamic behaviour of bidirectional functionally graded sandwich beams under a moving mass with partial foundation supporting effect. Acta Mech 232:2853–2875

  45. Arndt M, Machado RD, Scremin A (2010) An adaptive generalized finite element method applied to free vibration analysis of straight bars and trusses. J Sound Vib 329(6):659–672

    Article  Google Scholar 

  46. Hsu YS (2016) Enriched finite element methods for Timoshenko beam free vibration analysis. Appl Math Model 40(15–16):1–22

    MathSciNet  MATH  Google Scholar 

  47. Hsu YS, Deitos IA (2020) Enriched finite element modeling in the dynamic analysis of plane frame subject to random loads. J Mech Eng Sci 234(8):3629–3649

    Google Scholar 

  48. Le CI, Le NAT, Nguyen DK (2020) Free vibration and buckling of bidirectional functionally graded sandwich beams using an enriched third-order shear deformation beam element. Compos Struct 261:113309. https://doi.org/10.1016/j.compstruct.2020.113309

  49. Thai H-T, Vo TP (2013) A new sinusoidal shear deformation theory for bending, buckling, and vibration of functionally graded plates. App Math Model 37(5):3269–3281

    Article  MathSciNet  MATH  Google Scholar 

  50. Ebrahimi F, Nouraei M, Dabbagh A (2020) Thermal vibration analysis of embedded graphene oxide powder-reinforced nanocomposite plates. Eng Comput 36:879–895

    Article  Google Scholar 

  51. Christensen RM (1979) Mechanics of composite materials. Wiley, New York

    Google Scholar 

  52. Torquato S (2002) Random heterogeneous materials, microstructure and macroscopic properties. Springer, New York

    Book  MATH  Google Scholar 

  53. Pham DC, Tran NQ, Tran AB (2017) Polarization approximations for elastic moduli of isotropic multicomponent materials. J Mech Mater Struct 12(4):391–406

    Article  MathSciNet  Google Scholar 

  54. Nemat-Alla M, Ahmed KIE, Hassab-Allah I (2009) Elastic-plastic analysis of two-dimensional functionally graded materials under thermal loading. Int J Solids Struct 46(14–15):2774–2786

    Article  MATH  Google Scholar 

  55. Šolín P (2006) Partial differential equations and the finite element method. Wiley, Hoboken

    MATH  Google Scholar 

  56. Cook RD, Malkus DS, Plesha ME, Witt RI (2002) Concepts and applications of finite element analysis, 4th edn. Wiley, Hoboken

    Google Scholar 

  57. Praveen GN, Reddy JN (1998) Nonlinear transient thermoelastic analysis of functionally graded ceramic-metal plates. Int J Solids Struct 35(33):4457–4476

    Article  MATH  Google Scholar 

  58. Su Z, Jin G, Wang Y, Ye X (2016) A general Fourier formulation for vibration analysis of functionally graded sandwich beams with arbitrary boundary condition and resting on elastic foundations. Acta Mech 227:1493–1514

    Article  MathSciNet  MATH  Google Scholar 

  59. Song Q, Shi J, Liu Z (2017) Vibration analysis of functionally graded plate with a moving mass. Appl Math Model 46:141–160

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This research is funded by Vietnam National University Ho Chi Minh City (VNU-HCM), grant number C2020-20-13, and Vietnam Academy of Science and Technology (VAST), Grant no. NVCC03.05/21-21.

Author information

Authors and Affiliations

  1. Institute of Mechanics, VAST, 18 Hoang Quoc Viet, Hanoi, Vietnam

    Dinh Kien Nguyen

  2. Graduate University of Science and Technology, VAST, 18 Hoang Quocs Viet, Hanoi, Vietnam

    Dinh Kien Nguyen

  3. University of Transport and Communications, 3 Cau Giay, Dong Da, Hanoi, Vietnam

    An Ninh T. Vu

  4. Thuyloi University, 175 Tay Son, Dong Da, Hanoi, Vietnam

    Vu Nam Pham

  5. Faculty of Applied Science, Ho Chi Minh City University of Technology, 268 Ly Thuong Kiet Street, District 10, Ho Chi Minh City, Vietnam

    Thien Tich Truong

Authors
  1. Dinh Kien Nguyen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. An Ninh T. Vu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Vu Nam Pham
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Thien Tich Truong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dinh Kien Nguyen.

Ethics declarations

Conflict of interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nguyen, D.K., Vu, A.N.T., Pham, V.N. et al. Vibration of a three-phase bidirectional functionally graded sandwich beam carrying a moving mass using an enriched beam element. Engineering with Computers 38 (Suppl 5), 4629–4650 (2022). https://doi.org/10.1007/s00366-021-01496-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-021-01496-3

Keywords

Search

Navigation