Skip to main content
Springer Nature Link
Log in

A nonlocal strain gradient analysis of laminated composites and sandwich nanoplates using meshfree approach

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

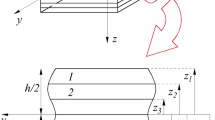
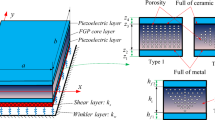
This paper aims to develop a nonlocal strain gradient meshfree plate approach which combines the nonlocal strain gradient theory (NSGT), higher order shear deformation theory (HSDT) and meshfree method, for the bending and free vibration analyses of laminated composite and sandwich nanoplates. Mechanical characteristics of small-scale structures can be described by using two scale parameters related to the nonlocal and strain gradient effects. The weak form of governing equations is extracted from the virtual work principle. Exploiting the higher order derivatives of moving Kriging (MK) shape functions, the present approach satisfies the requirement of the third-order derivatives of weak approximations. The displacements and natural frequencies of laminated composite and sandwich nanoplates are then determined by utilizing the MK meshfree method. Numerical results show that the deflections and natural frequencies of laminated composite and sandwich nanoplates are significantly influenced by the boundary conditions, nonlocal parameter and strain gradient parameter, geometry, length-to-thickness ratios. As observed, a large difference between NSGT and classical HSDT results is reported and discussed. It is clear that the results of both models coincide when the nonlocal and strain gradient parameters are taken as zero.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Wu W (2017) Inorganic nanomaterials for printed electronics: a review. Nanoscale 9(22):7342–7372

    Google Scholar 

  2. Gohardani O, Elola MC, Elizetxea C (2014) Potential and prospective implementation of carbon nanotubes on next generation aircraft and space vehicles: a review of current and expected applications in aerospace sciences. Prog Aerosp Sci 70:42–68

    Google Scholar 

  3. Bonanni A, del Valle M (2010) Use of nanomaterials for impedimetric DNA sensors: a review. Anal Chim Acta 678(1):7–17

    Google Scholar 

  4. Firoozi AA, Naji M, Dithinde M, Firoozi AA (2020) A review: influence of potential nanomaterials for civil engineering projects. Iran J Sci Technol Trans Civil Eng. https://doi.org/10.1007/s40996-020-00474-x

    Article  Google Scholar 

  5. Eringen AC (1972) Nonlocal polar elastic continua. Int J Eng Sci 10(1):1–16

    MathSciNet  MATH  Google Scholar 

  6. Mindlin RD (1965) Second gradient of strain and surface-tension in linear elasticity. Int J Solids Struct 1(4):417–438

    Google Scholar 

  7. Aifantis EC (1999) Strain gradient interpretation of size effects. Int J Fract 95(1):299

    Google Scholar 

  8. Yang F, Chong ACM, Lam DCC, Tong P (2002) Couple stress based strain gradient theory for elasticity. Int J Solids Struct 39(10):2731–2743

    MATH  Google Scholar 

  9. Lam DCC, Yang F, Chong ACM, Wang J, Tong P (2003) Experiments and theory in strain gradient elasticity. J Mech Phys Solids 51(8):1477–1508

    MATH  Google Scholar 

  10. Thai H-T, Vo TP, Nguyen T-K, Kim S-E (2017) A review of continuum mechanics models for size-dependent analysis of beams and plates. Compos Struct 177:196–219

    Google Scholar 

  11. Aifantis EC (2016) Chapter one—internal length gradient (ILG) material mechanics across scales and disciplines. In: Bordas SPA, Balint DS (eds) Advances in applied mechanics. Elsevier, Amsterdam, pp 1–110

    Google Scholar 

  12. Askes H, Aifantis EC (2011) Gradient elasticity in statics and dynamics: an overview of formulations, length scale identification procedures, finite element implementations and new results. Int J Solids Struct 48(13):1962–1990

    Google Scholar 

  13. Phung-Van P, Lieu QX, Nguyen-Xuan H, Abdel WM (2017) Size-dependent isogeometric analysis of functionally graded carbon nanotube-reinforced composite nanoplates. Compos Struct 166:120–135

    Google Scholar 

  14. Phung-Van P, Thai CH, Nguyen-Xuan H, Abdel WM (2019) Porosity-dependent nonlinear transient responses of functionally graded nanoplates using isogeometric analysis. Compos B Eng 164:215–225

    Google Scholar 

  15. Phung-Van P, Thai CH, Nguyen-Xuan H, Abdel-Wahab M (2019) An isogeometric approach of static and free vibration analyses for porous FG nanoplates. Eur J Mech A Solids 78:103851

    MathSciNet  MATH  Google Scholar 

  16. Thai CH, Ferreira AJM, Nguyen-Xuan H (2018) Isogeometric analysis of size-dependent isotropic and sandwich functionally graded microplates based on modified strain gradient elasticity theory. Compos Struct 192:274–288

    Google Scholar 

  17. Thai CH, Ferreira AJM, Phung-Van P (2020) Free vibration analysis of functionally graded anisotropic microplates using modified strain gradient theory. Eng Anal Bound Elem 117:284–298

    MathSciNet  MATH  Google Scholar 

  18. Thai CH, Ferreira AJM, Rabczuk T, Nguyen-Xuan H (2018) Size-dependent analysis of FG-CNTRC microplates based on modified strain gradient elasticity theory. Eur J Mech A Solids 72:521–538

    MathSciNet  MATH  Google Scholar 

  19. Thai CH, Ferreira AJM, Tran TD, Phung-Van P (2019) A size-dependent quasi-3D isogeometric model for functionally graded graphene platelet-reinforced composite microplates based on the modified couple stress theory. Compos Struct 234:111695

    Google Scholar 

  20. Arefi M, Mohammad-Rezaei Bidgoli E, Rabczuk T (2019) Thermo-mechanical buckling behavior of FG GNP reinforced micro plate based on MSGT. Thin Walled Struct 142:444–459

    Google Scholar 

  21. Arefi M, Mohammad-Rezaei Bidgoli E, Rabczuk T (2019) Effect of various characteristics of graphene nanoplatelets on thermal buckling behavior of FGRC micro plate based on MCST. Eur J Mech A Solids 77:103802

    MathSciNet  MATH  Google Scholar 

  22. Mohammad-Rezaei Bidgoli E, Arefi M (2019) Free vibration analysis of micro plate reinforced with functionally graded graphene nanoplatelets based on modified strain-gradient formulation. J Sandwich Struct Mater 23(2):436–472

    Google Scholar 

  23. Nguyen HX, Nguyen TN, Abdel-Wahab M, Bordas SPA, Nguyen-Xuan H, Vo TP (2017) A refined quasi-3D isogeometric analysis for functionally graded microplates based on the modified couple stress theory. Comput Methods Appl Mech Eng 313:904–940

    MathSciNet  MATH  Google Scholar 

  24. Lim CW, Zhang G, Reddy JN (2015) A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J Mech Phys Solids 78:298–313

    MathSciNet  MATH  Google Scholar 

  25. Mehralian F, Tadi Beni Y, Karimi ZM (2017) Nonlocal strain gradient theory calibration using molecular dynamics simulation based on small scale vibration of nanotubes. Phys B 514:61–69

    Google Scholar 

  26. Barretta R, Feo L, Luciano R, Marotti de Sciarra F, Penna R (2016) Functionally graded Timoshenko nanobeams: a novel nonlocal gradient formulation. Compos Part B Eng 100:208–219

    Google Scholar 

  27. Apuzzo A, Barretta R, Faghidian SA, Luciano R, Marotti de Sciarra F (2018) Free vibrations of elastic beams by modified nonlocal strain gradient theory. Int J Eng Sci 133:99–108

    MathSciNet  MATH  Google Scholar 

  28. Li L, Li X, Hu Y (2016) Free vibration analysis of nonlocal strain gradient beams made of functionally graded material. Int J Eng Sci 102:77–92

    MATH  Google Scholar 

  29. Lu L, Guo X, Zhao J (2017) A unified nonlocal strain gradient model for nanobeams and the importance of higher order terms. Int J Eng Sci 119:265–277

    Google Scholar 

  30. Ebrahimi F, Barati MR (2017) A nonlocal strain gradient refined beam model for buckling analysis of size-dependent shear-deformable curved FG nanobeams. Compos Struct 159:174–182

    Google Scholar 

  31. Farajpour A, Yazdi MRH, Rastgoo A, Mohammadi M (2016) A higher-order nonlocal strain gradient plate model for buckling of orthotropic nanoplates in thermal environment. Acta Mech 227(7):1849–1867

    MathSciNet  MATH  Google Scholar 

  32. Nematollahi MS, Mohammadi H (2019) Geometrically nonlinear vibration analysis of sandwich nanoplates based on higher-order nonlocal strain gradient theory. Int J Mech Sci 156:31–45

    Google Scholar 

  33. Arefi M, Kiani M, Rabczuk T (2019) Application of nonlocal strain gradient theory to size dependent bending analysis of a sandwich porous nanoplate integrated with piezomagnetic face-sheets. Compos B Eng 168:320–333

    Google Scholar 

  34. Arefi M, Kiani M, Zamani MH (2018) Nonlocal strain gradient theory for the magneto-electro-elastic vibration response of a porous FG-core sandwich nanoplate with piezomagnetic face sheets resting on an elastic foundation. J Sandwich Struct Mater 22(7):2157–2185

    Google Scholar 

  35. Arefi M, Mohammad-Rezaei Bidgoli E, Dimitri R, Tornabene F (2018) Free vibrations of functionally graded polymer composite nanoplates reinforced with graphene nanoplatelets. Aerosp Sci Technol 81:108–117

    Google Scholar 

  36. Mirjavadi SS, Afshari BM, Barati MR, Hamouda AMS (2019) Transient response of porous FG nanoplates subjected to various pulse loads based on nonlocal stress-strain gradient theory. Eur J Mech A Solids 74:210–220

    MathSciNet  MATH  Google Scholar 

  37. Arefi M, Zenkour A (2017) Thermo-electro-mechanical bending behavior of sandwich nanoplate integrated with piezoelectric face-sheets based on trigonometric plate theory. Compos Struct 162:108–122

    Google Scholar 

  38. Żur KK, Arefi M, Kim J, Reddy JN (2020) Free vibration and buckling analyses of magneto-electro-elastic FGM nanoplates based on nonlocal modified higher-order sinusoidal shear deformation theory. Compos Part B Eng 182:7601

    Google Scholar 

  39. Phung-Van P, Tran LV, Ferreira AJM, Nguyen-Xuan H, Abdel-Wahab M (2017) Nonlinear transient isogeometric analysis of smart piezoelectric functionally graded material plates based on generalized shear deformation theory under thermo-electro-mechanical loads. Nonlinear Dyn 87(2):879–894

    MATH  Google Scholar 

  40. Phung-Van P, Thai CH (2021) A novel size-dependent nonlocal strain gradient isogeometric model for functionally graded carbon nanotube-reinforced composite nanoplates. Eng Comput. https://doi.org/10.1007/s00366-021-01353-3

    Article  Google Scholar 

  41. Phung-Van P, Abdel-Wahab M, Liew KM, Bordas SPA, Nguyen-Xuan H (2015) Isogeometric analysis of functionally graded carbon nanotube-reinforced composite plates using higher-order shear deformation theory. Compos Struct 123:137–149

    Google Scholar 

  42. Thanh C-L, Phung-Van P, Thai CH, Nguyen-Xuan H, Abdel WM (2018) Isogeometric analysis of functionally graded carbon nanotube reinforced composite nanoplates using modified couple stress theory. Compos Struct 184:633–649

    Google Scholar 

  43. Phung-Van P, Ferreira AJM, Nguyen-Xuan H, Thai CH (2021) Scale-dependent nonlocal strain gradient isogeometric analysis of metal foam nanoscale plates with various porosity distributions. Compos Struct 268:113949

    Google Scholar 

  44. Thai CH, Nguyen LB, Nguyen-Xuan H, Phung-Van P (2021) Size-dependent nonlocal strain gradient modeling of hexagonal beryllium crystal nanoplates. Int J Mech Mater Design. https://doi.org/10.1007/s10999-021-09561-x

    Article  Google Scholar 

  45. Fan F, Safaei B, Sahmani S (2020) Buckling and postbuckling response of nonlocal strain gradient porous functionally graded micro/nano-plates via NURBS-based isogeometric analysis. Thin-Walled Struct 159:107231

    Google Scholar 

  46. Fan F, Sahmani S, Safaei B (2021) Isogeometric nonlinear oscillations of nonlocal strain gradient PFGM micro/nano-plates via NURBS-based formulation. Compos Struct 255:112969

    Google Scholar 

  47. Jalaei MH, Thai H-T (2019) Dynamic stability of viscoelastic porous FG nanoplate under longitudinal magnetic field via a nonlocal strain gradient quasi-3D theory. Compos Part B Eng 175:107164

    Google Scholar 

  48. Sahmani S, Fattahi AM (2018) Small scale effects on buckling and postbuckling behaviors of axially loaded FGM nanoshells based on nonlocal strain gradient elasticity theory. Appl Math Mech 39(4):561–580

    MathSciNet  MATH  Google Scholar 

  49. Ghorbani K, Mohammadi K, Rajabpour A, Ghadiri M (2019) Surface and size-dependent effects on the free vibration analysis of cylindrical shell based on Gurtin-Murdoch and nonlocal strain gradient theories. J Phys Chem Solids 129:140–150

    Google Scholar 

  50. Cornacchia F, Fantuzzi N, Luciano R, Penna R (2019) Solution for cross- and angle-ply laminated Kirchhoff nano plates in bending using strain gradient theory. Compos Part B Eng 173:7006

    Google Scholar 

  51. Bacciocchi M, Fantuzzi N, Ferreira AJM (2020) Conforming and nonconforming laminated finite element Kirchhoff nanoplates in bending using strain gradient theory. Comput Struct 239:6322

    Google Scholar 

  52. Raghu P, Rajagopal A, Reddy JN (2018) Nonlocal nonlinear finite element analysis of composite plates using TSDT. Compos Struct 185:38–50

    Google Scholar 

  53. Gu L (2003) Moving kriging interpolation and element-free Galerkin method. Int J Numer Methods Eng 56(1):1–11

    MATH  Google Scholar 

  54. Thai CH, Do VNV, Nguyen-Xuan H (2016) An improved Moving Kriging-based meshfree method for static, dynamic and buckling analyses of functionally graded isotropic and sandwich plates. Eng Anal Bound Elem 64:122–136

    MathSciNet  MATH  Google Scholar 

  55. Nguyen TN, Thai CH, Nguyen-Xuan H (2016) A novel computational approach for functionally graded isotropic and sandwich plate structures based on a rotation-free meshfree method. Thin Walled Struct 107:473–488

    Google Scholar 

  56. Thai CH, Nguyen TN, Rabczuk T, Nguyen-Xuan H (2016) An improved moving Kriging meshfree method for plate analysis using a refined plate theory. Comput Struct 176:34–49

    Google Scholar 

  57. Thai CH, Tran TD, Phung-van P (2020) A size-dependent moving Kriging meshfree model for deformation and free vibration analysis of functionally graded carbon nanotube-reinforced composite nanoplates. Eng Anal Bound Elem 115:52–63

    MathSciNet  MATH  Google Scholar 

  58. Thai CH, Ferreira A, Lee J, Nguyen-Xuan H (2018) An efficient size-dependent computational approach for functionally graded isotropic and sandwich microplates based on modified couple stress theory and moving Kriging-based meshfree method. Int J Mech Sci 142:322–338

    Google Scholar 

  59. Thai CH, Ferreira AJM, Nguyen-Xuan H (2017) Naturally stabilized nodal integration meshfree formulations for analysis of laminated composite and sandwich plates. Compos Struct 178:260–276

    Google Scholar 

  60. Thai CH, Ferreira AJM, Rabczuk T, Nguyen-Xuan H (2018) A naturally stabilized nodal integration meshfree formulation for carbon nanotube-reinforced composite plate analysis. Eng Anal Bound Elem 92:136–155

    MathSciNet  MATH  Google Scholar 

  61. Thai CH, Ferreira AJM, Wahab MA, Nguyen-Xuan H (2018) A moving Kriging meshfree method with naturally stabilized nodal integration for analysis of functionally graded material sandwich plates. Acta Mech 229(7):2997–3023

    MathSciNet  MATH  Google Scholar 

  62. Thai CH, Phung-Van P (2020) A meshfree approach using naturally stabilized nodal integration for multilayer FG GPLRC complicated plate structures. Eng Anal Bound Elem 117:346–358

    MathSciNet  MATH  Google Scholar 

  63. Thai CH, Ferreira AJM, Phung-Van P (2020) A nonlocal strain gradient isogeometric model for free vibration and bending analyses of functionally graded plates. Compos Struct 251:112634

    Google Scholar 

  64. Thai CH, Ferreira AJM, Nguyen-Xuan H, Phung-Van P (2021) A size dependent meshfree model for functionally graded plates based on the nonlocal strain gradient theory. Compos Struct 272:114169

    Google Scholar 

  65. Reddy JN (1984) A simple higher-order theory for laminated composite plates. J Appl Mech 51(4):745–752

    MATH  Google Scholar 

  66. Pagano NJ (1970) Exact solutions for rectangular bidirectional composites and sandwich plates. J Compos Mater 4(1):20–34

    Google Scholar 

  67. Srinivas S (1973) A refined analysis of composite laminates. J Sound Vib 30(4):495–507

    MATH  Google Scholar 

  68. Ferreira AJM, Fasshauer GE, Batra RC, Rodrigues JD (2008) Static deformations and vibration analysis of composite and sandwich plates using a layerwise theory and RBF-PS discretizations with optimal shape parameter. Compos Struct 86(4):328–343

    Google Scholar 

  69. Liew KM, Huang YQ, Reddy JN (2003) Vibration analysis of symmetrically laminated plates based on FSDT using the moving least squares differential quadrature method. Comput Methods Appl Mech Eng 192(19):2203–2222

    MATH  Google Scholar 

  70. Ferreira AJM, Castro LMS, Bertoluzza S (2009) A high order collocation method for the static and vibration analysis of composite plates using a first-order theory. Compos Struct 89(3):424–432

    Google Scholar 

Download references

Acknowledgements

This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 107.02-2019.35.

Author information

Authors and Affiliations

  1. Division of Computational Mechanics, Ton Duc Thang University, Ho Chi Minh City, Vietnam

    Chien H. Thai

  2. Faculty of Civil Engineering, Ton Duc Thang University, Ho Chi Minh City, Vietnam

    Chien H. Thai

  3. Departamento de Engenharia Mecanica, Faculdade de Engenharia, Universidade Do Porto, Rua Dr. Roberto Frias, 4200-465, Porto, Portugal

    A. J. M. Ferreira

  4. CIRTECH Institute, Ho Chi Minh City University of Technology (HUTECH), Ho Chi Minh City, Vietnam

    H. Nguyen-Xuan

  5. Department of Architectural Engineering, Sejong University, 209 Neungdong-ro, Gwangjin-gu, Seoul, 05006, Republic of Korea

    H. Nguyen-Xuan

  6. Faculty of Civil Engineering, Ho Chi Minh City University of Technology and Education (HCMUTE), Ho Chi Minh City, Vietnam

    Lieu B. Nguyen

  7. Faculty of Civil Engineering, Ho Chi Minh City University of Technology (HUTECH), Ho Chi Minh City, Vietnam

    P. Phung-Van

Authors
  1. Chien H. Thai
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. A. J. M. Ferreira
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. H. Nguyen-Xuan
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Lieu B. Nguyen
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. P. Phung-Van
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding authors

Correspondence to Chien H. Thai or P. Phung-Van.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Thai, C.H., Ferreira, A.J.M., Nguyen-Xuan, H. et al. A nonlocal strain gradient analysis of laminated composites and sandwich nanoplates using meshfree approach. Engineering with Computers 39, 5–21 (2023). https://doi.org/10.1007/s00366-021-01501-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-021-01501-9

Keywords