Skip to main content

Advertisement

Springer Nature Link
Log in

A hybrid approach for interval prediction of concrete dam displacements under uncertain conditions

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

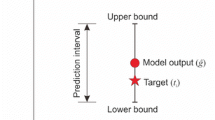
Accurate and credible displacement prediction is essential to dam safety monitoring. However, due to the inherent uncertainties involved in dam systems, errors of conventional deterministic point predictions are inevitable and sometimes large. In this paper, prediction intervals (PIs) are used instead of deterministic values to quantify the associated uncertainties and improve the reliability of dam displacement prediction. A hybrid modeling approach is proposed to synthetically evaluate the aleatoric and epistemic uncertainties through PI construction, which integrates the non-parametric bootstrap, least squares support vector machine (LSSVM), and artificial neural network (ANN) algorithms. Specifically, the PIs of dam displacement are constructed in two stages. In the first stage, multiple bootstrap-based LSSVMs are utilized to estimate the true regression means of future displacements and the variance of model uncertainty. In the second stage, a modified ANN (MANN) is developed and applied to estimate the variance of data noise. The final PIs are calculated by combining the true regression means and the variances of model uncertainty and data noise. The performance of the bootstrap-LSSVM–MANN model is verified using monitoring data from a real concrete dam. The results show that the proposed method can generate computationally efficient high-quality PIs and can effectively deal with multiple uncertainties in data-driven modeling and prediction. The novel approach has great potential to support the decision-making activities in an environment characterized by uncertainties and risks.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Prakash G, Sadhu A, Narasimhan S et al (2018) Initial service life data towards structural health monitoring of a concrete arch dam. Struct Control Health Monit 25(1):e2036

    Google Scholar 

  2. Wei BW, Chen LJ, Li HK et al (2020) Optimized prediction model for concrete dam displacement based on signal residual amendment. Appl Math Model 78:20–36

    MathSciNet  MATH  Google Scholar 

  3. Ranković V, Grujović N, Divac D et al (2014) Development of support vector regression identification model for prediction of dam structural behaviour. Struct Saf 48:33–39

    Google Scholar 

  4. Li MC, Shen Y, Ren QB et al (2019) A new distributed time series evolution prediction model for dam deformation based on constituent elements. Adv Eng Inform 39:41–52

    Google Scholar 

  5. Su HZ, Wen ZP, Chen ZX et al (2016) Dam safety prediction model considering chaotic characteristics in prototype monitoring data series. Struct Health Monit 15(6):639–649

    Google Scholar 

  6. Lin CN, Li TC, Chen SY et al (2019) Gaussian process regression-based forecasting model of dam deformation. Neural Comput Appl 31(12):8503–8518

    Google Scholar 

  7. Lin CN, Li TC, Chen SY et al (2020) Structural identification in long-term deformation characteristic of dam foundation using meta-heuristic optimization techniques. Adv Eng Softw 148:102870

    Google Scholar 

  8. Wei BW, Yuan DY, Xu ZK et al (2018) Modified hybrid forecast model considering chaotic residual errors for dam deformation. Struct Control Health Monit 25(8):e2188

    Google Scholar 

  9. Li B, Yang J, Hu DX (2020) Dam monitoring data analysis methods: a literature review. Struct Control Health Monit 27(3):e2501

    Google Scholar 

  10. Wang SW, Xu C, Gu CS et al (2020) Displacement monitoring model of concrete dams using the shape feature clustering-based temperature principal component factor. Struct Control Health Monit 27(10):e2603

    Google Scholar 

  11. Ren QB, Li MC, Song LG et al (2020) An optimized combination prediction model for concrete dam deformation considering quantitative evaluation and hysteresis correction. Adv Eng Inform 46:101154

    Google Scholar 

  12. Kang F, Liu X, Li JJ (2020) Temperature effect modeling in structural health monitoring of concrete dams using kernel extreme learning machines. Struct Health Monit 19(4):987–1002

    Google Scholar 

  13. Hu J, Wu SH (2019) Statistical modeling for deformation analysis of concrete arch dams with influential horizontal cracks. Struct Health Monit 18(2):546–562

    Google Scholar 

  14. Wang SW, Xu YL, Gu CS et al (2019) Hysteretic effect considered monitoring model for interpreting abnormal deformation behavior of arch dams: a case study. Struct Control Health Monit 26(10):e2417

    Google Scholar 

  15. Dai B, Gu CS, Zhao EF et al (2018) Statistical model optimized random forest regression model for concrete dam deformation monitoring. Struct Control Health Monit 25(6):e2170

    Google Scholar 

  16. Kao CY, Loh CH (2013) Monitoring of long-term static deformation data of Fei-Tsui arch dam using artificial neural network-based approaches. Struct Control Health Monit 20(3):282–303

    Google Scholar 

  17. Kang F, Li JJ, Zhao SZ et al (2019) Structural health monitoring of concrete dams using long-term air temperature for thermal effect simulation. Eng Struct 180:642–653

    Google Scholar 

  18. Tabari MMR, Sanayei HRZ (2019) Prediction of the intermediate block displacement of the dam crest using artificial neural network and support vector regression models. Soft Comput 23(19):9629–9645

    Google Scholar 

  19. Cheng L, Zheng DJ (2013) Two online dam safety monitoring models based on the process of extracting environmental effect. Adv Eng Softw 57:48–56

    Google Scholar 

  20. Su HZ, Wen ZP, Sun XR et al (2015) Time-varying identification model for dam behavior considering structural reinforcement. Struct Saf 57:1–7

    Google Scholar 

  21. Su HZ, Chen ZX, Wen ZP (2016) Performance improvement method of support vector machine-based model monitoring dam safety. Struct Control Health Monit 23(2):252–266

    Google Scholar 

  22. Kang F, Liu J, Li JJ et al (2017) Concrete dam deformation prediction model for health monitoring based on extreme learning machine. Struct Control Health Monit 24(10):e1997

    Google Scholar 

  23. Chen SY, Gu CS, Lin CN et al (2020) Prediction, monitoring, and interpretation of dam leakage flow via adaptative kernel extreme learning machine. Measurement 166:108161

    Google Scholar 

  24. Wang XL, Xie HY, Wang JJ et al (2020) Prediction of dam deformation based on Bootstrap and ICS-MKELM algorithm. J Hydroelectr Eng 39(3):106–120 (in Chinese)

    Google Scholar 

  25. Li X, Wen ZP, Su HZ (2019) An approach using random forest intelligent algorithm to construct a monitoring model for dam safety. Eng Comput 3:1–18. https://doi.org/10.1007/s00366-019-00806-0

    Article  Google Scholar 

  26. Su HZ, Li X, Yang BB et al (2018) Wavelet support vector machine-based prediction model of dam deformation. Mech Syst Signal Process 110:412–427

    Google Scholar 

  27. Kang F, Li JJ, Dai JH (2019) Prediction of long-term temperature effect in structural health monitoring of concrete dams using support vector machines with Jaya optimizer and salp swarm algorithms. Adv Eng Softw 131:60–76

    Google Scholar 

  28. Luo XG, Yuan XH, Zhu S et al (2019) A hybrid support vector regression framework for streamflow forecast. J Hydrol 568:184–193

    Google Scholar 

  29. Zhou J, Li XB, Shi XZ (2012) Long-term prediction model of rockburst in underground openings using heuristic algorithms and support vector machines. Saf Sci 50(4):629–644

    Google Scholar 

  30. Yan WW, Shao HH (2003) Application of support vector machines and least squares support vector machines to heart disease diagnoses. Control Decis 3:358–360 (in Chinese)

    Google Scholar 

  31. Chen SY, Gu CS, Lin CN et al (2020) Multi-kernel optimized relevance vector machine for probabilistic prediction of concrete dam displacement. Eng Comput. https://doi.org/10.1007/s00366-019-00924-9

    Article  Google Scholar 

  32. Hariri-Ardebili MA, Salazar F (2020) Engaging soft computing in material and modeling uncertainty quantification of dam engineering problems. Soft Comput 24(15):11583–11604

    Google Scholar 

  33. Nourani V, Sayyah-Fard M, Alami MT et al (2020) Data pre-processing effect on ANN-based prediction intervals construction of the evaporation process at different climate regions in Iran. J Hydrol 588:125078

    Google Scholar 

  34. Li KW, Wang R, Lei HT et al (2018) Interval prediction of solar power using an improved Bootstrap method. Sol Energy 159:97–112

    Google Scholar 

  35. Nourani V, Paknezhad NJ, Sharghi E et al (2019) Estimation of prediction interval in ANN-based multi-GCMs downscaling of hydro-climatologic parameters. J Hydrol 579:124226

    Google Scholar 

  36. Wan C, Xu Z, Pinson P et al (2013) Probabilistic forecasting of wind power generation using extreme learning machine. IEEE Trans Power Syst 29(3):1033–1044

    Google Scholar 

  37. Khosravi A, Nahavandi S, Creighton D et al (2011) Comprehensive review of neural network-based prediction intervals and new advances. IEEE Trans Neural Netw 22(9):1341–1356

    Google Scholar 

  38. Freedman DA (1981) Bootstrapping regression models. Ann Stat 9(6):1218–1228

    MathSciNet  MATH  Google Scholar 

  39. Flachaire E (2005) Bootstrapping heteroskedastic regression models: wild bootstrap vs. pairs bootstrap. Comput Stat Data Anal 49(2):361–376

    MathSciNet  MATH  Google Scholar 

  40. Suykens JAK, Vandewalle J (1999) Least squares support vector machine classifiers. Neural Process Lett 9(3):293–300

    Google Scholar 

  41. Cheng MY, Prayogo D, Wu YW (2019) Prediction of permanent deformation in asphalt pavements using a novel symbiotic organisms search-least squares support vector regression. Neural Comput Appl 31(10):6261–6273

    Google Scholar 

  42. Chou JS, Ngo NT, Pham AD (2016) Shear strength prediction in reinforced concrete deep beams using nature-inspired metaheuristic support vector regression. J Comput Civ Eng 30(1):04015002

    Google Scholar 

  43. Wan C, Xu Z, Wang YL et al (2013) A hybrid approach for probabilistic forecasting of electricity price. IEEE Trans Smart Grid 5(1):463–470

    Google Scholar 

  44. Zio E (2006) A study of the bootstrap method for estimating the accuracy of artificial neural networks in predicting nuclear transient processes. IEEE Trans Nucl Sci 53(3):1460–1478

    Google Scholar 

  45. Ren QB, Li MC, Du SL et al (2019) Mathematical model and practical formula for indirect determination of shear strength of dam rockfill materials. J Hydraul Eng 50(10):1200–1213 (in Chinese)

    Google Scholar 

Download references

Acknowledgements

This research was jointly funded by the National Natural Science Foundation of China (Grant no. 51879185), the National Key Research and Development Program (Grant no. 2018YFC0406905) and the Open Fund of Hubei Key Laboratory of Construction and Management in Hydropower Engineering (Grant no. 2020KSD06).

Author information

Authors and Affiliations

  1. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin, 300350, China

    Qiubing Ren & Mingchao Li

  2. Northwest Engineering Corporation Limited, Power China, Xi’an, 710065, China

    Rui Kong

  3. China Three Gorges Corporation, Beijing, 100038, China

    Yang Shen

  4. Bei Fang Investigation, Design and Research CO. LTD, Tianjin, 300222, China

    Shengli Du

Authors
  1. Qiubing Ren
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Mingchao Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Rui Kong
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Yang Shen
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Shengli Du
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Mingchao Li.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ren, Q., Li, M., Kong, R. et al. A hybrid approach for interval prediction of concrete dam displacements under uncertain conditions. Engineering with Computers 39, 1285–1303 (2023). https://doi.org/10.1007/s00366-021-01515-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-021-01515-3

Keywords