Skip to main content
SpringerLink
Log in

Free vibration analysis of nanoplates with auxetic honeycomb core using a new third-order finite element method and nonlocal elasticity theory

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

This paper proposes a finite element method (FEM) for the free vibration analysis of sandwich nanoplates with an auxetic honeycomb core. The proposed method uses a third-order shear deformation theory accounting for both shear deformation and stretching effects without any need for shear correction factors. The size-dependent effect is solved using the nonlocal elasticity theory. The auxetic sandwich nanoplate with negative Poisson’s ratio is applied to achieve ultra-light features and high strength. The obtained numerical results by the proposed method are compared with other published works to demonstrate the accuracy and reliability. Moreover, the influence of the nonlocal factor, geometrics parameters, and material properties (especially the auxetic honeycomb parameters) on the free vibration behavior of sandwich nanoplates is also examined in the numerical examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

(source: internet)

Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Data Availability

The data used to support the findings of this study are included within the article.

References

  1. Eringen AC (1983) On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys 54:4703–4710

    Google Scholar 

  2. Liu Y, Zhou J, Hui D (2012) A strain-gradient plasticity theory of bimodal nanocrystalline materials with composite structure. Compos B Eng 43:249–254

    Google Scholar 

  3. Yang F, Chong A, Lam DCC, Tong P (2002) Couple stress based strain gradient theory for elasticity. Int J Solids Struct 39:2731–2743

    MATH  Google Scholar 

  4. Eringen AC, Wegner J (2003) Nonlocal continuum field theories. Appl Mech Rev 56:B20–B22

    Google Scholar 

  5. Aifantis EC (1999) Strain gradient interpretation of size effects. Fracture scaling. Springer, pp 299–314.

  6. Aifantis EC (2003) Update on a class of gradient theories. Mech Mater 35:259–280

    Google Scholar 

  7. Aifantis EC (2011) On the gradient approach–relation to Eringen’s nonlocal theory. Int J Eng Sci 49:1367–1377

    MathSciNet  Google Scholar 

  8. Peddieson J, Buchanan GR, McNitt RP (2003) Application of nonlocal continuum models to nanotechnology. Int J Eng Sci 41:305–312

    Google Scholar 

  9. Reddy J (2007) Nonlocal theories for bending, buckling and vibration of beams. Int J Eng Sci 45:288–307

    MATH  Google Scholar 

  10. Reddy J (2010) Nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates. Int J Eng Sci 48:1507–1518

    MathSciNet  MATH  Google Scholar 

  11. Aydogdu M (2009) A general nonlocal beam theory: its application to nanobeam bending, buckling and vibration. Physica E 41:1651–1655

    Google Scholar 

  12. Wang C, Kitipornchai S, Lim C, Eisenberger M (2008) Beam bending solutions based on nonlocal Timoshenko beam theory. J Eng Mech 134:475–481

    Google Scholar 

  13. Pradhan S (2012) Nonlocal finite element analysis and small scale effects of CNTs with Timoshenko beam theory. Finite Elem Anal Des 50:8–20

    Google Scholar 

  14. Ghannadpour S, Mohammadi B, Fazilati J (2013) Bending, buckling and vibration problems of nonlocal Euler beams using Ritz method. Compos Struct 96:584–589

    Google Scholar 

  15. Ke L-L, Xiang Y, Yang J, Kitipornchai S (2009) Nonlinear free vibration of embedded double-walled carbon nanotubes based on nonlocal Timoshenko beam theory. Comput Mater Sci 47:409–417

    Google Scholar 

  16. Ansari R, Sahmani S, Arash B (2010) Nonlocal plate model for free vibrations of single-layered graphene sheets. Phys Lett A 375:53–62

    Google Scholar 

  17. Hosseini-Hashemi S, Zare M, Nazemnezhad R (2013) An exact analytical approach for free vibration of Mindlin rectangular nano-plates via nonlocal elasticity. Compos Struct 100:290–299

    Google Scholar 

  18. Malekzadeh P, Setoodeh A, Beni AA (2011) Small scale effect on the free vibration of orthotropic arbitrary straight-sided quadrilateral nanoplates. Compos Struct 93:1631–1639

    Google Scholar 

  19. Mohammadi M, Goodarzi M, Ghayour M, Farajpour A (2013) Influence of in-plane pre-load on the vibration frequency of circular graphene sheet via nonlocal continuum theory. Compos B Eng 51:121–129

    Google Scholar 

  20. Mohammadi M, Ghayour M, Farajpour A (2013) Free transverse vibration analysis of circular and annular graphene sheets with various boundary conditions using the nonlocal continuum plate model. Compos B Eng 45:32–42

    Google Scholar 

  21. Pradhan S, Kumar A (2011) Vibration analysis of orthotropic graphene sheets using nonlocal elasticity theory and differential quadrature method. Compos Struct 93:774–779

    Google Scholar 

  22. Daikh AA, Drai A, Bensaid I, Houari MSA, Tounsi A (2020) On vibration of functionally graded sandwich nanoplates in the thermal environment. J Sandw Struct Mater. https://doi.org/10.1177/1099636220909790

    Article  Google Scholar 

  23. Vu-Bac N, Duong T, Lahmer T, Areias P, Sauer R, Park H, Rabczuk T (2019) A NURBS-based inverse analysis of thermal expansion induced morphing of thin shells. Comput Methods Appl Mech Eng 350:480–510

    MathSciNet  MATH  Google Scholar 

  24. Shen L, Shen H-S, Zhang C-L (2010) Nonlocal plate model for nonlinear vibration of single layer graphene sheets in thermal environments. Comput Mater Sci 48:680–685

    Google Scholar 

  25. Shen H-S (2011) Nonlocal plate model for nonlinear analysis of thin films on elastic foundations in thermal environments. Compos Struct 93:1143–1152

    Google Scholar 

  26. Murmu T, Pradhan S (2009) Vibration analysis of nanoplates under uniaxial prestressed conditions via nonlocal elasticity. J Appl Phys 106:104301

    Google Scholar 

  27. Thang PT, Tran P, Nguyen-Thoi T (2021) Applying nonlocal strain gradient theory to size-dependent analysis of functionally graded carbon nanotube-reinforced composite nanoplates. Appl Math Model 93:775–791

    MathSciNet  MATH  Google Scholar 

  28. Thang PT, Nguyen-Thoi T, Lee J (2021) Modeling and analysis of bi-directional functionally graded nanobeams based on nonlocal strain gradient theory. Appl Math Comput 407:126303

    MathSciNet  MATH  Google Scholar 

  29. Tran V-K, Tran T-T, Phung M-V, Pham Q-H, Nguyen-Thoi T (2020) A finite element formulation and nonlocal theory for the static and free vibration analysis of the sandwich functionally graded nanoplates resting on elastic foundation. J Nanomat 2020.

  30. Pham Q-H, Tran TT, Tran VK, Nguyen P-C, Nguyen-Thoi T (2021) Free vibration of functionally graded porous non-uniform thickness annular-nanoplates resting on elastic foundation using ES-MITC3 element. Alexand Eng J

  31. Doan TL, Le PB, Tran TT, Trai VK, Pham QH (2021) Free vibration analysis of functionally graded porous nano-plates with different shapes resting on elastic foundation. J Appl Comput Mech 7(3):1593–1605

    Google Scholar 

  32. Tran TT, Tran VK, Pham Q-H, Zenkour AM (2021) Extended four-unknown higher-order shear deformation nonlocal theory for bending, buckling and free vibration of functionally graded porous nanoshell resting on elastic foundation. Compos Struct 264:113737

    Google Scholar 

  33. Lu G, Yu T (2003) Energy absorption of structures and materials. Elsevier

    Google Scholar 

  34. Lim T-C (2015) Auxetic materials and structures. Springer

    Google Scholar 

  35. Ren X, Das R, Tran P, Ngo TD, Xie YM (2018) Auxetic metamaterials and structures: a review. Smart Mater Struct 27:023001

    Google Scholar 

  36. Wan H, Ohtaki H, Kotosaka S, Hu G (2004) A study of negative Poisson’s ratios in auxetic honeycombs based on a large deflection model. Eur J Mech A/Sol 23:95–106

    MATH  Google Scholar 

  37. Zhu X, Zhang J, Zhang W, Chen J (2019) Vibration frequencies and energies of an auxetic honeycomb sandwich plate. Mech Adv Mater Struct 26:1951–1957

    Google Scholar 

  38. Vu-Bac N, Duong TX, Lahmer T, Zhuang X, Sauer RA, Park H, Rabczuk T (2018) A NURBS-based inverse analysis for reconstruction of nonlinear deformations of thin shell structures. Comput Methods Appl Mech Eng 331:427–455

    MathSciNet  MATH  Google Scholar 

  39. Zhang X-C, An L-Q, Ding H-M, Zhu X-Y, El-Rich M (2015) The influence of cell micro-structure on the in-plane dynamic crushing of honeycombs with negative Poisson’s ratio. J Sandw Struct Mater 17:26–55

    Google Scholar 

  40. Nguyen DD, Pham CH (2018) Nonlinear dynamic response and vibration of sandwich composite plates with negative Poisson’s ratio in auxetic honeycombs. J Sandw Struct Mater 20:692–717

    Google Scholar 

  41. Duc ND, Seung-Eock K, Cong PH, Anh NT, Khoa ND (2017) Dynamic response and vibration of composite double curved shallow shells with negative Poisson’s ratio in auxetic honeycombs core layer on elastic foundations subjected to blast and damping loads. Int J Mech Sci 133:504–512

    Google Scholar 

  42. Nguyen NV, Nguyen-Xuan H, Nguyen TN, Kang J, Lee J (2021) A comprehensive analysis of auxetic honeycomb sandwich plates with graphene nanoplatelets reinforcement. Compos Struct 259:113213

    Google Scholar 

  43. Cong PH, Long PT, Van Nhat N, Duc ND (2019) Geometrically nonlinear dynamic response of eccentrically stiffened circular cylindrical shells with negative poisson’s ratio in auxetic honeycombs core layer. Int J Mech Sci 152:443–453

    Google Scholar 

  44. Cong PH, Khanh ND, Khoa ND, Duc ND (2018) New approach to investigate nonlinear dynamic response of sandwich auxetic double curves shallow shells using TSDT. Compos Struct 185:455–465

    Google Scholar 

  45. Tran TT, Pham QH, Nguyen-Thoi T (2020) Dynamic analysis of sandwich auxetic honeycomb plates subjected to moving oscillator load on elastic foundation. Adv Mater Sci Eng. https://doi.org/10.1155/2020/6309130

    Article  Google Scholar 

  46. Jha D, Kant T, Singh R (2013) A critical review of recent research on functionally graded plates. Compos Struct 96:833–849

    Google Scholar 

  47. Thai H-T, Kim S-E (2015) A review of theories for the modeling and analysis of functionally graded plates and shells. Compos Struct 128:70–86

    Google Scholar 

  48. Shi G (2007) A new simple third-order shear deformation theory of plates. Int J Sol Struct 44:4399–4417

    MATH  Google Scholar 

  49. Wattanasakulpong N, Prusty BG, Kelly DW (2011) Thermal buckling and elastic vibration of third-order shear deformable functionally graded beams. Int J Mech Sci 53:734–743

    Google Scholar 

  50. Wattanasakulpong N, Prusty GB, Kelly DW (2013) Free and forced vibration analysis using improved third-order shear deformation theory for functionally graded plates under high temperature loading. J Sandw Struct Mater 15:583–606

    Google Scholar 

  51. Bui TQ, Van Do T, Ton LHT, Doan DH, Tanaka S, Pham DT, Nguyen-Van T-A, Yu T, Hirose S (2016) On the high temperature mechanical behaviors analysis of heated functionally graded plates using FEM and a new third-order shear deformation plate theory. Compos B Eng 92:218–241

    Google Scholar 

  52. Van Do T, Nguyen DK, Duc ND, Doan DH, Bui TQ (2017) Analysis of bi-directional functionally graded plates by FEM and a new third-order shear deformation plate theory. Thin Wall Struct 119:687–699

    Google Scholar 

  53. Reddy JN (2006) Theory and analysis of elastic plates and shells. CRC Press

    Google Scholar 

  54. Belkorissat I, Houari MSA, Tounsi A, Bedia E, Mahmoud S (2015) On vibration properties of functionally graded nano-plate using a new nonlocal refined four variable model. Steel Compos Struct 18:1063–1081

    Google Scholar 

  55. Aghababaei R, Reddy J (2009) Nonlocal third-order shear deformation plate theory with application to bending and vibration of plates. J Sound Vib 326:277–289

    Google Scholar 

  56. Sobhy M, Radwan AF (2017) A new quasi 3D nonlocal plate theory for vibration and buckling of FGM nanoplates. Int J Appl Mech 9:1750008

    Google Scholar 

  57. Vinyas M, Da H, Nguyen-Thoi T (2020) Influence of active constrained layer damping on the coupled vibration response of functionally graded magneto-electro-elastic plates with skewed edges. Defence Technol 16:1019–1038

    Google Scholar 

  58. HS NK, Kattimani S, Nguyen-Thoi T (2021) Influence of porosity distribution on nonlinear free vibration and transient responses of porous functionally graded skew plates. Defence Technology.

  59. Srinivasa C, Suresh Y, Kumar WP (2012) Buckling studies on laminated composite skew plates. Int J Comput Appl 37:35–47

    Google Scholar 

Download references

Acknowledgements

This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under Grant number 107.02-2019.330.

Author information

Authors and Affiliations

  1. Advanced Structural Engineering Laboratory, Faculty of Civil Engineering, Ho Chi Minh City Open University, Ho Chi Minh City, Vietnam

    Quoc-Hoa Pham & Phu-Cuong Nguyen

  2. Faculty of Mechanical Engineering, Le Quy Don Technical University, Hanoi, Vietnam

    Trung Thanh Tran

  3. Division of Computational Mathematics and Engineering, Institute for Computational Science, Ton Duc Thang University, Ho Chi Minh City, Vietnam

    Trung Nguyen-Thoi

  4. Faculty of Civil Engineering, Ton Duc Thang University, Ho Chi Minh City, Vietnam

    Trung Nguyen-Thoi

Authors
  1. Quoc-Hoa Pham
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Phu-Cuong Nguyen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Trung Thanh Tran
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Trung Nguyen-Thoi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Trung Nguyen-Thoi.

Ethics declarations

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A

Lagrange’s polynomial function:

$$N_{1} = \frac{1}{4}\left( {1 - \chi } \right)\left( {1 - \zeta } \right);$$
$$N_{2} = \frac{1}{4}\left( {1 + \chi } \right)\left( {1 - \zeta } \right);$$
$$N_{3} = \frac{1}{4}\left( {1 + \chi } \right)\left( {1 + \zeta } \right);$$

\(N_{4} = \frac{1}{4}\left( {1 - \chi } \right)\left( {1 + \zeta } \right)\).

Appendix B

Hermite’s polynomial function:

$$H_{1} = \frac{1}{8}\left( {1 - \chi } \right)\left( {1 - \zeta } \right)\left( {2 - \chi - \zeta - \chi^{2} - \zeta^{2} } \right)$$
$$H_{2} = \frac{1}{8}\left( {1 - \chi } \right)\left( {1 - \zeta } \right)\left( {1 - \chi^{2} } \right)$$
$$H_{3} = \frac{1}{8}\left( {1 - \chi } \right)\left( {1 - \zeta } \right)\left( {1 - \zeta^{2} } \right)$$
$$H_{4} = \frac{1}{8}\left( {1 + \chi } \right)\left( {1 - \zeta } \right)\left( {2 + \chi - \zeta - \chi^{2} - \zeta^{2} } \right)$$
$$H_{5} = \frac{1}{8}\left( {1 + \chi } \right)\left( {1 - \zeta } \right)\left( {1 - \chi^{2} } \right)$$
$$H_{6} = \frac{1}{8}\left( {1 + \chi } \right)\left( {1 - \zeta } \right)\left( {1 - \zeta^{2} } \right)$$
$$H_{7} = \frac{1}{8}\left( {1 + \chi } \right)\left( {1 + \zeta } \right)\left( {2 + \chi + \zeta - \chi^{2} - \zeta^{2} } \right)$$
$$H_{8} = \frac{1}{8}\left( {1 + \chi } \right)\left( {1 + \zeta } \right)\left( {1 - \chi^{2} } \right)$$
$$H_{9} = \frac{1}{8}\left( {1 + \chi } \right)\left( {1 + \zeta } \right)\left( {1 - \zeta^{2} } \right)$$
$$H_{10} = \frac{1}{8}\left( {1 - \chi } \right)\left( {1 + \zeta } \right)\left( {2 - \chi + \zeta - \chi^{2} - \zeta^{2} } \right)$$
$$H_{11} = \frac{1}{8}\left( {1 - \chi } \right)\left( {1 + \zeta } \right)\left( {1 - \chi^{2} } \right)$$
$$H_{12} = \frac{1}{8}\left( {1 - \chi } \right)\left( {1 + \zeta } \right)\left( {1 - \zeta^{2} } \right)$$

with \(\chi ,\zeta\) are natural coordinates.

Appendix C

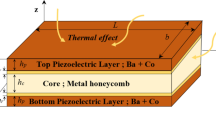
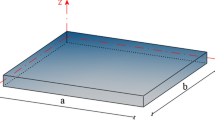
Geometrical parameters of sandwich nanoplates:

figure a

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pham, QH., Nguyen, PC., Tran, T.T. et al. Free vibration analysis of nanoplates with auxetic honeycomb core using a new third-order finite element method and nonlocal elasticity theory. Engineering with Computers 39, 233–251 (2023). https://doi.org/10.1007/s00366-021-01531-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-021-01531-3

Keywords

Search

Navigation