Skip to main content
SpringerLink
Log in

Smart laminates with an auxetic ply rested on visco-Pasternak medium: Active control of the system’s oscillation

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

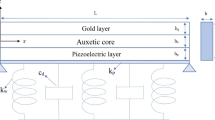
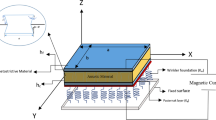
The time-dependent viscoelastic deflection characteristics of laminated composite structures consisted of an auxetic core respectively surrounded by piezoelectric and gold layers in bottom and top are studied in this paper for the first time. The material properties of the auxetic ply are achieved using a micromechanical scheme. The kinematic motion equation of the thin-walled plate, rested on a three-parameter viscoelastic medium, are then derived by inserting the displacement field of the Kirchhoff–Love plate theorem into the dynamic form of the principle of virtual work. The final governing equation of the dynamic problem is obtained by adding the constitutive equations of the laminate in the plate’s motion equation. The main objective of this project is to investigate the significant role of piezoelectric and auxetic layers’ thicknesses in the determination of the viscoelastic deflection-time curve of the system. Although the proportional active control system can manipulate the system’s fluctuation, it is reported that the damping coefficient of the visco-Pasternak substrate can act as an efficient passive damper.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Baughman RH (2003) Auxetic materials: avoiding the shrink. Nature 425(6959):667. https://doi.org/10.1038/425667a

    Article  Google Scholar 

  2. Wang Z, Zulifqar A, Hu H (2016) Auxetic composites in aerospace engineering. In: Rana S, Fangueiro R (eds) Advanced composite materials for aerospace engineering. Woodhead Publishing, pp 213–240. https://doi.org/10.1016/B978-0-08-100037-3.00007-9

  3. Yang W, Li Z-M, Shi W, Xie B-H, Yang M-B (2004) Review on auxetic materials. J Mater Sci 39(10):3269–3279. https://doi.org/10.1023/B:JMSC.0000026928.93231.e0

    Article  Google Scholar 

  4. Assidi M, Ganghoffer J-F (2012) Composites with auxetic inclusions showing both an auxetic behavior and enhancement of their mechanical properties. Compos Struct 94(8):2373–2382. https://doi.org/10.1016/j.compstruct.2012.02.026

    Article  Google Scholar 

  5. Dirrenberger J, Forest S, Jeulin D (2013) Effective elastic properties of auxetic microstructures: anisotropy and structural applications. Int J Mech Mater Des 9(1):21–33. https://doi.org/10.1007/s10999-012-9192-8

    Article  Google Scholar 

  6. Ge Z, Hu H, Liu Y (2013) A finite element analysis of a 3D auxetic textile structure for composite reinforcement. Smart Mater Struct 22(8):084005. https://doi.org/10.1088/0964-1726/22/8/084005

    Article  Google Scholar 

  7. Grima JN, Cauchi R, Gatt R, Attard D (2013) Honeycomb composites with auxetic out-of-plane characteristics. Compos Struct 106:150–159. https://doi.org/10.1016/j.compstruct.2013.06.009

    Article  Google Scholar 

  8. Kochmann DM, Venturini GN (2013) Homogenized mechanical properties of auxetic composite materials in finite-strain elasticity. Smart Mater Struct 22(8):084004. https://doi.org/10.1088/0964-1726/22/8/084004

    Article  Google Scholar 

  9. Hou Y, Neville R, Scarpa F, Remillat C, Gu B, Ruzzene M (2014) Graded conventional-auxetic Kirigami sandwich structures: Flatwise compression and edgewise loading. Compos B Eng 59:33–42. https://doi.org/10.1016/j.compositesb.2013.10.084

    Article  Google Scholar 

  10. Imbalzano G, Tran P, Ngo TD, Lee PVS (2016) A numerical study of auxetic composite panels under blast loadings. Compos Struct 135:339–352. https://doi.org/10.1016/j.compstruct.2015.09.038

    Article  Google Scholar 

  11. Jiang L, Gu B, Hu H (2016) Auxetic composite made with multilayer orthogonal structural reinforcement. Compos Struct 135:23–29. https://doi.org/10.1016/j.compstruct.2015.08.110

    Article  Google Scholar 

  12. Fu M-H, Chen Y, Hu L-L (2017) A novel auxetic honeycomb with enhanced in-plane stiffness and buckling strength. Compos Struct 160:574–585. https://doi.org/10.1016/j.compstruct.2016.10.090

    Article  Google Scholar 

  13. Jiang L, Hu H (2017) Low-velocity impact response of multilayer orthogonal structural composite with auxetic effect. Compos Struct 169:62–68. https://doi.org/10.1016/j.compstruct.2016.10.018

    Article  Google Scholar 

  14. Duc ND, Cong PH (2018) Nonlinear dynamic response and vibration of sandwich composite plates with negative Poisson’s ratio in auxetic honeycombs. J Sandw Struct Mater 20(6):692–717. https://doi.org/10.1177/1099636216674729

    Article  Google Scholar 

  15. Behravan Rad A (2018) Static analysis of non-uniform 2D functionally graded auxetic-porous circular plates interacting with the gradient elastic foundations involving friction force. Aerosp Sci Technol 76:315–339. https://doi.org/10.1016/j.ast.2018.01.036

    Article  Google Scholar 

  16. Zhu X, Zhang J, Zhang W, Chen J (2019) Vibration frequencies and energies of an auxetic honeycomb sandwich plate. Mech Adv Mater Struct 26(23):1951–1957. https://doi.org/10.1080/15376494.2018.1455933

    Article  Google Scholar 

  17. Hajmohammad MH, Nouri AH, Sharif Zarei M, Kolahchi R (2019) A new numerical approach and visco-refined zigzag theory for blast analysis of auxetic honeycomb plates integrated by multiphase nanocomposite facesheets in hygrothermal environment. Eng Comput 35(4):1141–1157. https://doi.org/10.1007/s00366-018-0655-x

    Article  Google Scholar 

  18. Ebrahimi F, Dabbagh A (2019) Vibration analysis of graphene oxide powder-/carbon fiber-reinforced multi-scale porous nanocomposite beams: a finite-element study. Eur Phys J Plus 134(5):225. https://doi.org/10.1140/epjp/i2019-12594-1

    Article  Google Scholar 

  19. Ebrahimi F, Dabbagh A, Civalek Ö (2019) Vibration analysis of magnetically affected graphene oxide-reinforced nanocomposite beams. J Vib Control 25(23–24):2837–2849. https://doi.org/10.1177/1077546319861002

    Article  MathSciNet  Google Scholar 

  20. Ebrahimi F, Nouraei M, Dabbagh A, Rabczuk T (2019) Thermal buckling analysis of embedded graphene-oxide powder-reinforced nanocomposite plates. Adv Nano Res 7(5):293–310. https://doi.org/10.12989/ANR.2019.7.5.293

    Article  Google Scholar 

  21. Ebrahimi F, Dabbagh A, Rastgoo A, Rabczuk T (2020) Agglomeration effects on static stability analysis of multi-scale hybrid nanocomposite plates. Comput Mater Continua 63(1):41–64. https://doi.org/10.32604/cmc.2020.07947

    Article  Google Scholar 

  22. Ebrahimi F, Dabbagh A (2020) Mechanics of nanocomposites: homogenization and Analysis, 1st edn. CRC Press, Boca Raton. https://doi.org/10.1201/9780429316791

  23. Ebrahimi F, Dabbagh A (2020) A brief review on the influences of nanotubes’ entanglement and waviness on the mechanical behaviors of CNTR polymer nanocomposites. J Comput Appl Mech 51(1):247–252. https://doi.org/10.22059/jcamech.2020.304476.517

    Article  Google Scholar 

  24. Dabbagh A, Rastgoo A, Ebrahimi F (2021) Static stability analysis of agglomerated multi-scale hybrid nanocomposites via a refined theory. Eng Comput 37(3):2225–2244. https://doi.org/10.1007/s00366-020-00939-7

    Article  Google Scholar 

  25. Amani MA, Ebrahimi F, Dabbagh A, Rastgoo A, Nasiri MM (2021) A machine learning-based model for the estimation of the temperature-dependent moduli of graphene oxide reinforced nanocomposites and its application in a thermally affected buckling analysis. Eng Comput 37(3):2245–2255. https://doi.org/10.1007/s00366-020-00945-9

    Article  Google Scholar 

  26. Ebrahimi F, Dabbagh A, Rastgoo A (2021) Free vibration analysis of multi-scale hybrid nanocomposite plates with agglomerated nanoparticles. Mech Based Des Struct Mach 49(4):487–510. https://doi.org/10.1080/15397734.2019.1692665

    Article  Google Scholar 

  27. Ranjbar M, Boldrin L, Scarpa F, Neild S, Patsias S (2016) Vibroacoustic optimization of anti-tetrachiral and auxetic hexagonal sandwich panels with gradient geometry. Smart Mater Struct 25(5):054012. https://doi.org/10.1088/0964-1726/25/5/054012

    Article  Google Scholar 

  28. Billon K, Zampetakis I, Scarpa F, Ouisse M, Sadoulet-Reboul E, Collet M, Perriman A, Hetherington A (2017) Mechanics and band gaps in hierarchical auxetic rectangular perforated composite metamaterials. Compos Struct 160:1042–1050. https://doi.org/10.1016/j.compstruct.2016.10.121

    Article  Google Scholar 

  29. Mazloomi MS, Ranjbar M, Boldrin L, Scarpa F, Patsias S, Ozada N (2018) Vibroacoustics of 2D gradient auxetic hexagonal honeycomb sandwich panels. Compos Struct 187:593–603. https://doi.org/10.1016/j.compstruct.2017.10.077

    Article  Google Scholar 

  30. Nourafkan M, Mohammadi E, Manavizadeh N (2019) Influence of the ZnO nanostructures shape on piezoelectric energy harvesters performance. IEEE Trans Electron Devices 66(11):4989–4996. https://doi.org/10.1109/TED.2019.2942777

    Article  Google Scholar 

  31. Gualtieri JG, Kosinski JA, Ballato A (1994) Piezoelectric materials for acoustic wave applications. IEEE Trans Ultrason Ferroelectr Freq Control 41(1):53–59. https://doi.org/10.1109/58.265820

    Article  Google Scholar 

  32. Quan TQ, Anh VM, Mahesh V, Duc ND (2020) Vibration and nonlinear dynamic response of imperfect sandwich piezoelectric auxetic plate. Mech Adv Mater Struct. https://doi.org/10.1080/15376494.2020.1752864

    Article  Google Scholar 

  33. Vu-Bac N, Lahmer T, Zhuang X, Nguyen-Thoi T, Rabczuk T (2016) A software framework for probabilistic sensitivity analysis for computationally expensive models. Adv Eng Softw 100:19–31. https://doi.org/10.1016/j.advengsoft.2016.06.005

    Article  Google Scholar 

  34. Reddy JN (2003) Mechanics of laminated composite plates and shells: theory and analysis, 2nd edn. CRC Press, Boca Raton

    Book  Google Scholar 

  35. Lai WM, Rubin D, Krempl E (2009) Introduction to continuum mechanics, 4th edn. Butterworth-Heinemann, Oxford

    MATH  Google Scholar 

  36. Ebrahimi F, Dabbagh A (2019) Vibration analysis of multi-scale hybrid nanocomposite plates based on a Halpin-Tsai homogenization model. Compos B Eng 173:106955. https://doi.org/10.1016/j.compositesb.2019.106955

    Article  Google Scholar 

  37. Li J, Xue Y, Li F, Narita Y (2019) Active vibration control of functionally graded piezoelectric material plate. Compos Struct 207:509–518. https://doi.org/10.1016/j.compstruct.2018.09.053

    Article  Google Scholar 

  38. Ebrahimi F, Dabbagh A (2018) On wave dispersion characteristics of double-layered graphene sheets in thermal environments. J Electromagn Waves Appl 32(15):1869–1888. https://doi.org/10.1080/09205071.2017.1417918

    Article  Google Scholar 

  39. Yarali E, Farajzadeh MA, Noroozi R, Dabbagh A, Khoshgoftar MJ, Mirzaali MJ (2020) Magnetorheological elastomer composites: modeling and dynamic finite element analysis. Compos Struct 254:112881. https://doi.org/10.1016/j.compstruct.2020.112881

    Article  Google Scholar 

  40. Ebrahimi F, Dabbagh A, Rabczuk T (2021) On wave dispersion characteristics of magnetostrictive sandwich nanoplates in thermal environments. Eur J Mech A Solids 85:104130. https://doi.org/10.1016/j.euromechsol.2020.104130

    Article  MathSciNet  MATH  Google Scholar 

  41. Ebrahimi F, Nopour R, Dabbagh A (2021) Effect of viscoelastic properties of polymer and wavy shape of the CNTs on the vibrational behaviors of CNT/glass fiber/polymer plates. Eng Comput. https://doi.org/10.1007/s00366-021-01387-7

    Article  Google Scholar 

  42. Anitescu C, Atroshchenko E, Alajlan N, Rabczuk T (2019) Artificial neural network methods for the solution of second order boundary value problems. Comput Mater Continua 59(1):345–359. https://doi.org/10.32604/cmc.2019.06641

    Article  Google Scholar 

  43. Guo H, Zhuang X, Rabczuk T (2019) A deep collocation method for the bending analysis of Kirchhoff Plate. Comput Mater Continua 59(2):433–456. https://doi.org/10.32604/cmc.2019.06660

    Article  Google Scholar 

  44. Samaniego E, Anitescu C, Goswami S, Nguyen-Thanh VM, Guo H, Hamdia K, Zhuang X, Rabczuk T (2020) An energy approach to the solution of partial differential equations in computational mechanics via machine learning: Concepts, implementation and applications. Comput Methods Appl Mech Eng 362:112790. https://doi.org/10.1016/j.cma.2019.112790

    Article  MathSciNet  MATH  Google Scholar 

  45. Nguyen-Thanh VM, Anitescu C, Alajlan N, Rabczuk T, Zhuang X (2021) Parametric deep energy approach for elasticity accounting for strain gradient effects. Comput Methods Appl Mech Eng 386:114096. https://doi.org/10.1016/j.cma.2021.114096

    Article  MathSciNet  MATH  Google Scholar 

  46. Ebrahimi F, Dabbagh A (2017) On flexural wave propagation responses of smart FG magneto-electro-elastic nanoplates via nonlocal strain gradient theory. Compos Struct 162:281–293. https://doi.org/10.1016/j.compstruct.2016.11.058

    Article  Google Scholar 

  47. Song M, Kitipornchai S, Yang J (2017) Free and forced vibrations of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos Struct 159:579–588. https://doi.org/10.1016/j.compstruct.2016.09.070

    Article  Google Scholar 

  48. García-Macías E, Rodríguez-Tembleque L, Sáez A (2018) Bending and free vibration analysis of functionally graded graphene vs. carbon nanotube reinforced composite plates. Compos Struct 186:123–138. https://doi.org/10.1016/j.compstruct.2017.11.076

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Faculty of Engineering, Imam Khomeini International University, Qazvin, Iran

    Farzad Ebrahimi & Reza Nopour

  2. School of Mechanical Engineering, College of Engineering, University of Tehran, Tehran, Iran

    Ali Dabbagh

Authors
  1. Farzad Ebrahimi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Reza Nopour
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ali Dabbagh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Farzad Ebrahimi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ebrahimi, F., Nopour, R. & Dabbagh, A. Smart laminates with an auxetic ply rested on visco-Pasternak medium: Active control of the system’s oscillation. Engineering with Computers 39, 221–231 (2023). https://doi.org/10.1007/s00366-021-01533-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-021-01533-1

Keywords

Search

Navigation