Nonlinear vibration analysis of bidirectional porous beams

Abstract

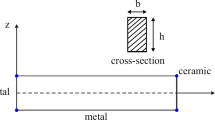
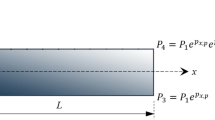
This paper presents nonlinear vibration behavior of shear deformable bidirectional porous beams with non-uniform porosity distribution. A new porosity distributions are proposed to maximize natural frequencies of the porous beam. It is assumed that closed-cell voids are distributed along the thickness and length of the beam. Hamilton principle is used to derive nonlinear governing equations using Reddy beam theory considering von Karman geometrical nonlinearity. Generalized differential quadrature method, harmonic balance approach along with the Picard iterative approach are used to discretize and solve the nonlinear dynamic equations. The variation of nonlinear frequency versus the vibration amplitude is highlighted considering various influential factors such as geometrical parameters, porosity distributions, beam theories and boundary conditions. It is shown that the newly defined porosity distribution can increase the frequencies in comparison to the conventional porosity distribution. Comparing beams of the same weight shows that porosities near the center of the beam further increases frequencies in comparison to the other porosity distributions. Moreover, bidirectional porosity increases the frequencies in comparison to the unidirectional porosity. Frequencies of the bidirectional porous Reddy beam depend not only on the bending stiffness, as in the case of unidirectional porous beam, but also on the first derivative of the bending stiffness.

Appendix

Elements of the stiffness $\left({K}_{ij}\right)$ and mass $\left({M}_{ij}\right)$ matrices of the bidirectional porous beams are:

$$ K_{11} = A_{xx} \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial A_{xx} }}{\partial x}\frac{\partial }{\partial x} $$

$$ K_{12} = 0 $$

$$ K_{13} = A_{xx} \frac{\partial }{\partial x}\frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial A_{xx} }}{\partial x}\frac{1}{2}\left( {\frac{\partial }{\partial x}} \right)^{2} $$

$$ K_{21} = A_{xx} \frac{\partial w}{{\partial x}}\frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial A_{xx} }}{\partial x}\frac{\partial w}{{\partial x}}\frac{\partial }{\partial x} + A_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{\partial }{\partial x} $$

$$ \begin{aligned} K_{22} =\, & c_{1} \left( {c_{1} A_{xz} - c_{2} D_{xz} } \right)\frac{\partial }{\partial x} + c_{1} \left( {c_{1} \frac{{\partial A_{xz} }}{\partial x} - c_{2} \frac{{\partial D_{xz} }}{\partial x}} \right) \\ & - c_{2} \left( {c_{1} D_{xz} - c_{2} F_{xz} } \right)\frac{\partial }{\partial x} - c_{2} \left( {c_{1} \frac{{\partial D_{xz} }}{\partial x} - c_{2} \frac{{\partial F_{xz} }}{\partial x}} \right) \\ & + c_{3} \left( \begin{gathered} c_{1} \frac{{\partial^{2} F_{xx} }}{{\partial x^{2} }}\frac{\partial }{\partial x} + 2c_{1} \frac{{\partial F_{xx} }}{\partial x}\frac{{\partial^{2} }}{{\partial x^{2} }} + F_{xx} c_{1} \frac{{\partial^{3} }}{{\partial x^{3} }} \hfill \\ - c_{3} \frac{{\partial^{2} H_{xx} }}{{\partial x^{2} }}\frac{\partial }{\partial x} - 2c_{3} \frac{{\partial H_{xx} }}{\partial x}\frac{{\partial^{2} }}{{\partial x^{2} }} - c_{3} H_{xx} \frac{{\partial^{3} }}{{\partial x^{3} }} \hfill \\ \end{gathered} \right) \\ \end{aligned} $$

$$ \begin{aligned} K_{23} = & \left( {A_{xx} \frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{2}\frac{{\partial A_{xx} }}{\partial x}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \right)\frac{\partial }{\partial x} \\ & + \frac{1}{2}A_{xx} \left( {\frac{\partial w}{{\partial x}}} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }} + \left( {1 - c_{0} } \right)\left( \begin{gathered} \left( {c_{1} A_{xz} - c_{2} D_{xz} } \right)\frac{{\partial^{2} }}{{\partial x^{2} }} \hfill \\ + \left( {c_{1} \frac{{\partial A_{xz} }}{\partial x} - c_{2} \frac{{\partial D_{xz} }}{\partial x}} \right)\frac{\partial }{\partial x} \hfill \\ \end{gathered} \right) \\ & - c_{2} \left( {\left( {c_{1} D_{xz} - c_{2} F_{xz} } \right)\frac{{\partial^{2} }}{{\partial x^{2} }} + \left( {c_{1} \frac{{\partial D_{xz} }}{\partial x} - c_{2} \frac{{\partial F_{xz} }}{\partial x}} \right)\frac{\partial }{\partial x}} \right) \\ & - c_{3} \left( \begin{gathered} c_{0} \frac{{\partial^{2} F_{xx} }}{{\partial x^{2} }}\frac{{\partial^{2} }}{{\partial x^{2} }} + 2c_{0} \frac{{\partial F_{xx} }}{\partial x}\frac{{\partial^{3} }}{{\partial x^{3} }} + F_{xx} c_{0} \frac{{\partial^{4} }}{{\partial x^{4} }} \hfill \\ + c_{3} \frac{{\partial^{2} H_{xx} }}{{\partial x^{2} }}\frac{{\partial^{2} }}{{\partial x^{2} }} + 2c_{3} \frac{{\partial H_{xx} }}{\partial x}\frac{{\partial^{3} }}{{\partial x^{3} }} + c_{3} H_{xx} \frac{{\partial^{4} }}{{\partial x^{4} }} \hfill \\ \end{gathered} \right) \\ \end{aligned} $$

$$ K_{31} = 0 $$

$$\begin{aligned}{K_{32}} = &c_1^2\left( {{D_{xx}}\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{\partial {D_{xx}}}}{{\partial x}}\frac{\partial }{{\partial x}}} \right)\\& - 2{c_1}{c_3}\left( {{F_{xx}}\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{\partial {F_{xx}}}}{{\partial x}}\frac{\partial }{{\partial x}}} \right) \\& +c_3^2\left( {{H_{xx}}\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{\partial {H_{xx}}}}{{\partial x}}\frac{\partial }{{\partial x}}} \right) \\&- {c_1}\left( {{c_1}{A_{xz}} - {c_2}{D_{xz}}} \right)\\& + {c_2}\left( {{c_1}{D_{xz}} - {c_2}{F_{xz}}} \right)\end{aligned}$$

$$ \begin{aligned} K_{33} = & - c_{1} c_{0} \left( {D_{xx} \frac{{\partial^{3} }}{{\partial x^{3} }} + \frac{{\partial D_{xx} }}{\partial x}\frac{{\partial^{2} }}{{\partial x^{2} }}} \right) \\ & - c_{1} c_{3} \left( {F_{xx} \frac{{\partial^{3} }}{{\partial x^{3} }} + \frac{{\partial F_{xx} }}{\partial x}\frac{{\partial^{2} }}{{\partial x^{2} }}} \right) \\ & + c_{3} c_{0} \left( {F_{xx} \frac{{\partial^{3} }}{{\partial x^{3} }} + \frac{{\partial F_{xx} }}{\partial x}\frac{{\partial^{2} }}{{\partial x^{2} }}} \right) \\ & + c_{3}^{2} \left( {H_{xx} \frac{{\partial^{3} }}{{\partial x^{3} }} + \frac{{\partial H_{xx} }}{\partial x}\frac{{\partial^{2} }}{{\partial x^{2} }}} \right) \\ & - \left( \begin{gathered} \left( {1 - c_{0} } \right)\left( {c_{1} A_{xz} - c_{2} D_{xz} } \right) \hfill \\ - c_{2} \left( {c_{1} D_{xz} - c_{2} F_{xz} } \right) \hfill \\ \end{gathered} \right)\frac{\partial }{\partial x} \\ \end{aligned} $$

$$ M_{11} = I_{0} ;\quad M_{12} = J_{1} ;\quad M_{13} = - K_{1} \frac{\partial }{\partial x} $$

$$ \begin{aligned} & {\text{M}}_{21} = - K_{1} \frac{\partial }{\partial x}{ };{\text{ M}}_{22} = - \left( {c_{1} K_{2} - c_{3} K_{4} } \right)\frac{\partial }{\partial x}{ };\\&{\text{ M}}_{23} = \left( {c_{0} K_{2} + c_{3} K_{4} } \right)\frac{{\partial^{2} }}{{\partial x^{2} }} + I_{0} \end{aligned} $$

$$ {\text{M}}_{31} = J_{1} { };{\text{ M}}_{32} = c_{1} J_{2} - c_{3} J_{4} { };{\text{ M}}_{33} = - \left( {c_{0} J_{2} + c_{3} J_{4} } \right)\frac{\partial }{\partial x} $$

As an example, a discretized form of the first equation in the equation set 22 based on the GDQ method is given here:

$$ \begin{gathered} \delta u:\mathop \sum \limits_{j = 1}^{{N_{x} }} \left[ \begin{gathered} C_{{x_{ij} }}^{\left( 2 \right)} A_{xx} u\left( {x_{j} } \right) + C_{{x_{ij} }}^{\left( 1 \right)} \frac{{\partial A_{xx} }}{\partial x}u\left( {x_{j} } \right) \hfill \\ + C_{{x_{ij} }}^{\left( 3 \right)} A_{xx} w\left( {x_{j} } \right) + C_{{x_{ij} }}^{\left( 1 \right)} C_{{x_{ij} }}^{\left( 1 \right)} \frac{{\partial A_{xx} }}{\partial x}\frac{1}{2}\left( {w\left( {x_{j} } \right)} \right)^{2} \hfill \\ \end{gathered} \right] \hfill \\ \quad = \mathop \sum \limits_{i = 1}^{{N_{x} }} \left[ {I_{0} u\left( {x_{j} } \right) + J_{1} \phi \left( {x_{j} } \right) - K_{1} C_{{x_{ij} }}^{\left( 1 \right)} w\left( {x_{j} } \right)} \right], \hfill \\ i = 1,2, \ldots , N_{x} \hfill \\ \end{gathered} $$

In addition, the discretized boundary conditions can be obtained as follows. For instance, for the clamped boundaries at $x=0$ and $x=L$, following conditions on both ends of the beam should be satisfied.

$$ u = \phi = w = \mathop \sum \limits_{j = 1}^{{N_{x} }} C_{{x_{ij} }}^{\left( 1 \right)} w\left( {x_{j} } \right) = 0 $$

Similarly, the discretized boundary conditions for the case of simply supported edges can be obtained.