Skip to main content
Springer Nature Link
Log in

Optimized differential evolution algorithm for solving DEM material calibration problem

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

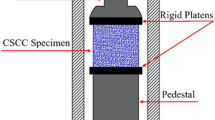
Abstract

The discrete element method (DEM) micro parameter calibration has been a longstanding problem since the DEM was created. To date, the low-precision and time-consuming calibration procedures still pose difficulties for DEM applications. This study proposed an optimized differential evolution calibration method (OpDEC) to calibrate cohesive granular DEM material to the target macro mechanical properties. Macro parameter Young’s modulus, Poisson’s ratio, uniaxial compressive strength, and direct tensile strength can be calibrated to less than 5% weighted relative error within 5 h or less than 1% weighted relative error within 12.5 h. For this purpose, 180 calibrations were carried out to optimize the mutation strategy and control parameters of the differential evolution algorithm. A calibration evolutionary health monitoring scheme was devised to detect the possible ill calibrations in early time. The algorithm robustness was verified by 50 calibrations of 5 types of rock. Moreover, a laboratory-tested stress–strain curve of Äspö diorite was compared with 10 calibrated DEM models that showed a good agreement in terms of axial behaviour. The OpDEC has a great potential to serve as a fast and easy-to-implement method to calibrate the cohesive granular DEM material.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Code availability

The OpDEC (optimized differential evolution calibration algorithm) is an open-source project (https://doi.org/10.14264/ca1267d). It may be re-used in any research outputs where reliance is made upon it, including conference papers and published research papers. This project and data are also licensed with Permitted Re-Use with Acknowledgement standard licensing agreement of UQ eSpace.

Abbreviations

D :

The dimension of vectors

g :

The index of population generation

N P :

The number of vectors in a population

P x,g :

The population of generation g

x i,g :

Vectors within populations Px,g with index i

x j,i,g :

Parameters within vectors with index j

b j,i, low :

Lower bounds of parameters

b j,i, up :

Upper bounds of parameters

v i,g :

Intermediary/mutant vector

F :

Mutation scale factor

x r,g :

Randomly chosen vector

x best :

Vector with the best result of the target function

P u,g :

Trial population

u i,g :

Vectors within trial population Pu,g with index i

Cr:

Crossover probability

j rand :

A randomly chosen number

P ma,sim :

PFC Simulated macro parameters

P ma,tar :

Target macro parameters

REsum :

Sum of relative errors of Pma_sim and Pma_tar

w i :

Weighting factors for each macro parameter

p cen :

Centre values of micro parameters

p bia :

Centre biases of micro parameters

p mi_low :

Lower bounds of micro parameters

p mi_up :

Upper bounds of micro parameters

v :

The velocity of loading walls

lr:

Loading rate

H :

Specimen Height

L :

Contact distance for particles/wall

c mi :

Cohesion-micro

σ tmi :

Tensile strength-micro

τ mi :

Shear strength-micro

E mi :

Effective modulus-micro

k n :

Normal stiffness-micro

k s :

Shear stiffness-micro

k mi :

Normal-to-shear stiffness ratio-micro

µ mi :

Friction coefficient-micro

ϕ mi :

Friction angle-micro

σ 1 :

Major principal stress

σ 3 :

Minor principal stress

σ cma :

Uniaxial compressive strength-macro

σ tma :

Direct tensile strength-macro

E ma :

Young’s modulus-macro

ν ma :

Poisson’s ratio-macro

ϕ ma :

Friction angle-macro

c ma :

Cohesion-macro

References

  1. Cundall PA, Strack ODL (1979) A discrete numerical model for granular assemblies. Geotechnique 29(1):47–65

    Google Scholar 

  2. Karkala S, Davis N, Wassgren C, Shi Y, Liu X, Riemann C et al (2019) Calibration of discrete-element-method parameters for cohesive materials using dynamic-yield-strength and shear-cell experiments. Processes 7(5):278

    Google Scholar 

  3. Wang J, Apel DB, Pu Y, Hall R, Wei C, Sepehri M (2020) Numerical modeling for rockbursts: a state-of-the-art review. J Rock Mech Geotech Eng 83(9):324

    Google Scholar 

  4. Potyondy DO, Cundall PA (2004) A bonded-particle model for rock. Int J Rock Mech Min Sci 41(8):1329–1364

    Google Scholar 

  5. Khanal M, Elmouttie M, Poulsen B, Olsson A, Adhikary D (2017) Effect of loading rate on sand pile failure: 2D DEM simulation. Geotech Geol Eng 35(2):889–896

    Google Scholar 

  6. Yin D, Chen S, Liu X, Ma H (2018) Effect of joint angle in coal on failure mechanical behaviour of roof rock-coal combined body. Q J Eng Geol Hydrogeol 51(2):202–209

    Google Scholar 

  7. Kulatilake PHSW, Malama B, Wang J (2001) Physical and particle flow modeling of jointed rock block behavior under uniaxial loading. Int J Rock Mech Min Sci 38(5):641–657

    Google Scholar 

  8. Boutt DF (2002) Simulation of sedimentary rock deformation: lab-scale model calibration and parameterization. Geophys Res Lett 29(4):603

    Google Scholar 

  9. André D, Girardot J, Hubert C (2019) A novel DEM approach for modeling brittle elastic media based on distinct lattice spring model. Comput Methods Appl Mech Eng 350:100–122

    MathSciNet  MATH  Google Scholar 

  10. Celigueta MA, Latorre S, Arrufat F, Oñate E (2017) Accurate modelling of the elastic behavior of a continuum with the discrete element method. Comput Mech 60(6):997–1010

    MathSciNet  MATH  Google Scholar 

  11. Shao Q, Matthäi SK, Gross L (2019) Efficient modelling of solute transport in heterogeneous media with discrete event simulation. J Comput Phys 384:134–150

    MathSciNet  MATH  Google Scholar 

  12. Cheng H, Shuku T, Thoeni K, Tempone P, Luding S, Magnanimo V (2019) An iterative Bayesian filtering framework for fast and automated calibration of DEM models. Comput Methods Appl Mech Eng 350:268–294

    MathSciNet  MATH  Google Scholar 

  13. Yoon J (2007) Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation. Int J Rock Mech Min Sci 44(6):871–889

    Google Scholar 

  14. Coetzee CJ (2017) Review: calibration of the discrete element method. Powder Technol 310:104–142

    Google Scholar 

  15. Wu S, Xu X (2016) A study of three intrinsic problems of the classic discrete element method using flat-joint model. Rock Mech Rock Eng 49(5):1813–1830

    Google Scholar 

  16. Vallejos JA, Salinas JM, Delonca A, Mas ID (2017) Calibration and verification of two bonded-particle models for simulation of intact rock behavior. Int J Geomech 17(4):6016030

    Google Scholar 

  17. Chen P-y (2017) Effects of microparameters on macroparameters of flat-jointed bonded-particle materials and suggestions on trial-and-error method. Geotech Geol Eng 35(2):663–677

    Google Scholar 

  18. Castro-Filgueira U, Alejano LR, Arzúa J, Ivars DM (2017) Sensitivity analysis of the micro-parameters used in a PFC analysis towards the mechanical properties of rocks. Procedia Eng 191:488–495

    Google Scholar 

  19. Potyondy DO (2019) Material-Modeling Support in PFC [fistPkg6.5]: Technical Memorandum ICG7766-L. https://www.itascacg.com/material-modeling-support. Accessed 22 May 2019.

  20. Tsang M, Karlovsek J (2020) Automating the calibration of flat-jointed bonded particle model microproperties for a porous rock. Unpublished manuscript

  21. Zou Q, Lin B (2017) Modeling the relationship between macro- and meso-parameters of coal using a combined optimization method. Environ Earth Sci 76(14):479

    Google Scholar 

  22. Wang Y, Tonon F (2010) Calibration of a discrete element model for intact rock up to its peak strength. Int J Numer Anal Methods Geomech 34(5):447–469

    MATH  Google Scholar 

  23. Wang M, Cao P (2017) Calibrating the micromechanical parameters of the PFC2D(3D) models using the improved simulated annealing algorithm. Math Probl Eng 2017(1):1–11

    MathSciNet  Google Scholar 

  24. de Simone M, Souza LMS, Roehl D (2019) Estimating DEM microparameters for uniaxial compression simulation with genetic programming. Int J Rock Mech Min Sci 118:33–41

    Google Scholar 

  25. Do HQ, Aragón AM, Schott DL (2018) A calibration framework for discrete element model parameters using genetic algorithms. Adv Powder Technol 29(6):1393–1403

    Google Scholar 

  26. Wang M, Lu Z, Wan W, Zhao Y (2021) A calibration framework for the microparameters of the DEM model using the improved PSO algorithm. Adv Powder Technol 32(2):358–369

    Google Scholar 

  27. Benvenuti L, Kloss C, Pirker S (2016) Identification of DEM simulation parameters by artificial neural networks and bulk experiments. Powder Technol 291:456–465

    Google Scholar 

  28. Karaboğa D, Ökdem S (2004) A simple and global optimization algorithm for engineering problems: differential evolution algorithm. Turk J Electr Eng Comput Sci 12(1):53–60

    Google Scholar 

  29. Ji S, Karlovšek J (2020) DE_Calibration_DEM_Material. Data Collection: The University of Queensland. https://doi.org/10.14264/932400a

  30. Brest J, Greiner S, Boskovic B, Mernik M, Zumer V (2006) Self-adapting control parameters in differential evolution: a comparative study on numerical benchmark problems. IEEE Trans Evol Comput 10(6):646–657

    Google Scholar 

  31. Elsayed SM, Sarker RA, Essam DL (2011) Differential evolution with multiple strategies for solving CEC2011 real-world numerical optimization problems. In: 2011 IEEE congress on evolutionary computation. IEEE, Piscataway, pp 1041–1048

  32. PyGMO 1.1.7dev documentation. https://esa.github.io/pygmo/index.html. Accessed 30 Oct 2020

  33. Rutkowski L, Korytkowski M, Scherer R, Tadeusiewicz R, Zadeh LA, Zurada JM et al (eds) (2014) Investigation of mutation strategies in differential evolution for solving global optimization problems: artificial intelligence and soft computing. Springer International Publishing, Berlin

    Google Scholar 

  34. Price KV, Storn RM, Lampinen JA (2005) Differential evolution: a practical approach to global optimization. Springer, Berlin

    MATH  Google Scholar 

  35. Opara K, Arabas J (2018) Comparison of mutation strategies in differential evolution—a probabilistic perspective. Swarm Evol Comput 39:53–69

    Google Scholar 

  36. Storn R (1996) On the usage of differential evolution for function optimization. In: Smith MHE (eds) 1996 Biennial conference of the North American fuzzy Information processing society: NAFIPS. IEEE, pp 519–523

  37. Qin AK, Huang VL, Suganthan PN (2009) Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Trans Evol Comput 13(2):398–417

    Google Scholar 

  38. He J, Yao X (2004) A study of drift analysis for estimating computation time of evolutionary algorithms. Nat Comput 3(1):21–35

    MathSciNet  MATH  Google Scholar 

  39. Piotrowski AP (2017) Review of differential evolution population size. Swarm Evol Comput 32:1–24

    Google Scholar 

  40. Storn R, Price K (1997) Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J Glob Optim 11(4):341–359

    MathSciNet  MATH  Google Scholar 

  41. Neri F, Tirronen V (2008) On memetic differential evolution frameworks: a study of advantages and limitations in hybridization. In: Staff I (ed) 2008 IEEE congress on evolutionary computation. IEEE, Hong Kong, pp 2135–2142

    Google Scholar 

  42. Ronkkonen J, Kukkonen S, Price KV (2005) Real-parameter optimization with differential evolution. In: 2005 IEEE congress on evolutionary computation. IEEE, Edinburgh, pp 506–513

  43. Brest J, Boskovic B, Zamuda A, Fister I, Maucec MS (2012) Self-adaptive differential evolution algorithm with a small and varying population size. In: 2012 IEEE congress on evolutionary computation. IEEE, Brisbane, pp 1–8

  44. Das R, Prasad DK (2015) Prediction of porosity and thermal diffusivity in a porous fin using differential evolution algorithm. Swarm Evol Comput 23:27–39

    Google Scholar 

  45. Satapathy SC, Naik A (2014) Modified teaching–learning-based optimization algorithm for global numerical optimization—a comparative study. Swarm Evol Comput 16:28–37

    Google Scholar 

  46. Wu G, Mallipeddi R, Suganthan PN, Wang R, Chen H (2016) Differential evolution with multi-population based ensemble of mutation strategies. Inf Sci 329:329–345

    Google Scholar 

  47. Neri F, Tirronen V (2010) Recent advances in differential evolution: a survey and experimental analysis. Artif Intell Rev 33(1):61–106

    Google Scholar 

  48. Das S, Suganthan PN (2011) Differential evolution: a survey of the state-of-the-art. IEEE Trans Evol Comput 15(1):4–31

    Google Scholar 

  49. Neri F, Tirronen V (2009) Scale factor local search in differential evolution. Memet Comput 1(2):153–171

    Google Scholar 

  50. Weber M, Neri F, Tirronen V (2011) A study on scale factor in distributed differential evolution. Inf Sci 181(12):2488–2511

    Google Scholar 

  51. Davidor Y, Schwefel H-P, Männer R, Potter MA, Jong KA de (eds.) (1994) A cooperative coevolutionary approach to function optimization: parallel problem solving from nature—PPSN III. Springer, Berlin

  52. Angeline PJ, Reynolds RG, McDonnell JR, Eberhart R, Salomon R (eds.) (1997) Raising theoretical questions about the utility of genetic algorithms: evolutionary programming VI. Springer, Berlin

  53. Chen SJ, Yin DW, Jiang N, Wang F, Guo WJ (2019) Simulation study on effects of loading rate on uniaxial compression failure of composite rock-coal layer. Geomech Eng 17(4):333–342

    Google Scholar 

  54. Itasca (2018) PFC (particle flow code in 2 and 3 dimensions), version 5.0 [User’s manual]

  55. Zhao Z, Sun W, Chen S, Yin D, Liu H, Chen B (2021) Determination of critical criterion of tensile-shear failure in Brazilian disc based on theoretical analysis and meso-macro numerical simulation. Comput Geotech 134(11):104096

    Google Scholar 

  56. Fakhimi A, Villegas T (2007) Application of dimensional analysis in calibration of a discrete element model for rock deformation and fracture. Rock Mech Rock Eng 40(2):193–211

    Google Scholar 

  57. Potyondy DO (2012) A flat-jointed bonded-particle material for hard rock. In: Bobet A (ed) 46th US rock mechanics. American Rock Mechanics Association, Alexandria

  58. Benjamini Y (1988) Opening the box of a boxplot. Am Stat 42(4):257–262

    Google Scholar 

  59. Zhao S, Zhao J, Liang W (2021) A thread-block-wise computational framework for large-scale hierarchical continuum-discrete modeling of granular media. Int J Numer Methods Eng 122(2):579–608

    MathSciNet  Google Scholar 

  60. Zhao S, Zhao J (2021) SudoDEM: unleashing the predictive power of the discrete element method on simulation for non-spherical granular particles. Comput Phys Commun 259(1):107670

    MathSciNet  MATH  Google Scholar 

  61. Nicksiar M, Martin CD (2012) Evaluation of methods for determining crack initiation in compression tests on low-porosity rocks. Rock Mech Rock Eng 45(4):607–617

    Google Scholar 

  62. Ji S, Karlovšek J (2021) Optimized differential evolution algorithm for solving DEM material calibration problem. Data Collection: The University of Queensland. https://doi.org/10.14264/ca1267d

Download references

Funding

Mr. Songtao Ji is grateful to the CSC (China Scholarship Council) and The University of Queensland for a Ph.D. fellowship.

Author information

Authors and Affiliations

  1. Geotechnical Engineering Centre, School of Civil Engineering, The University of Queensland, Brisbane, 4067, Australia

    Songtao Ji & Jurij Karlovšek

Authors
  1. Songtao Ji
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jurij Karlovšek
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Songtao Ji.

Ethics declarations

Conflict of interest

The authors have no relevant financial or non-financial interests to disclose.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ji, S., Karlovšek, J. Optimized differential evolution algorithm for solving DEM material calibration problem. Engineering with Computers 39, 2001–2016 (2023). https://doi.org/10.1007/s00366-021-01564-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-021-01564-8

Keywords