Skip to main content
Springer Nature Link
Log in

Analysis of the nanoscale heat transport and Lorentz force based on the time-dependent Cross nanofluid

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

A Correction to this article was published on 05 April 2022

This article has been updated

Abstract

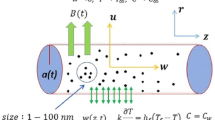
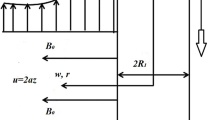
Control of transport of energy by means of external force effects is one of the most important problems in modern applied mathematics. Magnetic force has an influence on heat transport phenomena and has various applications in industrial, engineering, and medical sciences. The root theme of this work is to study MHD flow with stagnation point and flow of Cross nanofluid in contracting/extracting cylinder. The impacts of variable thermal conductivity, Lorentz’s force on unsteady Cross nanofluid and the cylindrical coordinate are investigated using the behavior of expanding/contracting cylinder. Discovering the impacts of physical parameters on movement, energy exchange and mass transport visibility of Cross nanofluid flow with respect to region (shear thinning/thickening) and on the basis of geometry (contracting/extracting) is most interesting and beauty of this attempt. Smooth debate on fluid behavior in light of numerical outcome classifying shear thinning/thickening and contracting/extracting of geometry is disclosed comprehensively. By keeping the idea of shooting methodology, the nonlinear higher order differential equations are converted into a first-order system of ordinary differential equations. Furthermore, bvp4c Matlab built-in command is used for comparison of the numerical solutions to solve these linear ordinary differential equations. The numerical solutions are plotted in figures as well as tabulated in some tables.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20

Similar content being viewed by others

Data availability statement

Data available on request from the authors.

Change history

Abbreviations

\(b_{0}\) :

Constant of dimension length \(t\)

\(K(T)\) :

Variable thermal conductivity

\(\beta\) :

Constant of contraction–expansion

\(U_{w} (x,t)\) :

Initial velocity

\(U_{e} (x,t)\) :

Free stream velocity

\(T_{w} ,C_{w}\) :

Temperature and concentration of cylinder

\(T_{\infty } ,C_{\infty }\) :

Temperature and concentration of cylinder

\(a,\,c\) :

Constant of dimension \(({\text{time}})^{ - 1}\)

\(\tau\) :

Cauchy stress tensor

\(k\) :

Thermal conductivity

\(x,\,\,r\) :

Space variable

\(s\) :

Suction parameter

\(k_{\infty }\) :

Conductivity away for

Pr :

Prandtl number

\(\xi\) :

Chemical rate reaction parameter

\(\lambda\) :

Velocity ratio parameter

\(\mu_{0}\) :

Zero shear rate viscosity

\(A_{1}\) :

First Rivilin–Erickson tensor

\(\mu_{\infty }\) :

Infinite shear rate viscosity

\(p\) :

Pressure

\(I\) :

Identity tensor

\(\Gamma\) :

Relaxation time constant

\(n\) :

Power law index

Sc:

Schmidt number

\(\mu\) :

Viscosity

\(q_{w}\) :

Wall shear stress

\(\tau_{rx \, }\) :

Heat flux

\(M\) :

Magnetic parameter

\(u,\,\,v\) :

Velocity component

\(c_{f}\) :

Skin friction

\(B_{0}\) :

Magnetic field strength constant

\(\mathop \gamma \limits^{.}\) :

Shear strain

\(B\) :

Magnetic field strength

\(c_{p}\) :

Specific heat

D:

Solute diffusivity

\(R_{r}\) :

Chemical reaction parameter

\(\sigma\) :

Reaction rate parameter

\(\rho\) :

Density

C:

Concentration profile

T:

Temperature profile

V:

Velocity profile

\(\theta_{w}\) :

Temperature ratio parameter

A:

Unsteadiness parameter

We:

Weissenberg

\(\alpha_{m}\) :

Thermal diffusivity

Re:

Reynolds number

Nu:

Nusselt number

References

  1. Choi SUS, Jeffrey AE (1995) Enhancing thermal conductivity of fluids with nanoparticles No. ANL/MSD/CP-84938; CONF-951135–29. In: Argonne National Lab., IL, United States

  2. Sheikholeslami M et al (2013) Application of LBM in simulation of natural convection in a nanofluid filled square cavity with curve boundaries. Powder Technol 247:87–94

    Google Scholar 

  3. Abolbashari MH et al (2014) Entropy analysis for an unsteady MHD flow pas a stretching permeable surface in nano-fluid. Powder Technol 267:256–267

    Google Scholar 

  4. Rashidi MM et al (2014) Comparative numerical study of single and two-phase models of nanofluid heat transfer in wavy channel. Appl Math Mech 35(7):831–848

    MathSciNet  Google Scholar 

  5. Freidoonimehr N, Mohammad MR, Shohel M (2015) Unsteady MHD free convective flow past a permeable stretching vertical surface in a nano-fluid. Int J Thermal Sci 87:136–145

    Google Scholar 

  6. Sabir Z, Ayub A, Guirao JL, Bhatti S, Shah SZH (2020) The effects of activation energy and thermophoretic diffusion of nanoparticles on steady micropolar fluid along with Brownian motion. Adv Mater Sci Eng. https://doi.org/10.1155/2020/2010568

    Article  Google Scholar 

  7. Mohamed MM, Mohamed RA, Wen-Xiu M (2021) A combined method for simulating MHD convection in square cavities through localized heating by method of line and penalty-artificial compressibility. Journal of Taibah University for Science 15(1):208–217. https://doi.org/10.1080/16583655.2021.1951503

    Article  Google Scholar 

  8. Shah SZ, Wahab HA, Ayub A, Sabir Z, Haider A, Shah SL (2021) Higher order chemical process with heat transport of magnetized cross nanofluid over wedge geometry. Heat Transfer 50(4):3196–3219

    Google Scholar 

  9. Baleanu D, Sadat R, Ali MR (2020) The method of lines for solution of the carbon nanotubes engine oil nanofluid over an unsteady rotating disk. Eur Phys J Plus 135:788. https://doi.org/10.1140/epjp/s13360-020-00763-4

    Article  Google Scholar 

  10. Ayub A, Wahab HA, Shah SZ, Shah SL, Darvesh A, Haider A, Sabir Z (2021) Interpretation of infinite shear rate viscosity and a nonuniform heat sink/source on a 3D radiative cross nanofluid with buoyancy assisting/opposing flow. Heat Transfer 50(5):4192–4232

    Google Scholar 

  11. Ayub A, Sabir Z, Altamirano GC, Sadat R, Ali MR (2021) Characteristics of melting heat transport of blood with time-dependent cross-nanofluid model using Keller-Box and BVP4C method. Eng Comput. https://doi.org/10.1007/s00366-021-01406-7

    Article  Google Scholar 

  12. Ayub A, Wahab HA, Hussain Shah SZ, Shah SL, et al (2021) On heated surface transport of heat bearing thermal radiation and MHD Cross flow with effects of nonuniform heat sink/source and buoyancy opposing/assisting flow. Heat Transfer 50(6):6110–6128

    Google Scholar 

  13. Jafari SS, Freidoonimehr N (2015) Second law of thermodynamics analysis of hydro-magnetic nano-fluid slip flow over a stretching permeable surface. J Braz Soc Mech Sci Eng 37(4):1245–1256

    Google Scholar 

  14. Bachok N, Ishak A, Pop I (2010) Boundary-layer flow of nanofluids over a moving surface in a flowing fluid. Int J Therm Sci 49(9):1663–1668

    Google Scholar 

  15. Rashidi MM et al (2014) Free convective heat and mass transfer for MHD fluid flow over a permeable vertical stretching sheet in the presence of the radiation and buoyancy effects. Ain Shams Eng J 5(3):901–912

    Google Scholar 

  16. Ayub A, Darvesh A, Altamirano GC, Sabir Z (2021) Nanoscale energy transport of inclined magnetized 3D hybrid nanofluid with Lobatto IIIA scheme. Heat Transfer. https://doi.org/10.1002/htj.22188

    Article  Google Scholar 

  17. Umar M, Akhtar R, Sabir Z, Wahab HA, Zhiyu Z, Imran A et al (2019) Numerical treatment for the three-dimensional eyring-powell fluid flow over a stretching sheet with velocity slip and activation energy. Adv Math Phys. https://doi.org/10.1155/2019/9860471

    Article  MathSciNet  MATH  Google Scholar 

  18. Umar M, Sabir Z, Imran A, Wahab AH, Shoaib M, Raja MAZ (2020) The 3-D flow of Casson nanofluid over a stretched sheet with chemical reactions, velocity slip, thermal radiation and Brownian motion. Therm Sci 24(5 Part A):2929–2939

    Google Scholar 

  19. Sabir Z, Imran A, Umar M, Zeb M, Shoaib M, Raja MAZ (2020) A numerical approach for two-dimensional Sutterby fluid flow bounded at a stagnation point with an inclined magnetic field and thermal radiation impacts. Therm Sci 00:186–186

    Google Scholar 

  20. Wu KJ et al (2015) Smartphone-enabled device for the monitoring of blood volume variations using magnetohydrodynamic voltages. Circulation 132(Suppl_3):A16689

    Google Scholar 

  21. Sheikholeslami M, Shehzad SA (2018) CVFEM simulation for nanofluid migration in a porous medium using Darcy model. Int J Heat Mass Transf 122:1264–1271

    Google Scholar 

  22. Sheikholeslami M, Li Z, Shamlooei M (2018) Nanofluid MHD natural convection through a porous complex shaped cavity considering thermal radiation. Phys Lett A 382(24):1615–1632

    MathSciNet  Google Scholar 

  23. Abdulhameed M, Vieru D, Roslan R (2017) Modeling electro-magneto-hydrodynamic thermo-fluidic transport of biofluids with new trend of fractional derivative without singular kernel. Physica A 484:233–252

    MathSciNet  MATH  Google Scholar 

  24. Brusentsov NA et al (2007) Magnetohydrodynamic thermochemotherapy and MRI of mouse tumors. J Magnet Magnet Mater 311(1):176–180

    Google Scholar 

  25. Brusentsov NA et al (2012) Magnetohydrodynamic thermochemotherapy and MRI of malignant tumorigenesis. Solid State Phenom 190:717–720 (Trans Tech Publications)

    Google Scholar 

  26. Brusentsov NA et al (2008) Magnetohydrodynamic thermochemotherapy of malignant tumors with nanopreparations with magnetic resonance monitoring. Pharm Chem J 42(4):157–164

    Google Scholar 

  27. Sheikholeslami M, Mollabasi H, Ganji DD (2015) Analytical investigation of MHD Jeffery-Hamel nanofluid flow in non-parallel walls. Int J Nanosci Nanotechnol 11(4):241–248

    Google Scholar 

  28. Severo DS et al (2005) Modeling magnetohydrodynamics of aluminum electrolysis cells with ANSYS and CFX. Light Metals 2005:475–480

    Google Scholar 

  29. Steg L., Sutton GW (1960) The prospects of MHD power generation. Astronautics 5:158–174

    Google Scholar 

  30. Scannell EP (1980) Gaseous electrode for MHD generator. U.S. Patent No. 4,185,213

  31. Brogan TR and Powers Jr WE (1969) Magnetohydrodynamic motor-generator. U.S. Patent No. 3,436,918

  32. Micci MM, Caveny LH (1982) MHD measurement of acoustic velocities in rocket motor chambers. AIAA J 20(4):516–521

    Google Scholar 

  33. Davidson PA (1999) Magnetohydrodynamics in materials processing. Annu Rev Fluid Mech 31(1):273–300

    Google Scholar 

  34. Pu ZY et al (1997) MHD drift ballooning instability near the inner edge of the near-Earth plasma sheet and its application to substorm onset. J Geophys Res Space Phys 102(A7):14397–14406

    Google Scholar 

  35. Ghiasi M et al (2011) Psoriasis and increased prevalence of hypertension and diabetes mellitus. Indian J Dermatol 56(5):533

    Google Scholar 

  36. Zohdi M et al (2012) Data envelopment analysis (DEA) based performance evaluation system for investment companies: case study of Tehran Stock Exchange. Afr J Bus Manage 6(16):5573–5577

    Google Scholar 

  37. Raftari B, Yildirim A (2010) The application of homotopy perturbation method for MHD flows of UCM fluids above porous stretching sheets. Comput Math Appl 59(10):3328–3337

    MathSciNet  MATH  Google Scholar 

  38. Mahapatra TR, Nandy SK, Gupta AS (2009) Magnetohydrodynamic stagnation-point flow of a power-law fluid towards a stretching surface. Int J Non-Linear Mech 44(2):124–129

    MATH  Google Scholar 

  39. Bhattacharyya S, Gupta AS (1998) MHD flow and heat transfer at a general three-dimensional stagnation point. Int J Non-Linear Mech 33(1):125–134

    MATH  Google Scholar 

  40. Esfe MH et al (2015) An experimental study on the effect of diameter on thermal conductivity and dynamic viscosity of Fe/water nanofluids. J Therm Anal Calorim 119(3):1817–1824

    MathSciNet  Google Scholar 

  41. Nandy SK, Mahapatra TR (2013) Effects of slip and heat generation/absorption on MHD stagnation flow of nanofluid past a stretching/shrinking surface with convective boundary conditions. Int J Heat Mass Transfer 64:1091–1100

    Google Scholar 

  42. El-Kabeir SMM et al (2019) Unsteady MHD slip flow of a ferrofluid over an impulsively stretched vertical surface. AIP Adv 9(4):045112

    Google Scholar 

  43. Pekmen B, Tezer-Sezgin M (2015) DRBEM solution of MHD flow with magnetic induction and heat transfer. Comput Model Eng Sci 105(3):183–207

    MATH  Google Scholar 

  44. Das S, Jana RN, Makinde OD (2015) Magnetohydrodynamic mixed convective slip flow over an inclined porous plate with viscous dissipation and Joule heating. Alex Eng J 54(2):251–261

    Google Scholar 

  45. Singh G, Makinde OD (2015) Mixed convection slip flow with temperature jump along a moving plate in presence of free stream. Therm Sci 19(1):119–128

    Google Scholar 

  46. Sabir Z, Akhtar R, Zhiyu Z, Umar M, Imran A, Wahab HA, Shoaib M, Raja MAZ (2019) A computational analysis of two-phase casson nanofluid passing a stretching sheet using chemical reactions and gyrotactic microorganisms. Math Prob Eng. https://doi.org/10.1155/2019/1490571

    Article  MathSciNet  MATH  Google Scholar 

  47. Sabir Z, Imran A, Umar M, Zeb M, Shoaib M, Zahoor Raja MA (2021) A numerical approach for 2-D Sutterby fluid-flow bounded at a stagnation point with an inclined magnetic field and thermal radiation impacts. Therm Sci 25:1975–1987

    Google Scholar 

  48. Domairry G, Aziz A (2009) Approximate analysis of MHD squeeze flow between two parallel disks with suction or injection by homotopy perturbation method. Math Prob Eng. https://doi.org/10.1155/2009/603916

    Article  MATH  Google Scholar 

  49. Sheikholeslami M, Abelman S, Ganji DD (2014) Numerical simulation of MHD nanofluid flow and heat transfer considering viscous dissipation. Int J Heat Mass Transfer 79:212–222

    Google Scholar 

  50. Zhang J-K, Li B-W, Chen Y-Y (2013) Hall effects on natural convection of participating MHD with thermal radiation in a cavity. Int J Heat Mass Transf 66:838–843

    Google Scholar 

  51. Ali MR (2021) The method of lines analysis of heat transfer of Ostwald-de Waele fluid generated by a non-uniform rotating disk with a variable thickness. J Appl Comput Mech 7(2):432–441

    Google Scholar 

  52. Srinivas S, Malathy T, Subramanyam Reddy A (2016) A note on thermal-diffusion and chemical reaction effects on MHD pulsating flow in a porous channel with slip and convective boundary conditions. J King Saud Univ-Eng Sci 28(2):213–221

    Google Scholar 

  53. Swapna G et al (2015) Finite element modeling of a double-diffusive mixed convection flow of a chemically-reacting magneto-micropolar fluid with convective boundary condition. J Taiwan Inst Chem Eng 47:18–27

    Google Scholar 

  54. Mabood F, Khan WA, Md Ismail AI (2015) MHD stagnation point flow and heat transfer impinging on stretching sheet with chemical reaction and transpiration. Chem Eng J 273:430–437

    Google Scholar 

  55. Hayat T et al (2017) Mixed convection stagnation-point flow of Powell-Eyring fluid with Newtonian heating, thermal radiation, and heat generation/absorption. J Aerosp Eng 30(1):04016077

    Google Scholar 

  56. Narayana PVS, Harish Babu D (2016) Numerical study of MHD heat and mass transfer of a Jeffrey fluid over a stretching sheet with chemical reaction and thermal radiation. J Taiwan Inst Chem Eng 59:18–25

    Google Scholar 

  57. Kuang Z-B (2015) Energy and entropy equations in coupled nonequilibrium thermal mechanical diffusive chemical heterogeneous system. Sci Bull 60(10):952–957

    Google Scholar 

  58. Mason EA, Marrero TR (1970) The diffusion of atoms and molecules. Adv Atom Mol Phys 6:155–232 (Academic Press)

    Google Scholar 

  59. Demirel Y (2009) Thermodynamically coupled heat and mass flows in a reaction-transport system with external resistances. Int J Heat Mass Transf 52(7–8):2018–2025

    MATH  Google Scholar 

  60. Deen WM (1998) Analysis of transport phenomena. New York: Oxford university press

    Google Scholar 

  61. Flytzani-Stephanopoulos M, Schmidt LD (1979) Morphology and etching processes on macroscopic metal catalysts. Prog Surf Sci 9(3):83–111

    Google Scholar 

  62. Ortiz de Zárate JM et al (2007) Concentration fluctuations in nonisothermal reaction-diffusion systems. J Chem Phys 127(3):034501

    Google Scholar 

  63. Hu S, Shen S (2013) Non-equilibrium thermodynamics and variational principles for fully coupled thermal–mechanical–chemical processes. Acta Mech 224(12):2895–2910

    MathSciNet  MATH  Google Scholar 

  64. Azam M, Khan M, Alshomrani AS (2017) Unsteady radiative stagnation point flow of MHD Carreau nanofluid over expanding/contracting cylinder. Int J Mech Sci 130:64–73

    Google Scholar 

  65. Lok YY, Pop I (2011) Wang’s shrinking cylinder problem with suction near a stagnation point. Phys Fluids 23(8):083102

    MATH  Google Scholar 

  66. Yusuf A, Sulaiman TA, Inc M, Bayram M (2020) Breather wave, lump-periodic solutions and some other interaction phenomena to the Caudrey–Dodd–Gibbon equation. Eur Phys J Plus 135(7):1–8

    Google Scholar 

  67. Abdel-Gawad HI, Tantawy M, Inc M, Yusuf A (2020) Construction of rogue waves and conservation laws of the complex coupled Kadomtsev-Petviashvili equation. Int J Mod Phys B 34(12):2050115

    MathSciNet  MATH  Google Scholar 

  68. Yusuf A, Tchier F, Inc M (2020) New interaction and combined multi-wave solutions for the Heisenberg ferromagnetic spin chain equation. Eur Phys J Plus 135(5):1–8

    Google Scholar 

  69. Wang S, Yousefpour A, Yusuf A, Jahanshahi H, Alcaraz R, He S, Munoz-Pacheco JM (2020) Synchronization of a non-equilibrium four-dimensional chaotic system using a disturbance-observer-based adaptive terminal sliding mode control method. Entropy 22(3):271

    MathSciNet  Google Scholar 

  70. Singh S, Sakthivel R, Inc M, Yusuf A, Murugesan K (2020) Dynamics of optical solitons and conservation laws of a new (2+ 1)-dimensional integrable nonlinear evolution equation in deep water oceanic waves. Mod Phys Lett B 34(05):2050068

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, Hazara University, Manshera, Pakistan

    Assad Ayub, Zulqurnain sabir & Hafiz A. Wahab

  2. Department of Industrial Engineering, Faculty of Engineering, King Abdulaziz University, Jeddah, Saudi Arabia

    Mohammed Balubaid

  3. GRC Department, Faculty of Applied Studies, King Abdulaziz University, Jeddah, Saudi Arabia

    S. R. Mahmoud

  4. Faculty of Engineering and Technology, Future University, Cairo, Egypt

    Mohamed R. Ali

  5. Department of Basic Science, Faculty of Engineering at Benha, Benha University, Benha, 13512, Egypt

    Mohamed R. Ali

  6. Department of Physics and Engineering Mathematics, Faculty of Engineering, Zagazig University, Zagazig, Egypt

    R. Sadat

Authors
  1. Assad Ayub
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Zulqurnain sabir
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Hafiz A. Wahab
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Mohammed Balubaid
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. S. R. Mahmoud
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Mohamed R. Ali
    View author publications

    You can also search for this author inPubMed Google Scholar

  7. R. Sadat
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Mohamed R. Ali.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ayub, A., sabir, Z., Wahab, H.A. et al. Analysis of the nanoscale heat transport and Lorentz force based on the time-dependent Cross nanofluid. Engineering with Computers 39, 2089–2108 (2023). https://doi.org/10.1007/s00366-021-01579-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-021-01579-1

Keywords