Skip to main content
Springer Nature Link
Log in

A new iterative technique for solving fractal-fractional differential equations based on artificial neural network in the new generalized Caputo sense

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

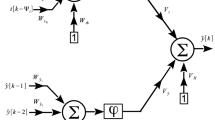
This paper attempts to create an artificial neural networks (ANNs) technique for solving well-known fractal-fractional differential equations (FFDEs). FFDEs have the advantage of being able to help explain a variety of real-world physical problems. The technique implemented in this paper converts the original differential equation into a minimization problem using a suggested truncated power series of the solution function. Next, answer to the problem is obtained via computing the parameters with highly precise neural network model. We can get a good approximate solution of FFDEs by combining the initial conditions with the ANNs performance. Examples are provided to portray the efficiency and applicability of this method. Comparison with similar existing approaches are also conducted to demonstrate the accuracy of the proposed approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Jain S, Agarwal P (2012) On applications of fractional calculus involving summations of series. In: Applied mathematics & approximation theory, May 17–20, 2012–Ankara–Turkey, p 96

  2. Metzler R, Klafter J (2000) The random walks guide to anomalous diffusion: a fractional dynamics approach. Phys Rep 339(1):1–77

    Article  MathSciNet  MATH  Google Scholar 

  3. Baleanu D, Güvenç ZB, Machado T et al (2010) New trends in nanotechnology and fractional calculus applications. Springer, Berlin

    Book  MATH  Google Scholar 

  4. Mohammed PO, Abdeljawad T, Baleanu D, Kashuri A, Hamasalh F, Agarwal P (2020) New fractional inequalities of Hermite-Hadamard type involving the incomplete gamma functions. J Inequalities Appl 2020(1):1–16

    MathSciNet  MATH  Google Scholar 

  5. Bagley Ronald L, Torvik P (1984) On the appearence of the fractional derivative in the behavior of real materials. J Appl Mech 51. https://doi.org/10.1115/1.3167615

  6. Baleanu D, Diethelm K, Scalas E, Trujillo JJ (2012) Fractional calculus: models and numerical methods, vol 3. World Scientific, Singapore

    MATH  Google Scholar 

  7. Valério D, Machado JT, Kiryakova V (2014) Some pioneers of the applications of fractional calculus. Fract Calc Appl Anal 17(2):552–578

    Article  MathSciNet  MATH  Google Scholar 

  8. Atangana A (2017) Fractal-fractional differentiation and integration: connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 102:396–406

    Article  MathSciNet  MATH  Google Scholar 

  9. Shloof A, Senu N, Ahmadian A, Salahshour S (2021) An efficient operation matrix method for solving fractal-fractional differential equations with generalized caputo-type fractional-fractal derivative. Math Comput Simul 188:415–435

    Article  MathSciNet  MATH  Google Scholar 

  10. Pakdaman M, Ahmadian A, Effati S, Salahshour S, Baleanu D (2017) Solving differential equations of fractional order using an optimization technique based on training artificial neural network. Appl Math Comput 293:81–95

    MathSciNet  MATH  Google Scholar 

  11. Zúñiga-Aguilar CJ, Romero-Ugalde HM, Gómez-Aguilar JF, Escobar-Jiménez RF, Valtierra-Rodríguez M (2017) Solving fractional differential equations of variable-order involving operators with Mittag-Leffler kernel using artificial neural networks. Chaos Solitons Fractals 103:382–403

    Article  MathSciNet  MATH  Google Scholar 

  12. Jafarian A, Rostami F, Golmankhaneh AK, Baleanu D (2017) Using ANNs approach for solving fractional order Volterra integro-differential equations. International Journal of Computational Intelligence Systems 10(1):470–480

    Article  Google Scholar 

  13. Chakraverty S, Mall S (2014) Regression-based weight generation algorithm in neural network for solution of initial and boundary value problems. Neural Comput Appl 25(3):585–594

    Article  Google Scholar 

  14. Mall S, Chakraverty S (2016) Application of legendre neural network for solving ordinary differential equations. Appl Soft Comput 43:347–356

    Article  Google Scholar 

  15. Mall S, Chakraverty S (2016) Hermite functional link neural network for solving the van der pol-duffing oscillator equation. Neural Comput 28(8):1574–1598

    Article  MathSciNet  MATH  Google Scholar 

  16. Mall S, Chakraverty S (2014) Chebyshev neural network based model for solving Lane-Emden type equations. Appl Math Comput 247:100–114

    MathSciNet  MATH  Google Scholar 

  17. Jafarian A, Mokhtarpour M, Baleanu D (2017) Artificial neural network approach for a class of fractional ordinary differential equation. Neural Comput Appl 28(4):765–773

    Article  Google Scholar 

  18. Rostami F, Jafarian A (2018) A new artificial neural network structure for solving high-order linear fractional differential equations. Int J Comput Math 95(3):528–539

    Article  MathSciNet  MATH  Google Scholar 

  19. Anitescu C, Atroshchenko E, Alajlan N, Rabczuk T (2019) Artificial neural network methods for the solution of second order boundary value problems. Comput Mater Contin 59(1):345–359

    Google Scholar 

  20. Liu B, Vu-Bac N, Rabczuk T (2021) A stochastic multiscale method for the prediction of the thermal conductivity of polymer nanocomposites through hybrid machine learning algorithms. Compos Struct 273:114269

    Article  Google Scholar 

  21. Samaniego E, Anitescu C, Goswami S, Nguyen-Thanh VM, Guo H, Hamdia K, Zhuang X, Rabczuk T (2020) An energy approach to the solution of partial differential equations in computational mechanics via machine learning: concepts, implementation and applications. Comput Methods Appl Mech Eng 362:112790

    Article  MathSciNet  MATH  Google Scholar 

  22. Zhuang X, Guo H, Alajlan N, Zhu H, Rabczuk T (2021) Deep autoencoder based energy method for the bending, vibration, and buckling analysis of Kirchhoff plates with transfer learning. Eur J Mech A Solids 87:104225

    Article  MathSciNet  MATH  Google Scholar 

  23. Guo H, Zhuang X, Rabczuk T (2021) A deep collocation method for the bending analysis of Kirchhoff plate. arXiv preprint https://arxiv.org/abs/2102.02617

  24. Zúñiga-Aguilar CJ, Gómez-Aguilar JF, Romero-Ugalde HM, Jahanshahi H, Alsaadi FE (2021) Fractal-fractional neuro-adaptive method for system identification. Eng Comput 1–24. https://doi.org/10.1007/s00366-021-01314-w

  25. Graupe D (2013) Principles of artificial neural networks, vol 7. World Scientific, Singapore

    MATH  Google Scholar 

  26. Hanss M (2005) Applied fuzzy arithmetic. Springer, Berlin

    MATH  Google Scholar 

  27. El-Ajou A, Arqub OA, Zhour ZA, Momani S (2013) New results on fractional power series: theories and applications. Entropy 15(12):5305–5323

    Article  MathSciNet  MATH  Google Scholar 

  28. Jumarie G (2006) Modified Riemann-Liouville derivative and fractional Taylor series of nondifferentiable functions further results. Comput Math Appl 51(9–10):1367–1376

    Article  MathSciNet  MATH  Google Scholar 

  29. Hornik K, Stinchcombe M, White H (1989) Multilayer feedforward networks are universal approximators. Neural Netw 2(5):359–366

    Article  MATH  Google Scholar 

  30. Funahashi K-I (1989) On the approximate realization of continuous mappings by neural networks. Neural Netw 2(3):183–192

    Article  Google Scholar 

  31. Mall S, Chakraverty S (2018) Artificial neural network approach for solving fractional order initial value problems. arXiv preprint https://arxiv.org/1810.04992

  32. Sakar MG, Akgül A, Baleanu D (2017) On solutions of fractional Riccati differential equations. Adv Differ Equ 2017(1):1–10

    Article  MathSciNet  MATH  Google Scholar 

  33. Lodhi S, Manzar MA, Raja MAZ (2019) Fractional neural network models for nonlinear Riccati systems. Neural Comput Appl 31(1):359–378

    Article  Google Scholar 

  34. Saratha SR, Bagyalakshmi M, Krishnan SS (2020) Fractional generalised homotopy analysis method for solving nonlinear fractional differential equations. Comput Appl Math 39(2):1–32

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, Universiti Putra Malaysia, Serdang, Selangor, Malaysia

    A. M. Shloof & N. Senu

  2. Institute for Mathematical Research, Universiti Putra Malaysia, Serdang, Selangor, Malaysia

    N. Senu

  3. Department of Mathematics, Faculty of Science, Al-Zintan University, Alzintan, Libya

    A. M. Shloof

  4. Department of Law, Economics and Human Sciences, Mediterranea University of Reggio Calabria, Reggio Calabria, Italy

    A. Ahmadian

  5. Department of Mathematics, Near East University, TRNC, Mersin 10, Nicosia, Turkey

    A. Ahmadian

  6. Atmospheric Science and Meteorological Research Center (ASMERC), Climatological Research Institute (CRI), Mashhad, Iran

    M. Pakdaman

  7. Faculty of Engineering and Natural Sciences, Bahcesehir University, Istanbul, Turkey

    S. Salahshour

Authors
  1. A. M. Shloof
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. N. Senu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. A. Ahmadian
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. M. Pakdaman
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. S. Salahshour
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding authors

Correspondence to N. Senu or A. Ahmadian.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shloof, A.M., Senu, N., Ahmadian, A. et al. A new iterative technique for solving fractal-fractional differential equations based on artificial neural network in the new generalized Caputo sense. Engineering with Computers 39, 505–515 (2023). https://doi.org/10.1007/s00366-022-01607-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-022-01607-8

Keywords