Skip to main content
Springer Nature Link
Log in

Nonlinear forced vibrations of three-phase nanocomposite shells considering matrix rheological behavior and nano-fiber waviness

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

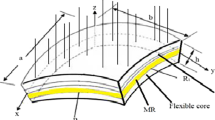
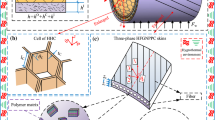
The present study investigates the nonlinear vibrations in thin-walled shells consisting of three-phase polymer nanocomposites with regard to the viscoelastic properties of polymer and curved shape of carbon nanotubes (CNTs). To this end, a hierarchical micromechanical framework is introduced to study the effective properties of multi-scale hybrid (MSH) nanocomposite. Next, the von Kármán-type nonlinearity is considered together with the displacement field of the classical shell theory to derive the governing equations in the context of Hamilton’s principle. In addition, the impacts of both axial compression and transverse harmonic stimulation on the dynamic response of the system are taken into consideration. Afterward, the method of harmonic balance is implemented to find the frequency–response relation of the structure. The transient response is also achieved with the aid of fourth-order Runge–Kutta method. The results of this work reveal that resonance estimation in such hybrid nanomaterial structures will be inaccurate if the softening effect of waviness phenomenon on the modulus is ignored. On one hand, it is demonstrated that the amplitude of the dynamic deflection of the shell will be reduced with time (i.e., due to the viscoelastic properties of the polymer). On the other hand, it is depicted that rising the content of glass fibers (GFs) in the MSH nanocomposite shell results in softer oscillations. The reason for this trend is the reducing impact of this change on the content of the CNTs in the composition of the polymer nanocomposite.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Iijima S (1991) Helical microtubules of graphitic carbon. Nature 354(6348):56–58. https://doi.org/10.1038/354056a0

    Article  Google Scholar 

  2. Ruoff RS, Lorents DC (1995) Mechanical and thermal properties of carbon nanotubes. Carbon 33(7):925–930. https://doi.org/10.1016/0008-6223(95)00021-5

    Article  Google Scholar 

  3. Xie S, Li W, Pan Z, Chang B, Sun L (2000) Mechanical and physical properties on carbon nanotube. J Phys Chem Solids 61(7):1153–1158. https://doi.org/10.1016/S0022-3697(99)00376-5

    Article  Google Scholar 

  4. Ajayan PM, Stephan O, Colliex C, Trauth D (1994) Aligned carbon nanotube arrays formed by cutting a polymer resin—nanotube composite. Science 265(5176):1212–1214. https://doi.org/10.1126/science.265.5176.1212

    Article  Google Scholar 

  5. Shen H-S, Zhang C-L (2010) Thermal buckling and postbuckling behavior of functionally graded carbon nanotube-reinforced composite plates. Mater Des 31(7):3403–3411. https://doi.org/10.1016/j.matdes.2010.01.048

    Article  Google Scholar 

  6. Shen H-S (2011) Postbuckling of nanotube-reinforced composite cylindrical shells in thermal environments. Part II: Pressure-loaded shells Composite Structures 93(10):2496–2503. https://doi.org/10.1016/j.compstruct.2011.04.005

    Article  Google Scholar 

  7. Wang Z-X, Shen H-S (2011) Nonlinear vibration of nanotube-reinforced composite plates in thermal environments. Comput Mater Sci 50(8):2319–2330. https://doi.org/10.1016/j.commatsci.2011.03.005

    Article  Google Scholar 

  8. Shen H-S, Xiang Y (2012) Nonlinear vibration of nanotube-reinforced composite cylindrical shells in thermal environments. Comput Methods Appl Mech Eng 213–216:196–205. https://doi.org/10.1016/j.cma.2011.11.025

    Article  MathSciNet  MATH  Google Scholar 

  9. Wang Z-X, Shen H-S (2012) Nonlinear dynamic response of nanotube-reinforced composite plates resting on elastic foundations in thermal environments. Nonlinear Dyn 70(1):735–754. https://doi.org/10.1007/s11071-012-0491-2

    Article  MathSciNet  Google Scholar 

  10. Zhu P, Lei ZX, Liew KM (2012) Static and free vibration analyses of carbon nanotube-reinforced composite plates using finite element method with first order shear deformation plate theory. Compos Struct 94(4):1450–1460. https://doi.org/10.1016/j.compstruct.2011.11.010

    Article  Google Scholar 

  11. Lei ZX, Liew KM, Yu JL (2013) Large deflection analysis of functionally graded carbon nanotube-reinforced composite plates by the element-free kp-Ritz method. Comput Methods Appl Mech Eng 256:189–199. https://doi.org/10.1016/j.cma.2012.12.007

    Article  MathSciNet  MATH  Google Scholar 

  12. Rafiee M, Yang J, Kitipornchai S (2013) Thermal bifurcation buckling of piezoelectric carbon nanotube reinforced composite beams. Comput Math Appl 66(7):1147–1160. https://doi.org/10.1016/j.camwa.2013.04.031

    Article  MATH  Google Scholar 

  13. Rafiee M, Yang J, Kitipornchai S (2013) Large amplitude vibration of carbon nanotube reinforced functionally graded composite beams with piezoelectric layers. Compos Struct 96:716–725. https://doi.org/10.1016/j.compstruct.2012.10.005

    Article  Google Scholar 

  14. Ansari R, Faghih Shojaei M, Mohammadi V, Gholami R, Sadeghi F (2014) Nonlinear forced vibration analysis of functionally graded carbon nanotube-reinforced composite Timoshenko beams. Compos Struct 113:316–327. https://doi.org/10.1016/j.compstruct.2014.03.015

    Article  Google Scholar 

  15. Heydarpour Y, Aghdam MM, Malekzadeh P (2014) Free vibration analysis of rotating functionally graded carbon nanotube-reinforced composite truncated conical shells. Compos Struct 117:187–200. https://doi.org/10.1016/j.compstruct.2014.06.023

    Article  MATH  Google Scholar 

  16. Rafiee M, He XQ, Liew KM (2014) Non-linear dynamic stability of piezoelectric functionally graded carbon nanotube-reinforced composite plates with initial geometric imperfection. Int J Non-Linear Mech 59:37–51. https://doi.org/10.1016/j.ijnonlinmec.2013.10.011

    Article  Google Scholar 

  17. Shen H-S, Xiang Y (2014) Postbuckling of axially compressed nanotube-reinforced composite cylindrical panels resting on elastic foundations in thermal environments. Compos B Eng 67:50–61. https://doi.org/10.1016/j.compositesb.2014.06.020

    Article  Google Scholar 

  18. Shen H-S, Xiang Y (2014) Nonlinear vibration of nanotube-reinforced composite cylindrical panels resting on elastic foundations in thermal environments. Compos Struct 111:291–300. https://doi.org/10.1016/j.compstruct.2014.01.010

    Article  Google Scholar 

  19. Zhang LW, Song ZG, Liew KM (2015) Nonlinear bending analysis of FG-CNT reinforced composite thick plates resting on Pasternak foundations using the element-free IMLS-Ritz method. Compos Struct 128:165–175. https://doi.org/10.1016/j.compstruct.2015.03.011

    Article  Google Scholar 

  20. Duc ND, Cong PH, Tuan ND, Tran P, Thanh NV (2017) Thermal and mechanical stability of functionally graded carbon nanotubes (FG CNT)-reinforced composite truncated conical shells surrounded by the elastic foundations. Thin-Walled Structures 115:300–310. https://doi.org/10.1016/j.tws.2017.02.016

    Article  Google Scholar 

  21. Duc ND, Lee J, Nguyen-Thoi T, Thang PT (2017) Static response and free vibration of functionally graded carbon nanotube-reinforced composite rectangular plates resting on Winkler-Pasternak elastic foundations. Aerosp Sci Technol 68:391–402. https://doi.org/10.1016/j.ast.2017.05.032

    Article  Google Scholar 

  22. Ebrahimi F, Farazmandnia N (2017) Thermo-mechanical vibration analysis of sandwich beams with functionally graded carbon nanotube-reinforced composite face sheets based on a higher-order shear deformation beam theory. Mech Adv Mater Struct 24(10):820–829. https://doi.org/10.1080/15376494.2016.1196786

    Article  Google Scholar 

  23. Memar Ardestani M, Zhang LW, Liew KM (2017) Isogeometric analysis of the effect of CNT orientation on the static and vibration behaviors of CNT-reinforced skew composite plates. Comput Methods Appl Mech Eng 317:341–379. https://doi.org/10.1016/j.cma.2016.12.009

    Article  MathSciNet  MATH  Google Scholar 

  24. Civalek Ö, Baltacıoğlu AK (2018) Vibration of carbon nanotube reinforced composite (CNTRC) annular sector plates by discrete singular convolution method. Compos Struct 203:458–465. https://doi.org/10.1016/j.compstruct.2018.07.037

    Article  Google Scholar 

  25. Kiani Y, Mirzaei M (2018) Rectangular and skew shear buckling of FG-CNT reinforced composite skew plates using Ritz method. Aerosp Sci Technol 77:388–398. https://doi.org/10.1016/j.ast.2018.03.022

    Article  Google Scholar 

  26. Moradi-Dastjerdi R, Aghadavoudi F (2018) Static analysis of functionally graded nanocomposite sandwich plates reinforced by defected CNT. Compos Struct 200:839–848. https://doi.org/10.1016/j.compstruct.2018.05.122

    Article  Google Scholar 

  27. Thai CH, Ferreira AJM, Rabczuk T, Nguyen-Xuan H (2018) A naturally stabilized nodal integration meshfree formulation for carbon nanotube-reinforced composite plate analysis. Eng Anal Boundary Elem 92:136–155. https://doi.org/10.1016/j.enganabound.2017.10.018

    Article  MathSciNet  MATH  Google Scholar 

  28. Ansari R, Torabi J, Hassani R (2019) A comprehensive study on the free vibration of arbitrary shaped thick functionally graded CNT-reinforced composite plates. Eng Struct 181:653–669. https://doi.org/10.1016/j.engstruct.2018.12.049

    Article  Google Scholar 

  29. Chakraborty S, Dey T, Kumar R (2019) Stability and vibration analysis of CNT-Reinforced functionally graded laminated composite cylindrical shell panels using semi-analytical approach. Compos B Eng 168:1–14. https://doi.org/10.1016/j.compositesb.2018.12.051

    Article  Google Scholar 

  30. Jiao P, Chen Z, Li Y, Ma H, Wu J (2019) Dynamic buckling analyses of functionally graded carbon nanotubes reinforced composite (FG-CNTRC) cylindrical shell under axial power-law time-varying displacement load. Compos Struct 220:784–797. https://doi.org/10.1016/j.compstruct.2019.04.048

    Article  Google Scholar 

  31. Khosravi S, Arvin H, Kiani Y (2019) Interactive thermal and inertial buckling of rotating temperature-dependent FG-CNT reinforced composite beams. Compos B Eng 175:107178. https://doi.org/10.1016/j.compositesb.2019.107178

    Article  Google Scholar 

  32. Mehar K, Panda SK (2019) Theoretical deflection analysis of multi-walled carbon nanotube reinforced sandwich panel and experimental verification. Compos B Eng 167:317–328. https://doi.org/10.1016/j.compositesb.2018.12.058

    Article  Google Scholar 

  33. Bendenia N, Zidour M, Bousahla AA, Bourada F, Tounsi A, Benrahou KH, Bedia EAA, Mahmoud SR, Tounsi A (2020) Deflections, stresses and free vibration studies of FG-CNT reinforced sandwich plates resting on Pasternak elastic foundation. Comput Concr 26(3):213–226. https://doi.org/10.12989/cac.2020.26.3.213

    Article  Google Scholar 

  34. Civalek Ö, Avcar M (2020) Free vibration and buckling analyses of CNT reinforced laminated non-rectangular plates by discrete singular convolution method. Eng Comput. https://doi.org/10.1007/s00366-020-01168-8

    Article  Google Scholar 

  35. Moradi-Dastjerdi R, Behdinan K, Safaei B, Qin Z (2020) Buckling behavior of porous CNT-reinforced plates integrated between active piezoelectric layers. Eng Struct 222:111141. https://doi.org/10.1016/j.engstruct.2020.111141

    Article  Google Scholar 

  36. Ebrahimi F, Farazmandnia N, Kokaba MR, Mahesh V (2021) Vibration analysis of porous magneto-electro-elastically actuated carbon nanotube-reinforced composite sandwich plate based on a refined plate theory. Eng Comput 37(2):921–936. https://doi.org/10.1007/s00366-019-00864-4

    Article  Google Scholar 

  37. Zerrouki R, Karas A, Zidour M, Bousahla AA, Tounsi A, Bourada F, Tounsi A, Benrahou KH, Mahmoud SR (2021) Effect of nonlinear FG-CNT distribution on mechanical properties of functionally graded nano-composite beam. Struct Eng Mech 78(2):117–124. https://doi.org/10.12989/sem.2021.78.2.117

    Article  Google Scholar 

  38. Ghorbanpour Arani A, Kiani F, Afshari H (2021) Free and forced vibration analysis of laminated functionally graded CNT-reinforced composite cylindrical panels. J Sandwich Struct Mater 23(1):255–278. https://doi.org/10.1177/1099636219830787

    Article  Google Scholar 

  39. Zhang YY, Wang YX, Zhang X, Shen HM, She G-L (2021) On snap-buckling of FG-CNTR curved nanobeams considering surface effects. Steel Compos Struct 38(3):293–304. https://doi.org/10.12989/scs.2021.38.3.293

    Article  Google Scholar 

  40. Heidari F, Taheri K, Sheybani M, Janghorban M, Tounsi A (2021) On the mechanics of nanocomposites reinforced by wavy/defected/aggregated nanotubes. Steel Compos Struct 38(5):533–545. https://doi.org/10.12989/scs.2021.38.5.533

    Article  Google Scholar 

  41. Huang Y, Karami B, Shahsavari D, Tounsi A (2021) Static stability analysis of carbon nanotube reinforced polymeric composite doubly curved micro-shell panels. Archives Civ Mech Eng 21(4):139. https://doi.org/10.1007/s43452-021-00291-7

    Article  Google Scholar 

  42. Arshid E, Khorasani M, Soleimani-Javid Z, Amir S, Tounsi A (2021) Porosity-dependent vibration analysis of FG microplates embedded by polymeric nanocomposite patches considering hygrothermal effect via an innovative plate theory. Eng Comput. https://doi.org/10.1007/s00366-021-01382-y

    Article  Google Scholar 

  43. Zhang M, Li J (2009) Carbon nanotube in different shapes. Mater Today 12(6):12–18. https://doi.org/10.1016/S1369-7021(09)70176-2

    Article  Google Scholar 

  44. Ebrahimi F, Dabbagh A (2020) A brief review on the influences of nanotubes' entanglement and waviness on the mechanical behaviors of CNTR polymer nanocomposites. Journal of Computational Applied Mechanics 51 (1):247–252. Doi: https://doi.org/10.22059/jcamech.2020.304476.517

  45. Arasteh R, Omidi M, Rousta AHA, Kazerooni H (2011) A study on effect of waviness on mechanical properties of multi-walled carbon nanotube/epoxy composites using modified halpin-tsai theory. J Macromol Sci Part B 50(12):2464–2480. https://doi.org/10.1080/00222348.2011.579868

    Article  Google Scholar 

  46. Tornabene F, Fantuzzi N, Bacciocchi M, Viola E (2016) Effect of agglomeration on the natural frequencies of functionally graded carbon nanotube-reinforced laminated composite doubly-curved shells. Compos B Eng 89:187–218. https://doi.org/10.1016/j.compositesb.2015.11.016

    Article  Google Scholar 

  47. Bacciocchi M, Tarantino AM (2019) Time-dependent behavior of viscoelastic three-phase composite plates reinforced by Carbon nanotubes. Compos Struct 216:20–31. https://doi.org/10.1016/j.compstruct.2019.02.083

    Article  Google Scholar 

  48. Rafiee M, Liu XF, He XQ, Kitipornchai S (2014) Geometrically nonlinear free vibration of shear deformable piezoelectric carbon nanotube/fiber/polymer multiscale laminated composite plates. J Sound Vib 333(14):3236–3251. https://doi.org/10.1016/j.jsv.2014.02.033

    Article  Google Scholar 

  49. He XQ, Rafiee M, Mareishi S, Liew KM (2015) Large amplitude vibration of fractionally damped viscoelastic CNTs/fiber/polymer multiscale composite beams. Compos Struct 131:1111–1123. https://doi.org/10.1016/j.compstruct.2015.06.038

    Article  Google Scholar 

  50. Rafiee M, Nitzsche F, Labrosse M (2016) Rotating nanocomposite thin-walled beams undergoing large deformation. Compos Struct 150:191–199. https://doi.org/10.1016/j.compstruct.2016.05.014

    Article  Google Scholar 

  51. Ebrahimi F, Habibi S (2018) Nonlinear eccentric low-velocity impact response of a polymer-carbon nanotube-fiber multiscale nanocomposite plate resting on elastic foundations in hygrothermal environments. Mech Adv Mater Struct 25(5):425–438. https://doi.org/10.1080/15376494.2017.1285453

    Article  Google Scholar 

  52. Rafiee M, Nitzsche F, Labrosse MR (2018) Modeling and mechanical analysis of multiscale fiber-reinforced graphene composites: Nonlinear bending, thermal post-buckling and large amplitude vibration. Int J Non-Linear Mech 103:104–112. https://doi.org/10.1016/j.ijnonlinmec.2018.05.004

    Article  Google Scholar 

  53. Ebrahimi F, Dabbagh A (2019) Vibration analysis of graphene oxide powder-/carbon fiber-reinforced multi-scale porous nanocomposite beams: a finite-element study. Euro Phys J Plus 134(5):225. https://doi.org/10.1140/epjp/i2019-12594-1

    Article  Google Scholar 

  54. Ebrahimi F, Dabbagh A (2021) An analytical solution for static stability of multi-scale hybrid nanocomposite plates. Eng Comput 37(1):545–559. https://doi.org/10.1007/s00366-019-00840-y

    Article  Google Scholar 

  55. Dabbagh A, Rastgoo A, Ebrahimi F (2020) Post-buckling analysis of imperfect multi-scale hybrid nanocomposite beams rested on a nonlinear stiff substrate. Eng Comput. https://doi.org/10.1007/s00366-020-01064-1

    Article  Google Scholar 

  56. Ebrahimi F, Dabbagh A, Rastgoo A (2020) Static stability analysis of multi-scale hybrid agglomerated nanocomposite shells. Mechanics Based Design of Structures and Machines:1–17. doi: https://doi.org/10.1080/15397734.2020.1848585

  57. Ebrahimi F, Dabbagh A, Rastgoo A, Rabczuk T (2020) Agglomeration effects on static stability analysis of multi-scale hybrid nanocomposite plates. Comput Materials Continua 63(1):41–64. https://doi.org/10.32604/cmc.2020.07947

    Article  Google Scholar 

  58. Ebrahimi F, Dabbagh A (2020) Vibration analysis of multi-scale hybrid nanocomposite shells by considering nanofillers’ aggregation. Waves in Random and Complex Media:1–19. https://doi.org/10.1080/17455030.2020.1810363

  59. Ebrahimi F, Dabbagh A, Rastgoo A (2021) Free vibration analysis of multi-scale hybrid nanocomposite plates with agglomerated nanoparticles. Mech Based Des Struct Mach 49(4):487–510. https://doi.org/10.1080/15397734.2019.1692665

    Article  Google Scholar 

  60. Ebrahimi F, Nopour R, Dabbagh A (2021) Effect of viscoelastic properties of polymer and wavy shape of the CNTs on the vibrational behaviors of CNT/glass fiber/polymer plates. Eng Comput. https://doi.org/10.1007/s00366-021-01387-7

    Article  Google Scholar 

  61. Ferry JD (1980) Viscoelastic Properties of Polymers. 3rd edn. John Wiley & Sons,

  62. Drozdov AD, Kalamkarov AL (1996) A constitutive model for nonlinear viscoelastic behavior of polymers. Polym Eng Sci 36(14):1907–1919. https://doi.org/10.1002/pen.10587

    Article  Google Scholar 

  63. Brinson HF, Brinson LC (2008) Polymer Engineering Science and Viscoelasticity. 1st edn. Springer, Boston, MA, USA. doi: https://doi.org/10.1007/978-0-387-73861-1

  64. Cox HL (1952) The elasticity and strength of paper and other fibrous materials. Br J Appl Phys 3(3):72–79. https://doi.org/10.1088/0508-3443/3/3/302

    Article  Google Scholar 

  65. Aboutalebi R, Eshaghi M, Taghvaeipour A (2021) Nonlinear vibration analysis of circular/annular/sector sandwich panels incorporating magnetorheological fluid operating in the post-yield region. J Intell Mater Syst Struct 32(7):781–796. https://doi.org/10.1177/1045389X20975471

    Article  Google Scholar 

  66. Mobasheri Zafarabadi MM, Aghdam MM (2021) Semi-analytical solutions for buckling and free vibration of composite anisogrid lattice cylindrical panels. Compos Struct 275:114422. https://doi.org/10.1016/j.compstruct.2021.114422

    Article  Google Scholar 

  67. Ebrahimi F, Nopour R, Dabbagh A (2021) Smart laminates with an auxetic ply rested on visco-Pasternak medium: active control of the system’s oscillation. Eng Comput. https://doi.org/10.1007/s00366-021-01533-1

    Article  Google Scholar 

  68. Aboutalebi R, Eshaghi M, Taghvaeipour A, Bakhtiari-Nejad F (2021) Post-Yield characteristics of electrorheological fluids in nonlinear vibration analysis of smart sandwich panels. Mechanics Based Design of Structures and Machines:1–20. doi:https://doi.org/10.1080/15397734.2021.1886946

  69. Al-Furjan MSH, Habibi M, Ni J, Dw J, Tounsi A (2020) Frequency simulation of viscoelastic multi-phase reinforced fully symmetric systems. Eng Comput. https://doi.org/10.1007/s00366-020-01200-x

    Article  Google Scholar 

  70. She G-L (2021) Guided wave propagation of porous functionally graded plates: The effect of thermal loadings. J Therm Stresses 44(10):1289–1305. https://doi.org/10.1080/01495739.2021.1974323

    Article  Google Scholar 

  71. She G-L, Liu H-B, Karami B (2021) Resonance analysis of composite curved microbeams reinforced with graphene nanoplatelets. Thin-Walled Struct 160:107407. https://doi.org/10.1016/j.tws.2020.107407

    Article  Google Scholar 

  72. Ding H-X, She G-L (2021) A higher-order beam model for the snap-buckling analysis of FG pipes conveying fluid. Struct Eng Mech 80(1):63–72. https://doi.org/10.12989/sem.2021.80.1.063

    Article  Google Scholar 

  73. Lu L, She G-L, Guo X (2021) Size-dependent postbuckling analysis of graphene reinforced composite microtubes with geometrical imperfection. Int J Mech Sci 199:106428. https://doi.org/10.1016/j.ijmecsci.2021.106428

    Article  Google Scholar 

  74. Xiao H, Yan K, She G (2021) Study on the characteristics of wave propagation in functionally graded porous square plates. Geomech Eng 26(6):607–615. https://doi.org/10.12989/gae.2021.26.6.607

    Article  Google Scholar 

  75. Ebrahimi F, Dabbagh A (2021) Magnetic field effects on thermally affected propagation of acoustical waves in rotary double-nanobeam systems. Waves Random Complex Media 31(1):25–45. https://doi.org/10.1080/17455030.2018.1558308

    Article  MathSciNet  Google Scholar 

  76. Ebrahimi F, Dabbagh A, Rabczuk T (2021) On wave dispersion characteristics of magnetostrictive sandwich nanoplates in thermal environments. Eur J Mech A Solids 85:104130. https://doi.org/10.1016/j.euromechsol.2020.104130

    Article  MathSciNet  MATH  Google Scholar 

  77. Bich DH, Xuan Nguyen N (2012) Nonlinear vibration of functionally graded circular cylindrical shells based on improved Donnell equations. J Sound Vib 331(25):5488–5501. https://doi.org/10.1016/j.jsv.2012.07.024

    Article  Google Scholar 

  78. Ebrahimi F, Dabbagh A (2020) Mechanics of Nanocomposites: Homogenization and Analysis. 1st edn. CRC Press, Boca Raton, FL, USA. doi: https://doi.org/10.1201/9780429316791

  79. Ebrahimi F, Dabbagh A (2019) Wave Propagation Analysis of Smart Nanostructures. 1st edn. CRC Press, Boca Raton, FL, USA. doi: https://doi.org/10.1201/9780429279225

  80. Ebrahimi F, Hosseini SHS, Bayrami SS (2019) Nonlinear forced vibration of pre-stressed graphene sheets subjected to a mechanical shock: An analytical study. Thin-Walled Structures 141:293–307. https://doi.org/10.1016/j.tws.2019.04.038

    Article  Google Scholar 

  81. Karimiasl M, Ebrahimi F (2019) Large amplitude vibration of viscoelastically damped multiscale composite doubly curved sandwich shell with flexible core and MR layers. Thin-Walled Structures 144:106128. https://doi.org/10.1016/j.tws.2019.04.020

    Article  Google Scholar 

  82. Karimiasl M, Ebrahimi F, Mahesh V (2019) Nonlinear forced vibration of smart multiscale sandwich composite doubly curved porous shell. Thin-Walled Struct 143:106152. https://doi.org/10.1016/j.tws.2019.04.044

    Article  Google Scholar 

  83. Safarpour M, Ghabussi A, Ebrahimi F, Habibi M, Safarpour H (2020) Frequency characteristics of FG-GPLRC viscoelastic thick annular plate with the aid of GDQM. Thin-Walled Structures 150:106683. https://doi.org/10.1016/j.tws.2020.106683

    Article  Google Scholar 

  84. Yarali E, Farajzadeh MA, Noroozi R, Dabbagh A, Khoshgoftar MJ, Mirzaali MJ (2020) Magnetorheological elastomer composites: Modeling and dynamic finite element analysis. Compos Struct 254:112881. https://doi.org/10.1016/j.compstruct.2020.112881

    Article  Google Scholar 

  85. Soleimani H, Goudarzi T, Aghdam MM (2021) Advanced structural modeling of a fold in Origami/Kirigami inspired structures. Thin-Walled Structures 161:107406. https://doi.org/10.1016/j.tws.2020.107406

    Article  Google Scholar 

  86. Kabir H, Aghdam MM (2021) A generalized 2D Bézier-based solution for stress analysis of notched epoxy resin plates reinforced with graphene nanoplatelets. Thin-Walled Structures 169:108484. https://doi.org/10.1016/j.tws.2021.108484

    Article  Google Scholar 

  87. Fallah A, Aghdam MM (2012) Thermo-mechanical buckling and nonlinear free vibration analysis of functionally graded beams on nonlinear elastic foundation. Compos B Eng 43(3):1523–1530. https://doi.org/10.1016/j.compositesb.2011.08.041

    Article  Google Scholar 

  88. Wang Y, Wu D (2017) Free vibration of functionally graded porous cylindrical shell using a sinusoidal shear deformation theory. Aerosp Sci Technol 66:83–91. https://doi.org/10.1016/j.ast.2017.03.003

    Article  Google Scholar 

  89. Wang YQ, Ye C, Zu JW (2019) Nonlinear vibration of metal foam cylindrical shells reinforced with graphene platelets. Aerosp Sci Technol 85:359–370. https://doi.org/10.1016/j.ast.2018.12.022

    Article  Google Scholar 

  90. Bhimaraddi A (1984) A higher order theory for free vibration analysis of circular cylindrical shells. Int J Solids Struct 20(7):623–630. https://doi.org/10.1016/0020-7683(84)90019-2

    Article  MATH  Google Scholar 

  91. Lam KY, Loy CT (1995) Effects of boundary conditions on frequencies of a multi-layered cylindrical shell. J Sound Vib 188(3):363–384. https://doi.org/10.1006/jsvi.1995.0599

    Article  Google Scholar 

  92. Xuebin L (2008) Study on free vibration analysis of circular cylindrical shells using wave propagation. J Sound Vib 311(3):667–682. https://doi.org/10.1016/j.jsv.2007.09.023

    Article  Google Scholar 

  93. Shen H-S (2012) Nonlinear vibration of shear deformable FGM cylindrical shells surrounded by an elastic medium. Compos Struct 94(3):1144–1154. https://doi.org/10.1016/j.compstruct.2011.11.012

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Amirkabir University of Technology, Hafez Ave., 15875-4413, Tehran, Iran

    R. Nopour & M. M. Aghdam

  2. Department of Mechanical Engineering, Faculty of Engineering, Imam Khomeini International University, Noroozian Blvd, 34148-96818, Qazvin, Iran

    F. Ebrahimi

  3. School of Mechanical Engineering, College of Engineering, University of Tehran, North Kargar St, 11155-4563, Tehran, Iran

    A. Dabbagh

Authors
  1. R. Nopour
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. F. Ebrahimi
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. A. Dabbagh
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. M. M. Aghdam
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to F. Ebrahimi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nopour, R., Ebrahimi, F., Dabbagh, A. et al. Nonlinear forced vibrations of three-phase nanocomposite shells considering matrix rheological behavior and nano-fiber waviness. Engineering with Computers 39, 557–574 (2023). https://doi.org/10.1007/s00366-022-01608-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-022-01608-7

Keywords