Skip to main content
SpringerLink
Log in

Integration of a peridynamic fatigue model with two-parameter crack driving force

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

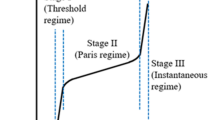
Abstract

In this study, a new crack growth prediction modeling approach based on an ordinary state-based peridynamic formulation is developed to improve predictive modeling of R-ratio effects on fatigue crack growth behavior. The proposed modeling method integrates the recently developed analytical remaining-life solution of the peridynamic fatigue model and a generalized two-parameter crack driving force model to predict crack growth rates at various R-ratios. The two-parameter driving force model is formulated to combine two independent crack growth driving force parameters of \({K}_{\mathrm{max}}\) and \(\Delta K\) to incorporate R-ratio effects on crack growth behavior. Predicted crack growth rates are validated with crack growth data at various R-ratio effects for 2024-T3 and 7075-T6 aluminum alloys. Results show that very good agreements between experimental data and model predictions at four different R-ratios for both aluminum alloys. The proposed modeling approach shows efficient and accurate computations of crack growth rates by accounting different R-ratio loading conditions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Gerber W (1874) Bestimmung der zulossigenin eisen construcionen. Z Bayer Arch Ing 1874:101–110

    Google Scholar 

  2. Goodman J (1930) Mechanics applied to engineering, vol 1, 9th ed. Longmans Green and Co., London

    Google Scholar 

  3. CR Soderberg (1930) ASME Trans ;52(APM-52–2), pp 13–28

  4. Ince A, Glinka G (2011) A modification of Morrow and Smith-Watson-Topper mean stress correction models. Fatigue Fract Eng Mater Struct 34:854–867. https://doi.org/10.1111/j.1460-2695.2011.01577.x

    Article  Google Scholar 

  5. Ince A, Glinka G (2014) A generalized damage parameter for multiaxial fatigue life prediction under proportional and non-proportional loadings. Int J Fatigue 62:34–41. https://doi.org/10.1016/j.ijfatigue.2013.10.007

    Article  Google Scholar 

  6. Correia J, Raposo P, Muniz-Calvente M (2017) A generalization of the fatigue Kohout-Věchet model for several fatigue damage parameters. Eng Fract Mech 185:284–300

    Google Scholar 

  7. Zhu SP, Lei Q, Wang QY (2017) Mean stress and ratcheting corrections in fatigue life prediction of metals. Fatigue Fract Eng Mater Struct 40:1343–1354

    Google Scholar 

  8. Ince A (2017) A mean stress correction model for tensile and compressive mean stress fatigue loadings. Fatigue Fract Eng Mater Struct 40:939–948. https://doi.org/10.1111/ffe.12553

    Article  Google Scholar 

  9. Ince A (2017) A generalized mean stress correction model based on distortional strain energy. Int J Fatigue 104:273–282. https://doi.org/10.1016/j.ijfatigue.2017.07.023

    Article  Google Scholar 

  10. Paris PC, Erdogan F (1963) A critical analysis of crack propagation laws. J Basic Eng 18:528–534. https://doi.org/10.1115/1.3656900

    Article  Google Scholar 

  11. Paris PC, Tada H, Donald JK (1999) Service load fatigue damage—a historical perspective. Int J Fatigue 21:35–46

    Google Scholar 

  12. K. Walker (1970) The effect of stress ratio during crack propagation and fatigue for 2024-T3 and 7075-T6 aluminum. In: Effects of environment and complete loading history on fatigue life. ASTM STP 462. Philadelphia, PA: American Society for Testing and Materials, pp 1–14

  13. Erdogan F (1967) Crack propagation theories. NASA CR-901

  14. McEvily AJ, Groeger J (1978) On the threshold for fatigue crack growth. Adv Res Strength Fract Mater 1978:1293–1298. https://doi.org/10.1016/b978-0-08-022140-3.50087-2

    Article  Google Scholar 

  15. Forman RG, Mettu SR (1992) Behavior of surface and corner cracks subjected to tensile and bending loads in Ti-6Al-4V alloy. In: Fracture mechanics: 22nd symposium, vol 1, pp 519–546

  16. Dinda S, Kujawski D (2004) Correlation and prediction of fatigue crack growth for different R-ratios using and parameters. Eng Fract Mech 71:1779–1790

    Google Scholar 

  17. Noroozi AH, Glinka G, Lambert S (2007) A study of the stress ratio effects on fatigue crack growth using the unified two-parameter fatigue crack growth driving force. Int J Fatigue 29:1616–1633

    MATH  Google Scholar 

  18. Bang DJ, Ince A, Tang L (2018) A modification of UniGrow 2-parameter driving force model for short fatigue crack growth. Fatigue Fract Eng Mater Struct 42:45–60. https://doi.org/10.1111/ffe.12865

    Article  Google Scholar 

  19. Bang DJ, Ince A, Noban M (2019) Modeling approach for a unified crack growth model in short and long fatigue crack regimes. Int J Fatigue 128:105182

    Google Scholar 

  20. Bang DJ, Ince A (2020) A short and long crack growth model based on 2-parameter driving force and crack growth thresholds. Int J Fatigue 141:105870

    Google Scholar 

  21. Dugdale DS (1960) Yielding of steel sheets containing slits. J Mech Phys Solids 8:100–104

    Google Scholar 

  22. Barenblatt GI (1962) The mathematical theory of equilibrium cracks in brittle fracture. Adv Appl Mech 7:56–125

    Google Scholar 

  23. Hillerborg A, Modeer M, Petersson PE (1976) Analysis of crack formation and crack growth by means of fracture mechanics and finite elements. Cem Concr Res 6:773–781

    Google Scholar 

  24. Xu XP, Needleman A (1994) Numerical simulations of fast crack growth in brittle solids. J Mech Phys Solids 42:1397–1434

    MATH  Google Scholar 

  25. Proudhon H, Li J, Wang F, Roos A, Chiaruttini V, Forest S (2016) 3D simulation of short fatigue crack propagation by finite element crystal plasticity and remeshing. Int J Fatigue 82:238–246

    Google Scholar 

  26. Trädegård A, Nilsson F, Östlund S (1998) Fem-remeshing technique applied to crack growth problems. Comput Methods Appl Mech Eng 160:115–131

    MATH  Google Scholar 

  27. Bouchard PO, Bay F, Chastel Y (2003) Numerical modelling of crack propagation: automatic remeshing and comparison of different criteria. Comput Methods Appl Mech Eng 192:3887–3908

    MATH  Google Scholar 

  28. de Jesus AMP, da Silva ALL, Figueiredo MV, Correia JAFO, Ribeiro AS, Fernandes AA (2011) Strain-life and crack propagation fatigue data from several Portuguese old metallic riveted bridges. Eng Fail Anal 18:148–163

    Google Scholar 

  29. Rao BN, Rahman S (2000) An efficient meshless method for fracture analysis of cracks. Comput Mech 26:398–408

    MATH  Google Scholar 

  30. Duflow M, Hung ND (2004) Fatigue crack growth analysis by an enriched meshless method. J Comput Appl Math 168:155–164

    MathSciNet  MATH  Google Scholar 

  31. Marc D, Hung ND (2004) A meshless method with enriched weight functions for fatigue crack growth. Int J Numer Meth Eng 59:1945–1961

    MATH  Google Scholar 

  32. Li SC, Li SC, Cheng YM (2005) Enriched meshless manifold method for two-dimensional crack modeling. Theor Appl Fract Mech 44:234–248

    Google Scholar 

  33. Barbieri E, Petrinic N, Meo M, Tagarielli VL (2012) A new weight-function enrichment in meshless methods for multiple cracks in linear elasticity. Int J Numer Meth Eng 90:177–195

    MathSciNet  MATH  Google Scholar 

  34. Belytschko T, Black T (1999) Elastic crack growth in finite elements with minimal remeshing. Int J Numer Meth Eng 45:601–620

    MATH  Google Scholar 

  35. Moes N, Dolbow J, Belytschko T (1999) A finite element method for crack growth without remeshing. Int J Numer Meth Eng 46:131–150

    MathSciNet  MATH  Google Scholar 

  36. Shi J, Chopp D, Lua J, Sukumar N, Belytschko T (2010) Abaqus implementation of extended finite element method using a level set representation for three-dimensional fatigue crack growth and life predictions. Eng Fract Mech 77:2840–2863

    Google Scholar 

  37. Sukumar N, Chopp DL, Moran B (2003) Extended finite element method and fast marching method for three-dimensional fatigue crack propagation. Eng Fract Mech 70:29–48

    Google Scholar 

  38. Chin EB, Lasserre JB, Sukumar N (2017) Modeling crack discontinuities without element-partitioning in the extended finite element method. Int J Numer Methods Eng 110:1021–1048

    MathSciNet  Google Scholar 

  39. Silling SA (2000) Reformulation of elasticity theory for discontinuities and long-range forces. J Mech Phys Solids 48:175–209

    MathSciNet  MATH  Google Scholar 

  40. Silling SA, Epton M, Weckner O, Xu J, Askari A (2007) Peridynamics states and constitutive modeling. J Elast 88:151–184

    MathSciNet  MATH  Google Scholar 

  41. Silling SA, Lehoucq RB (2010) Peridynamic theory of solid mechanics. Sandia National Labs Technical report. Adv Appl Mech 44:73–168

    Google Scholar 

  42. Silling SA, Askari E (2005) A meshfree method based on the peridynamic model of solid mechanics. Comput Struct 83:1526–1535

    Google Scholar 

  43. Silling SA, Lehoucq RB (2008) Convergence of peridynamics to classical elasticity theory. J Elast 93:13–37

    MathSciNet  MATH  Google Scholar 

  44. John A, Mitchell A (2011) Nonlocal, ordinary, state-based plasticity model for peridynamics, Sandia Report SAND2011-3166. Sandia National Laboratories, Albuquerque

  45. Madenci E, Oterkus S (2016) Ordinary state-based peridynamics for plastic deformation according to von Mises yield criteria with isotropic hardening. J Mech Phys Solids 86:192–219

    MathSciNet  Google Scholar 

  46. Mitchell JA (2011) A non-local, ordinary-state-based viscoelasticity model for peridynamics. Sandia National Lab, Report 8064, pp 1–28

  47. Weckner O, Abdullah N, Mohamed N (2013) Viscoelastic material models in peridynamics. Appl Math Comput 219:6039–6043

    MathSciNet  MATH  Google Scholar 

  48. Foster JT, Silling SA, Chen WW (2010) Viscoplasticity using peridynamics. Int J Numer Methods Eng 81:1242–1258

    MATH  Google Scholar 

  49. Silling SA, Bobaru F (2005) Peridynamic modeling of membranes and fibers. Int J Nonlin Mech 40:395–409

    MATH  Google Scholar 

  50. Bang DJ, Madenci E (2017) Peridynamic Modeling of Hyperelastic Membrane Deformation. J Eng MateR-T ASME 139:10

    Google Scholar 

  51. Kilic B, Agwai A, Madenci E (2009) Peridynamic theory for progressive damage prediction in centeR-cracked composite laminates. Compos Struct 90:141–151

    Google Scholar 

  52. Oterkus E, Madenci E (2012) Peridynamic analysis of fiber-reinforced composite materials. Mech Adv Mater Struc 7:45–84

    Google Scholar 

  53. Wenke Hu, Ha YD, Bobaru F (2012) Peridynamic model for dynamic fracture in unidirectional fiber-reinforced composites. Comput Methods Appl Mech Engrg 217–220:247–261

    MathSciNet  MATH  Google Scholar 

  54. Rokkam S, Gunzburger M, Brothers M, Phan N, Goel K (2019) A nonlocal peridynamics modeling approach for corrosion damage and crack propagation. Theor Appl Fract Mec 101:373–387

    Google Scholar 

  55. Meo DD, Oterkus E (2017) Finite element implementation of a peridynamic pitting corrosion damage model. Ocean Eng 135:76–83

    Google Scholar 

  56. Tan Y, Liu Q, Zhang L, Liu L, Lai X (2020) Peridynamics model with surface correction near insulated cracks for transient heat conduction in functionally graded materials. Mater. https://doi.org/10.3390/ma13061340

    Article  Google Scholar 

  57. Wanga L, Xub J, Wanga J (2018) A peridynamic framework and simulation of non-Fourier and nonlocal heat conduction. Int J Heat Mass Transf 118:1284–1292

    Google Scholar 

  58. Diyaroglu C, Oterkus S, Oterkus E, Madenci E (2017) Peridynamic modeling of diffusion by using finite-element analysis. IEEE Trans Compon Pack Manuf Technol 7:1823–1831

    Google Scholar 

  59. Chen Z, Bobaru F (2015) Selecting the kernel in a peridynamic formulation: A study for transient heat diffusion. Comput Phys Commun 197:51–60

    Google Scholar 

  60. Ren H, Zhuang X, Cai Y, Rabczuk T (2016) Dual-horizon peridynamics. Int J Numer Meth Eng 108:1451–1476

    MathSciNet  Google Scholar 

  61. Rabczuk T, Ren H (2017) A peridynamics formulation for quasi-static fracture and contact in rock. Eng Geol 225:42–48

    Google Scholar 

  62. Ren H, Zhuang X, Rabczuk T (2017) Dual-horizon peridynamics: a stable solution to varying horizons. Comput Methods Appl Mech Eng 318:762–782

    MathSciNet  MATH  Google Scholar 

  63. Rabczuk T, Ren H, Zhuang X (2019) A nonlocal operator method for partial differential equations with application to electromagnetic waveguide problem. CMC 59:31–55

    Google Scholar 

  64. Ren H, Zhuang X, Rabczuk T (2020) A higher order nonlocal operator method for solving partial differential equations. Comput Methods Appl Mech Eng 367:113–132

    MathSciNet  MATH  Google Scholar 

  65. Ren H, Zhuang X, Oterkus E, Zhu H, Rabczuk T (2021) Nonlocal strong forms of thin plate, gradient elasticity, magneto-electro-elasticity and phase-field fracture by nonlocal operator method. Eng Comput. https://doi.org/10.1007/s00366-021-01502-8

    Article  Google Scholar 

  66. Madenci E, Dorduncu M, Barut A, Phan N (2018) A state-based peridynamic analysis in a finite element framework. Eng Fract Mech 195:104–128

    Google Scholar 

  67. Madenci E, Dorduncu M, Barut A, Phan N (2018) Weak form of peridynamics for nonlocal essential and natural boundary conditions. Comput Methods Appl Mech Eng 337:598–631

    MathSciNet  MATH  Google Scholar 

  68. Madenci E, Dorduncu M, Gu X (2019) Peridynamic least squares minimization. Comput Methods Appl Mech Eng 348:846–874

    MathSciNet  MATH  Google Scholar 

  69. Madenci E, Barut A, Dorduncu M (2019) Peridynamic differential operator for numerical analysis, Springer Nature, Switzerland

  70. Oterkus E, Guven I, Madenci E (2010) Fatigue failure model with peridynamic theory, In IEEE Intersociety conference on thermal and thermomechanical phenomena in electronic systems (ITherm), Las Vegas, NV, pp 1–6

  71. Silling SA, Askari A (2014) Peridynamic model for fatigue cracking Tech. rep. no. SAND2014-18590. Albuquerque (NM, United States): Sandia National Laboratories (SNL-NM)

  72. Wang F, Ma Y, Guo Y, Huang W (2019) Studies on quasi-static and fatigue crack propagation behaviours in friction stir welded joints using peridynamic theory. Adv Mater Sci Eng 3:1–16

    Google Scholar 

  73. Liu Y, Deng L, Zhong W, Xu J, Xiong W (2020) A new fatigue reliability analysis method for steel bridges based on peridynamic theory. Eng Fract Mech 236:107214

    Google Scholar 

  74. Zhu N, Kochan C, Oterkus E, Oterkus S (2021) Fatigue analysis of polycrystalline materials using Peridynamic Theory with a novel crack tip detection algorithm. Ocean Eng 222:108572

    Google Scholar 

  75. Bang DJ, Ince A, Oterkus E, Oterkus S (2021) Crack growth modeling and simulation of a peridynamic fatigue model based on numerical and analytical solution approaches. Theor Appl Fract Mech 114:103026

    Google Scholar 

  76. Madenci E, Barut A, Yaghoobi A, Phan N, Fertig RS (2021) Combined peridynamics and kinetic theory of fracture for fatigue failure of composites under contant and variable amplitude loading. Theor Appl Fract Mech 112:102824

    Google Scholar 

  77. Zhang Y, Madenci E (2021) A coupled peridynamic and finite element approach in ANSYS framework for fatigue life prediction based on the kinetic theory of fracture. J Peridyn Nonlocal Model. https://doi.org/10.1007/s42102-021-00055-0

    Article  Google Scholar 

  78. Nguyen CT, Oterkus S, Oterkus E (2021) Implementation of modified Wheeler model in peridynamic fatigue model to predict effects of overload and underl. Theor Appl Fract Mech 116:103115

    Google Scholar 

  79. Nguyen CT, Oterkus S, Oterkus E (2021) An energy-based peridynamic model for fatigue cracking. Eng Fract Mech 241:107373

    Google Scholar 

  80. Madenci E, Oterkus E (2014) Peridynamic theory and its applications. Springer, New York

    MATH  Google Scholar 

  81. Kilic B, Madenci E (2010) An adaptive dynamic relaxation method for quasi-static simulations using the peridynamic theory. Theor Appl Fract Mech 53:194–201

    Google Scholar 

  82. Hudson CM (1969) Effect of stress ratio on fatigue-crack growth in 7075-T6 and 2024-T3 Aluminum-Alloy Specimens, NASA TN D-5390, 1969

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical, Industrial and Aerospace Engineering, Concordia University, Montreal, Canada

    D. J. Bang & A. Ince

Authors
  1. D. J. Bang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Ince
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Ince.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bang, D.J., Ince, A. Integration of a peridynamic fatigue model with two-parameter crack driving force. Engineering with Computers 38, 2859–2877 (2022). https://doi.org/10.1007/s00366-022-01619-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-022-01619-4

Keywords

Search

Navigation