On the size-dependent bending and buckling of the partially covered laminated microplate

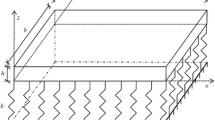
Abstract

The bending and buckling of the microcomponents show size dependency. The strain gradient elasticity theory is proposed to explain the size dependency. In this paper, we derive the theoretical relations among the modified strain gradient elasticity theory, the modified couple stress theory and the general strain gradient elasticity theory, and clarify the degradation relation. The general theory includes all strain gradients while the modified strain gradient elasticity theory and the modified couple stress theory only contain part of strain gradients. By ignoring the deviatoric part of the strain gradients $\eta _{ijk}^{'(2)}$ or the symmetric part of the strain gradients $\eta _{ijk}^{s}$, the general theory is simplified as the modified couple stress theory or the modified strain gradient elasticity theory, respectively. The ability of the general theory and the reduced theories in describing the bending and buckling response of the partially covered laminated microplate is subsequently compared. Results reveal that the general theory predicts smaller bending deflection and axial displacement while larger buckling load than that of the reduced theories. The general theory is more effective in reflecting the size effects. In addition, it is found that the increase of the thickness or radius of the upper elastic layer makes the buckling load increase while the deflection increase firstly and then decrease. There exists the specific radius ratio and thickness ratio to make the clamped-clamped microplate achieve the maximum deflection.

Graphical abstract

Appendix A

The matrix $\left[ M(P) \right]$ in Eq. (74) is derived as

$$\begin{aligned} \left[ M(P) \right] = \left[ \begin{array}{ccccccccccc} 1 &{}R^2 &{}m_{1} &{}m_{2} &{} m_{3} &{} m_{4} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} m_{5} &{} m_{6} &{} m_{7} &{} m_{8} &{} m_{9} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} m_{10} &{} m_{11} &{} m_{12} &{} m_{13} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ m_{14} &{} m_{15} &{} m_{16} &{} m_{17} &{}m_{18} &{} m_{19} &{} -1 &{} m_{20} &{} m_{21} &{} m_{22} &{} 0 \\ 0 &{} m_{23} &{} m_{24} &{} m_{25} &{} m_{26} &{} m_{27} &{} 0 &{} m_{28} &{} m_{29} &{} m_{30} &{} 0\\ 0 &{} m_{31} &{} m_{32} &{} m_{33} &{} m_{34} &{} m_{35} &{} 0 &{} -2 &{} m_{36} &{} m_{37} &{} 0\\ 0 &{} 0 &{} 0 &{} m_{38} &{} m_{39} &{} m_{40} &{} 0 &{} 0 &{} m_{41} &{} m_{42} &{} 0 \\ 0 &{} m_{43} &{} m_{44} &{} m_{45} &{} m_{46} &{} m_{47} &{} 0 &{} m_{48} &{} m_{49} &{} m_{50} &{} m_{51} \\ 0 &{} 0 &{} m_{52} &{} m_{53} &{} m_{54} &{} m_{55} &{} 0 &{} 0 &{} m_{56} &{} m_{57} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} m_{58} &{} m_{59} &{} m_{60} &{} m_{61} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} m_{62} &{} m_{63}&{} 0 \\ \end{array} \right] \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} m_{1}&=lnR \quad m_{2}=R^2lnR \\ m_{3}&=I_{0}(dR) \quad m_{4}=k_{0}(dR)\\ m_{5}&=-2 c_{3(1)} I_{1} + 2g_{7(1)} h_{2}+4 A_{2(1)} h_{2}\\ m_{6}&=(-2A_{1(1)} +2A_{7(1)} )/R^4\\&\quad +(-c_{3(1)}I_{1}+g_{7(1)}h_{1}-2g_{2(1)}h_{1})/R^2\\ m_{7}&=(6A_{1(1)}-2A_{7(1)})/R^2-c_{3(1)}I_{1}(2lnR+1)\\&\quad +g_{7(1)}h_{1}(2lnR+1)+4A_{2(1)}(lnR+1)\\&\quad +2g_{2(1)}h_{1}(2lnR+3)\\ m_{8}&=-\frac{1}{4}d^4 A_{1(1)}+\frac{3}{2}I_{0}(dR) +2I_{2}(dR) \\&\quad +\frac{1}{2}I_{4}(dR) -\frac{A_{1(1)}d^3}{4R}(I_{3}(dR) +3I_{1}(dR))\\&\quad +\left( \frac{1.5A_{1(1)}d^2}{R^2} -\frac{ 0.5 A_{7(1)} d^2}{R^2}+0.5 A_{2(1)} d^2+g_{2(1)}h_{1} d^2\right) \\&\quad (I_{0}(dR)+I_{2}(dR)) \\&\quad +\left( -\frac{3A_{1(1)}d}{R^3}+\frac{A_{7(1)}d}{R^3}-\frac{c_{3(1)}I_{1}d}{R}\right. \\&\quad \left. +\frac{ g_{7(1)}h_{1}d}{R}+\frac{dA_{2(1)}}{R} \right) I_{1}(dR)\\ m_{9}&=-\frac{d^4A_{1(1)}}{4} \left( \frac{3}{2}k_{0}(dR) +2k_{2}(dR) + \frac{1}{2}k_{4}(dR) \right) \\&\quad + \frac{A_{1(1)}d^3}{4R} (3k_{1}(dR) +k_{3}(dR) )\\&\quad +\left( \frac{1.5A_{1(1)} d^2}{R^2}-\frac{0.5 A_{7(1)} d^2}{R^2} +0.5A_{2(1)} d^2 \right. \\&\quad \left. +g_{2(1)} h_{1} d^2\right) (k_{0}(dR)+k_{2}(dR))\\&\quad \left( \frac{3 A_{1(1)}d}{R^3}-\frac{A_{7(1)} d}{R^3} + \frac{c_{3(1)} I_{(1)} d}{R} \right. \\&\quad \left. -\frac{g_{7(1)} h_{(1)} d}{R} -\frac{d A_{2(1)} }{R} \right) k_{1}(dR) \end{aligned} \end{aligned}$$

(100)

$$\begin{aligned} \begin{aligned} m_{10}&=\frac{2A_{1(1)}-2A_{7(1)}}{R^3} \\ m_{11}&=\frac{2A_{1(1)}+2A_{7(1)}}{R}\\ m_{12}&=\frac{A_{1(1)} d^3}{4} (3I_{1}(dR)+I_{3}(dR))\\&\quad + \frac{A_{7(1)} d^2}{2R} (I_{0}(dR)+I_{2}(dR))\\&\quad +\frac{-A_{7(1)} d}{R^2} I_{1}(dR)\\ m_{13}&=\frac{A_{1(1)} d^3}{4} (-3k_{1}(dR)-k_{3}(dR))\\&\quad + \frac{A_{7(1)} d^2}{2R} (k_{0}(dR)+k_{2}(dR)) +\frac{A_{7(1)} d}{R^2} k_{1}(dR)\\ m_{14}&=1 \quad m_{15}=R_{1}^2 \quad m_{16}=lnR_{1} \\ m_{17}&=R_{1}^2 lnR_{1} \quad m_{18}=I_{0}(dR_{1}) \quad m_{19}=k_{0}(dR_{1})\\ m_{20}&=-R_{1}^2 \quad m_{21}=-J_{0}(\sqrt{s_{1}}R_{1})\\ m_{22}&=-J_{0}(\sqrt{s_{2}}R_{1}) \quad m_{23}=2R_{1} \quad m_{24}=\frac{1}{R_{1} }\\ m_{25}&=2R_{1}lnR_{1}+R_{1} \quad m_{26}=dI_{1}(dR_{1}) \\ m_{27}&=-dk_{1}(dR_{1}) \quad m_{28}=-2R_{1}\\ m_{29}&=\sqrt{s_{1}} J_{1}(\sqrt{s_{1}}R_{1}) \\ m_{30}&=\sqrt{s_{2}} J_{1}(\sqrt{s_{2}}R_{1}) \quad m_{31}=2 \quad m_{32}=-\frac{1}{R_{1}^2}\\ m_{33}&=2lnR_{1}+3 \quad m_{34}=\frac{d^2}{2}(I_{0}(dR_{1})+I_{2}(dR_{1}) )\\ m_{35}&=\frac{d^2}{2}(k_{0}(dR_{1})+k_{2}(dR_{1}) )\\ m_{36}&=\frac{s_{1}}{2} J_{0}(\sqrt{s_{1}}R_{1})-J_{2}(\sqrt{s_{1}}R_{1})\\ m_{37}&=\frac{s_{2}}{2} J_{0}(\sqrt{s_{2}}R_{1})-J_{2}(\sqrt{s_{2}}R_{1})\\ m_{38}&= \frac{4A_{2(1)}}{R_{1}} \\ m_{39}&=\frac{d^5A_{1(1)}}{4} (\frac{5}{2} I_{1}(dR_{1})+\frac{5}{4} I_{3}(dR_{1})+\frac{1}{4} I_{5}(dR_{1}))\\&\quad +\left( \frac{-3A_{1(1)}}{R_{1}^{4}} + \frac{d A_{2(1)}}{R_{1}^2} \right) I_{1}(dR_{1})\\&\quad +\left( \frac{3A_{1(1)}d^2}{2R_{1}^{3}}-\frac{ A_{2(1)}d^2}{2R_{1}}\right) (I_{0}(dR_{1})+I_{2}(dR_{1}) )\\&\quad +\left( \frac{-3A_{1(1)}d^3}{4R_{1}^{2}} + \frac{-A_{2(1)}d^3}{4} \right) ( 3 I_{1}(dR_{1}) +I_{3}(dR_{1}) )\\&\quad \frac{A_{1(1)}d^4}{2R_{1}} \left( \frac{3}{2}I_{0}(dR_{1}) + 2I_{2}(dR_{1})+\frac{1}{2}I_{4}(dR_{1}) \right) \\ m_{40}&=\frac{A_{1(1)}d^5}{4} (-\frac{5}{2}k_{1}(dR_{1})-\frac{5}{4}k_{3}(dR_{1})\\&\quad -\frac{1}{4}k_{5}(dR_{1}) +\left( \frac{3A_{1(1)}d}{R_{1}^4}-\frac{A_{2(1)}d}{R_{1}^2} \right) \\&\quad k_{1}(dR_{1}) +\left( \frac{3A_{1(1)}d^2}{2R_{1}^3}-\frac{A_{2(1)}d^2}{2R_{1}}\right) \\&\quad ( k_{0}(dR_{1}) +k_{2}(dR_{1}) ) +\left( \frac{3A_{1(1)}d^3}{4R_{1}^2}+\frac{A_{2(1)}d^3}{4}\right) \\&\quad ( 3k_{1}(dR_{1}) +k_{3}(dR_{1}) ) +\frac{A_{1(1)}d^4}{2R_{1}}\\&\quad \left( \frac{3}{2}k_{0}(dR_{1}) +2k_{2}(dR_{1})+\frac{1}{2}k_{4}(dR_{1})\right) \end{aligned} \end{aligned}$$

(101)

$$\begin{aligned} \begin{aligned} m_{41}&=-0.5(A_{3}s_{1}^{2.5}m-A_{1}s_{1}^{2.5}) \left( \frac{5}{4}J_{1}(\sqrt{s_{1}}R_{1})\right. \\&\quad \left. -\frac{5}{8}J_{3}(\sqrt{s_{1}}R_{1})+\frac{1}{8}J_{5}(\sqrt{s_{1}}R_{1})\right) \\&\quad -\left( \frac{3A_{1} \sqrt{s_{1}}}{R_{1}^4} -\frac{3A_{3}\sqrt{s_{1}}m}{R_{1}^4} -\frac{A_{2}\sqrt{s_{1}}}{R_{1}^2} +\frac{A_{4}\sqrt{s_{1}}m}{R_{1}^2} \right) \\&\quad J_{1}(\sqrt{s_{1}}R_{1}) -\left( \frac{-3A_{1}s_{1}}{2R_{1}^3} +\frac{3A_{3}s_{1}m}{2R_{1}^3} + \frac{A_{2}s_{1}}{2R_{1}} -\frac{A_{4}s_{1}m}{2R_{1}} \right) \\&\quad (J_{0}(\sqrt{s_{1}}R_{1})-J_{2}(\sqrt{s_{1}}R_{1})) \\&\quad -\left( \frac{3A_{1}s_{1}^{0.5}}{2R_{1}^2} -\frac{3A_{3}s_{1}^{1.5}m}{2R_{1}^2} + \frac{A_{2}s_{1}^{1.5}}{2} -\frac{A_{4}s_{1}^{1.5}m}{2} \right) \\&\quad (-1.5J_{1}(\sqrt{s_{1}}R_{1})+0.5J_{3}(\sqrt{s_{1}}R_{1}))\\&\quad -\left( -\frac{A_{1}s_{1}^{2}m}{R1}+\frac{A_{3}s_{1}^{2}m}{R1} \right) \\&\quad \left( -\frac{3}{4} J_{0}(\sqrt{s_{1}}R_{1})+J_{2}(\sqrt{s_{1}}R_{1}) - \frac{1}{4} J_{4}(\sqrt{s_{1}}R_{1})\right) \end{aligned} \end{aligned}$$

(102)

$$\begin{aligned} \begin{aligned} m_{42}&= -(-0.5(A_{1}s_{2}^{2.5}m+A_{3}s_{2}^{2.5}n)\\&\quad \left( \frac{5}{4}J_{1}(\sqrt{s_{2}}R_{1}) -\frac{5}{8}J_{3}(\sqrt{s_{2}}R_{1}) +\frac{1}{8}J_{5}(\sqrt{s_{2}}R_{1})\right) \\&\quad - \left( \frac{3A_{1} \sqrt{s_{2}}}{R_{1}^4} -\frac{3A_{3} \sqrt{s_{2}}n}{R_{1}^4} -\frac{A_{2} \sqrt{s_{2}}n}{R_{1}^2} +\frac{A_{4} \sqrt{s_{2}}n}{R_{1}^2} \right) \\&\quad J_{1}(\sqrt{s_{2}}R_{1}) - \left( \frac{-3A_{1}s_{2}}{2R_{1}^3} +\frac{3A_{3}s_{2}n}{2R_{1}^3} + \frac{A_{2}s_{2}}{2R_{1}} -\frac{A_{4}s_{2}n}{2R_{1}} \right) \\&\quad (J_{0}(\sqrt{s_{2}}R_{1})-J_{2}(\sqrt{s_{2}}R_{1})) \\&\quad - \left( \frac{3A_{1}s_{2}^{1.5}}{2R_{1}^2} -\frac{3A_{3}s_{2}^{1.5}n}{2R_{1}^2} + \frac{A_{2}s_{2}^{1.5}}{2} -\frac{A_{4}s_{2}^{1.5}n}{2} \right) \\&\quad (1.5J_{1}(\sqrt{s_{2}}R_{1})+0.5J_{3}(\sqrt{s_{2}}R_{1}))\\&\quad - \left( -\frac{A_{1}s_{2}^{2}}{R_{1}}+\frac{A_{3}s_{2}^{2}n}{R_{1}} \right) \\&\quad \left( -\frac{3}{4} J_{0}(\sqrt{s_{2}}R_{1})+J_{2}(\sqrt{s_{2}}R_{1}) - \frac{1}{4} J_{4}(\sqrt{s_{2}}R_{1})\right) \end{aligned} \end{aligned}$$

(103)

$$\begin{aligned} \begin{aligned} m_{43}&=-2c_{3(1)}I_{(1)}+2g_{7(1)}h_{(1)}+4A_{2(1)}+4g_{2(1)}h_{(1)}\\ m_{44}&=\frac{-2A_{1(1)}+2A_{7(1)}}{R_{1}^4}\\&\quad +\frac{-c_{3(1)}I_{(1)}+g_{7(1)}h_{(1)}-2g_{2(1)}h_{(1)}}{R_{1}^2}\\ m_{45}&=\frac{6A_{1(1)}-2A_{7(1)}}{R_{1}^2} -c_{3(1)}I_{(1)}(2ln(R_{1})+1)\\&\quad +g_{7(1)}h_{(1)}(2ln(R_{1})+1)\\&\quad +4A_{2(1)}(2ln(R_{1})+1) +2g_{2(1)}h_{(1)}(2ln(R_{1})+3) \end{aligned} \end{aligned}$$

(104)

$$\begin{aligned} \begin{aligned} m_{46}&=\frac{-d^4A_{1(1)}}{4} \left( \frac{3}{2} I_{0}(dR_{1}) +2 I_{2}(dR_{1}\right) \\&\quad +\frac{1}{2} I_{4}(dR_{1}) ) +\frac{d^3A_{1(1)}}{4R_{1}} ( 3I_{1}(dR_{1}) +I_{3}(dR_{1}) ) \\&\quad +\left( \frac{1.5A_{1(1)}d^2}{R_{1}^2} -\frac{0.5A_{7(1)}d^2}{R_{1}^2} +0.5A_{2(1)}d^2 +g_{2(1)}h_{1}d^2 \right) \\&\quad ( I_{0}(dR_{1})+I_{2}(dR_{1} ) \\&\quad +\left( -\frac{3A_{1(1)}d}{R_{1}^3} +\frac{A_{7(1)}d}{R_{1}^3} -\frac{c_{3(1)}I_{(1)}d}{R_{1}}\right. \\&\quad \left. +\frac{g_{7(1)}h_{(1)}d}{R_{1}} +\frac{A_{2(1)}d}{R_{1}} \right) I_{1}(dR_{1}) \end{aligned} \end{aligned}$$

(105)

$$\begin{aligned} \begin{aligned} m_{47}&=\frac{-d^4A_{1(1)}}{4} \left( \frac{3}{2} k_{0}(dR_{1}) +2 k_{2}(dR_{1}) +\frac{1}{2} k_{4}(dR_{1}) \right) \\&\quad +\frac{d^3A_{1(1)}}{4R_{1}} ( 3k_{1}(dR_{1}) +k_{3}(dR_{1}) ) \\&\quad +\left( \frac{1.5A_{1(1)}d^2}{R_{1}^2} -\frac{0.5A_{7(1)}d^2}{R_{1}^2} +0.5A_{2(1)}d^2 +g_{2(1)}h_{1}d^2 \right) \\&\quad ( k_{0}(dR_{1})+k_{2}(dR_{1} ) \\&\quad +\left( -\frac{3A_{1(1)}d}{R_{1}^3} -\frac{A_{7(1)}d}{R_{1}^3} +\frac{c_{3(1)}I_{1}d}{R_{1}} -\frac{g_{7(1)}h_{(1)}d}{R_{1}} -\frac{A_{2(1)}d}{R_{1}} \right) k_{1}(dR_{1}) \end{aligned} \end{aligned}$$

(106)

$$\begin{aligned} \begin{aligned} m_{48}&= 2(c_{3(1)}I_{(1)}+c_{3(2)}I_{(2)}) -2(g_{7(1)}h_{(1)}+g_{7(2)}h_{(2)}) \\&\quad -4(g_{2(1)}h_{(1)} +g_{2(2)}h_{(2)}) -4A_{2}\\ m_{49}&= -\frac{A1 s_{1}^2 m}{2} \left( -\frac{3}{4}J_{0}(\sqrt{s_{1}}R_{1}) +J_{2}(\sqrt{s_{1}}R_{1}) -\frac{1}{4}J_{4}(\sqrt{s_{1}}R_{1})\right) \\&\quad - \frac{A_{(1)} s_{1}^{1.5} -A_{(1)} s_{1}^{1.5} m }{2R_{1}} \left( -\frac{3}{2} J_{1}(\sqrt{s_{1}} R_{1}) +\frac{1}{2} J_{3}(\sqrt{s_{1}} R_{1}) \right) \\&\quad - \left( \frac{-3A_{(1)} s_{1} +3A_{(3)} s_{1} m }{2R_{1}^{2}} +\frac{A_{(7)} s_{1} -A_{(8)} s_{1} m }{2R_{1}^{2}}\right. \\&\quad \left. -(g_{2(1)}h_{(1)}+g_{2(2)}h_{(2)})s_{1} -\frac{A_{(2)}s_{1}}{2} +\frac{A_{(4)}s_{1}m}{2} \right) \\&\quad (J_{0}(\sqrt{s_{1}}R_{1})-J_{2}(\sqrt{s_{1}}R_{1} ) \\&\quad - \left( \frac{3A_{1} \sqrt{s_{1}} -3A_{3} \sqrt{s_{1}}m}{R_{1}^3} +\frac{-A_{7} \sqrt{s_{1}} +A_{8} \sqrt{s_{1}}m}{R_{1}^3}\right. \\&\quad +\frac{(c_{3(1)}I_{(1)}+c_{3(2)}I_{(2)}) \sqrt{s_{1}} }{R_{1}} -\frac{(g_{7(1)}h_{(1)}+g_{7(2)}h_{(2)}) \sqrt{s_{1}} }{R_{1}}\\&\quad \left. -\frac{(c_{3(1)}S_{(1)}+c_{3(2)}S_{(2)}) \sqrt{s_{1}} m}{R_{1}} -\frac{A_{2} \sqrt{s_{1}} }{R_{1}} +\frac{A_{4} \sqrt{s_{1}} m}{R_{1}}\right) J_{1}(\sqrt{s_{1}} R_{1}) \end{aligned} \end{aligned}$$

(107)

$$\begin{aligned} \begin{aligned} m_{50}&= -\frac{A1 s_{2}^2- A3 s_{2}^2 n}{2} \left( -\frac{3}{4}J_{0}(\sqrt{s_{2}}R_{1}) +J_{2}(\sqrt{s_{2}}R_{1})\right. \\&\quad -\frac{1}{4}J_{4}(\sqrt{s_{2}}R_{1})) - \frac{A_{(1)} s_{2}^{1.5} -A_{(3)} s_{2}^{1.5} n }{2R_{1}}\\&\quad \left( -\frac{3}{2} J_{1}(\sqrt{s_{2}} R_{1}) +\frac{1}{2} J_{3}(\sqrt{s_{2}} R_{1}) \right) \\&\quad - \left( \frac{-3A_{(1)} s_{2} +3A_{(3)} s_{2} m }{2R_{1}^{2}} +\frac{A_{(7)} s_{2} -A_{(8)} s_{2} n }{2R_{1}^{2}}\right. \\&\quad \left. -(g_{2(1)}h_{(1)}+g_{2(2)}h_{(2)})s_{2} -\frac{A_{(2)}s_{2}}{2} +\frac{A_{(4)}s_{2}n}{2} \right) \\&\quad (J_{0}(\sqrt{s_{2}}R_{1})-J_{2}(\sqrt{s_{2}}R_{1} ) \\&\quad - \left( \frac{3A_{1} \sqrt{s_{2}} -3A_{3} \sqrt{s_{2}}n}{R_{1}^3} +\frac{-A_{7} \sqrt{s_{2}} +A_{8} \sqrt{s_{2}}n}{R_{1}^3}\right. \\&\quad +\frac{(c_{3(1)}I_{(1)}+c_{3(2)}I_{(2)}) \sqrt{s_{2}} }{R_{1}} -\frac{(g_{7(1)}h_{(1)}+g_{7(2)}h_{(2)}) \sqrt{s_{2}} }{R_{1}}\\&\quad -\frac{(c_{3(1)}S_{(1)}+c_{3(2)}S_{(2)}) \sqrt{s_{2}} m}{R_{1}}\\&\quad \left. -\frac{A_{2} \sqrt{s_{2}} }{R_{1}} +\frac{A_{4} \sqrt{s_{2}} n}{R_{1}}\right) J_{1}(\sqrt{s_{2}} R_{1}) \end{aligned} \end{aligned}$$

(108)

$$\begin{aligned} \begin{aligned} m_{51}&= - 2 \left( c_{3(1)}S_{(1)}+c_{3(2)}S_{(2)}\right) -4A_{4}\\ m_{52}&= \frac{2A_{1(1)}-2A_{7(1)}}{R_{1}^3}\\ m_{53}&= \frac{2A_{1(1)}+2A_{7(1)}}{R_{1}}\\ m_{54}&= \frac{A_{1(1)}d^3}{4} (3I_{1}(dR_{1})+I_{3}(dR_{1}))\\&\quad +\frac{A_{7(1)}d^2}{2R_{1}} (I_{0}(dR_{1})+I_{2}(dR_{1}))\\&\quad -\frac{A_{7(1)}d}{R_{1}^{2}} I_{1}(dR_{1})\\ m_{55}&= \frac{A_{1(1)}d^3}{4} (-3k_{1}(dR_{1})-k_{3}(dR_{1}))\\&\quad +\frac{A_{7(1)}d^2}{2R_{1}} (k_{0}(dR_{1})+k_{2}(dR_{1}))\\&\quad +\frac{A_{7(1)}d}{R_{1}^{2}} k_{1}(dR_{1})\\ m_{56}&=-(\frac{-A_{(1)} s_{1}^{1.5} +A_{(3)} s_{1}^{1.5} m }{2}\\&\quad \left( -\frac{3}{2} J_{1}(\sqrt{s_{1}}R_{1})+\frac{1}{2} J_{3}(\sqrt{s_{1}}R_{1}) \right) \\&\quad -(\frac{A_{(8)} s_{1}m-A_{(7)} s_{1} }{2R_{1}} (J_{0}(\sqrt{s_{1}}R_{1})- J_{2}(\sqrt{s_{1}}R_{1}))\\&\quad - \frac{A_{7} \sqrt{s_{1}}-A_{8} \sqrt{s_{1}} m}{R_{1}^2}\\&\quad J_{1}(\sqrt{s_{1}}R_{1}) \end{aligned} \end{aligned}$$

(109)

$$\begin{aligned} \begin{aligned} m_{57}&=-(\frac{-A_{(1)} s_{2}^{1.5} +A_{(3)} s_{2}^{1.5} n }{2}\\&\quad \left( -\frac{3}{2} J_{1}(\sqrt{s_{2}}R_{1})+\frac{1}{2} J_{3}(\sqrt{s_{2}}R_{1}) \right) \\&\quad -\left( \frac{A_{(8)} s_{2}n-A_{(7)} s_{2} }{2R_{1}} ( J_{0}(\sqrt{s_{2}}R_{1})- J_{2}(\sqrt{s_{2}}R_{1}) \right) \\&\quad - \frac{A_{7} \sqrt{s_{2}}-A_{8} \sqrt{s_{2}} n}{R_{1}^2}\\&\quad J_{1}(\sqrt{s_{2}}R_{1}) \end{aligned} \end{aligned}$$

(110)

$$\begin{aligned} \begin{aligned} m_{58}&= \frac{-A_{3} s_{1}^{2} +A_{5} s_{1}^{2} m }{2} \\&\quad \left( -\frac{3}{4} J_{0}(\sqrt{s_{1}}R_{1})+ J_{2}(\sqrt{s_{1}}R_{1}) -\frac{1}{4} J_{4}(\sqrt{s_{1}}R_{1}) \right) \\&\quad + \frac{-A_{3} s_{1}^{1.5} +A_{5} s_{1}^{1.5} m }{2R_{1}} \\&\quad \left( -\frac{3}{2} J_{1}(\sqrt{s_{1}}R_{1})+\frac{1}{2} J_{3}(\sqrt{s_{1}}R_{1}) \right) \\&\quad + \left( \frac{3A_{(3)} s_{1}-3A_{5} s_{1} m }{2R_{1}^{2}}\right. \\&\quad \left. +\frac{-A_{8} s_{1}+A_{9} s_{1} m }{2R_{1}^{2}} +\frac{A_{4} s_{1}}{2} -\frac{A_{6} s_{1} m}{2}\right) \\&\quad ( J_{0}(\sqrt{s_{1}}R_{1})- J_{2}(\sqrt{s_{1}}R_{1}) ) \\&\quad +\left( \frac{-3A_{3} s_{1}^{0.5}+3A_{5} s_{1}^{0.5} m }{R_{1}^{3}} + \frac{A_{8} s_{1}^{0.5}-A_{9} s_{1}^{0.5} m }{R_{1}^{3}} \right. \\&\quad -\frac{(c_{3(1)}S_{(1)}+c_{3(2)}S_{(2)}) \sqrt{s_{1}} }{R_{1}} +\frac{(c_{3(1)}h_{(1)}+c_{3(2)}h_{(2)}) \sqrt{s_{1}}m }{R_{1}} \\&\quad \left. +\frac{A_{4} \sqrt{s_{1}} }{R_{1}} -\frac{A_{6} \sqrt{s_{1}}m }{R_{1}}\right) J_{1}(\sqrt{s_{1}}R_{1}) \end{aligned} \end{aligned}$$

(111)

$$\begin{aligned} \begin{aligned} m_{59}&= \frac{-A_{3} s_{2}^{2} +A_{5} s_{2}^{2} n }{2}\\&\quad \left( -\frac{3}{4} J_{0}(\sqrt{s_{2}}R_{1})+ J_{2}(\sqrt{s_{2}}R_{1}) -\frac{1}{4} J_{4}(\sqrt{s_{2}}R_{1}) \right) \\&\quad + \frac{-A_{3} s_{2}^{1.5} +A_{5} s_{2}^{1.5} n }{2R_{1}} \left( -\frac{3}{2} J_{1}(\sqrt{s_{2}}R_{1})+\frac{1}{2} J_{3}(\sqrt{s_{2}}R_{1})\right) \\&\quad + \left( \frac{3A_{(3)} s_{2}-3A_{5} s_{2} m }{2R_{1}^{2}} +\frac{-A_{8} s_{2}+A_{9} s_{2} n }{2R_{1}^{2}}\right. \\&\quad \left. +\frac{A_{4} s_{2}}{2} -\frac{A_{6} s_{2} n}{2} \right) ( J_{0}(\sqrt{s_{2}}R_{1})- J_{2}(\sqrt{s_{2}}R_{1}) ) \\&\quad + \left( \frac{-3A_{3} s_{2}^{0.5}+3A_{5} s_{2}^{0.5} m }{R_{1}^{3}} + \frac{A_{8} s_{2}^{0.5}-A_{9} s_{2}^{0.5} m }{R_{1}^{3}} \right. \\&\quad -\frac{(c_{3(1)}S_{(1)}+c_{3(2)}S_{(2)}) \sqrt{s_{2}} }{R_{1}} +\frac{(c_{3(1)}h_{(1)}+c_{3(2)}h_{(2)}) \sqrt{s_{2}}n }{R_{1}}\\&\quad \left. +\frac{A_{4} \sqrt{s_{2}} }{R_{1}} -\frac{A_{6} \sqrt{s_{2}}n }{R_{1}}\right) J_{1}(\sqrt{s_{2}}R_{1}) \end{aligned} \end{aligned}$$

(112)

$$\begin{aligned} \begin{aligned} m_{60}&=2(c_{3(1)}S_{(1)}+c_{3(2)}S_{(2)})-4A_{4}\\ m_{61}&=4A_{6}-2(c_{3(1)}h_{(1)}+c_{3(2)}h_{(2)})\\ m_{62}&=\frac{A_{(3)} s_{1}^{1.5}-A_{5} s_{1}^{1.5} m }{2}\\&\quad (-\frac{3}{2} J_{1}(\sqrt{s_{1}}R_{1})+ \frac{1}{2}J_{3}(\sqrt{s_{1}}R_{1}) +\frac{A_{8} s_{1}-A_{9} s_{1} m }{2R_{1}}\\&\quad (J_{0}(\sqrt{s_{1}}R_{1})-J_{2}(\sqrt{s_{1}}R_{1} ) \\&\quad + \left( \frac{-A_{8} \sqrt{s_{1}}+A_{9} \sqrt{s_{1}} m }{R_{1}^{2}} \right) J_{1}(\sqrt{s_{1}}R_{1}) ) \end{aligned} \end{aligned}$$

(113)

$$\begin{aligned} \begin{aligned} m_{63}&=\frac{A_{(3)} s_{2}^{1.5}-A_{5} s_{2}^{1.5} n }{2}\\&\quad \left( -\frac{3}{2} J_{1}(\sqrt{s_{2}}R_{1})+ \frac{1}{2}J_{3}(\sqrt{s_{2}}R_{1}) +\frac{A_{8} s_{2}-A_{9} s_{2} n }{2R_{1}}\right. \\&\quad (J_{0}(\sqrt{s_{2}}R_{1})-J_{2}(\sqrt{s_{2}}R_{1} )\\&\quad + \left( \frac{-A_{8} \sqrt{s_{2}}+A_{9} \sqrt{s_{2}} n }{R_{1}^{2}} \right) J_{1}(\sqrt{s_{2}}R_{1}) ) \end{aligned} \end{aligned}$$

(114)

The vector D in Eq. (74) is given as

$$\begin{aligned} \left[ D \right] = \left[ \begin{array}{ccccccccccc} 0 &{}0 &{}0 &{}m_{64} &{} m_{65} &{} m_{66} &{} m_{67} &{} m_{68} &{} m_{69} &{} m_{70} &{} m_{71} \\ \end{array} \right] \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} m_{64}&=t_{0} R_{1}^4 \quad m_{65}=4t_{0} R_{1}^3 \\ m_{66}&=12t_{0} R_{1}^2\quad m_{67}=-32A_{2}t_{0}R_{1}+8A_{4}t_{1}R_{1}\\ m_{68}&=-24A_{1}t_{0}+6A_{3}t_{1}+2A_{8}t_{1}-8A_{7}t_{0}-(c_{3(1)}I_{(1)}\\&\quad +c_{3(2)}I_{(2)}) 4 R_{1}^2 t_{0}\\&\quad +(g_{7(2)}h_{2}+g_{7(1)}h_{1})4 R_{1}^2 t_{0}+(c_{3(2)}S_{2}+c_{3(1)}S_{1}) R_{1}^2 t_{1}\\&\quad +24 t_{0}(g_{2(2)}h_{2}+g_{2(1)}h_{1}) R_{1}^2\\&\quad +16t_{0} R_{1}^2 A2-16t_{3} R_{1}^2 A_{4}\\ m_{69}&=24t_{0}R_{1}A_{1}+8t_{0}R_{1}A_{7}-6t_{1}R_{1}A_{3}-2t_{1}R_{1}A_{8}\\ m_{70}&=-24A_{3}t_{0}+6A_{5}t_{1}-8A_{8}t_{0}+2A_{9}t_{1}\\&\quad -(c_{3(2)}S_{(2)}+c_{3(1)}S_{(1)}) 4 R_{1}^2 t_{0}\\&\quad +(c_{3(2)}h_{2}+c_{3(1)}h_{1}) R_{1}^2 t_{1} +16t_{0} R_{1}^2 A_{4}-16t_{3} R_{1}^2 A_{6}\\ m_{71}&=24t_{0}R_{1}A_{3}+8t_{0}R_{1}A_{8}-6t_{1}R_{1}A_{5}-2t_{1}R_{1}A_{9}\\ t_{0}&=\frac{q A_{6}}{64(A_{2}A_{6}-A_{4}^{2} )} \\ t_{1}&=\frac{q A_{4}}{16(A_{2}A_{6}-A_{4}^{2} )}\\ t_{3}&=\frac{q A_{4}}{64(A_{2}A_{6}-A_{4}^{2} )} \end{aligned} \end{aligned}$$

(115)