A nodal spacing study on the frequency convergence characteristics of structural free vibration analysis by lumped mass Lagrangian finite elements

Abstract

The frequency convergence rate of 2p is a standard result for finite element analysis of structural free vibrations, where p is the degree of shape functions. Nonetheless, it is theoretically shown in this study that for high order Lagrangian finite elements with equally spaced nodes, this desirable or optimal convergence rate can not be achieved by the lumped mass formulation. The lumped mass matrices for Lagrangian elements are formulated herein via the commonly used row-sum technique. A set of analytical frequency error measures is presented for one-dimensional cubic through sextic elements, which elucidates that these exists convergence limits for the vibration frequencies produced by the lumped mass finite element analysis with equally spaced nodes. More specifically, the frequency convergence rates are limited to 4 for odd degree elements, and 6 for even degree elements, respectively. It also turns out that for high order finite elements with equally spaced nodes, an increase of the shape function degree may deteriorate the frequency convergence rate and accuracy, rather than improve the convergence performance as expected, which attributes to the Runge phenomena associated with the Lagrangian shape functions using equally spaced nodes. On the other hand, the lumped mass Lagrangian elements which employ the Lobatto points as nodes, ensure an optimal frequency convergence regardless of the element degree. These theoretical results are well demonstrated by numerical examples.

Appendix

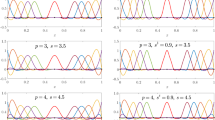
For completeness of this study, as shown in Fig. 26, the quartic to sextic shape functions of Lobatto elements are plotted to compare with the same degree shape functions of Lagrangian finite elements with equally spaced nodes given in Fig. 1. It is clear that Lobatto elements eliminate the oscillating Runge phenomena near the element boundaries.

Fig. 26

Schematic illustration of the shape functions for quartic through sextic Lobatto elements

It is noted that in Fig. 10, identical convergence results are observed for the fixed–fixed rod problem using the consistent mass Lagrangian elements with equally spaced nodes and Lobatto elements. To explain the reason underlying this observation, through a lengthy but straightforward derivation, the following analytical frequency error estimates are attained for cubic through sextic elements:

$$\left\{ \begin{gathered} e_{{es - CM}}^{[3]} = e_{Lobatto - CM}^{[3]} \approx \frac{1}{{{201600}}}(kh)_{{}}^{6} + {\mathcal{O}}(h_{{}}^{8} ) \hfill \\ e_{{es- CM}}^{[4]} = e_{Lobatto - CM}^{[4]} \approx \frac{1}{{50803200}}(kh)_{{}}^{8} + {\mathcal{O}}(h_{{}}^{10} ) \hfill \\ e_{{es - CM}}^{[5]} = e_{Lobatto - CM}^{[5]} \approx \frac{1}{{20118067200}}(kh)_{{}}^{10} + {\mathcal{O}}(h_{{}}^{12} ) \hfill \\ e_{{es - CM}}^{[6]} = e_{Lobatto - CM}^{[6]} \approx \frac{1}{{11507534438400}}(kh)_{{}}^{12} + {\mathcal{O}}(h_{{}}^{14} ) \hfill \\ \end{gathered} \right.,$$

(97)

where $e_{{es- CM}}^{[p]}$ and $e_{Lobatto - CM}^{[p]}$ represent the frequency errors for the pth degree consistent mass Lagrangian elements with equally spaced nodes and Lobatto elements.

In accordance with the analytical frequency accuracy measures in Eq. (97), it is evident that the frequency errors of the consistent mass Lagrangian elements with equally spaced nodes and Lobatto elements are exactly the same, although their shape functions are different. However, it turns out that the stiffness matrices of Lagrangian elements with equally spaced nodes have much larger condition numbers in comparison with the Lobatto elements. This point is further illustrated in Figs. 27 and 28 using the fixed–fixed rod problem with 61 DOFs. In Fig. 27, it can be seen that for both types of elements, the condition numbers of consistent and lumped mass matrices are much smaller than the condition numbers of stiffness matrices, and the condition numbers of stiffness matrices for the Lagrangian elements with equally spaced nodes are far beyond those of the Lobatto elements’ stiffness matrices and grow very quickly as the basis degree increases [43]. The superior conditional property of Lobatto elements is further demonstrated in Fig. 28 for the product matrices formulated through multiplying the inverse of mass matrices by the stiffness matrices. These product matrices provide the standard eigenvalue problems to extract the free vibration frequencies. The ill-conditioned issue of Lagrangian elements with equally spaced nodes poses severe numerical difficulty to employ high order elements, even for consistent mass matrices.

Fig. 27

Condition number comparison for the stiffness and mass matrices of Lagrangian elements with equally spaced nodes and Lobatto elements

Fig. 28

Condition number comparison for the mass inverse-stiffness product matrices of Lagrangian elements with equally spaced nodes and Lobatto elements