Skip to main content
SpringerLink
Log in

Nonlocal dynamic response analysis of functionally graded porous L-shape nanoplates resting on elastic foundation using finite element formulation

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

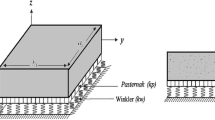
This paper proposes a finite element method (FEM) based on a nonlocal theory for the dynamic response analysis of the functionally graded porous (FGP) L-shape nanoplate lying on the elastic foundation (EF). The FGP nanoplate with uneven porosity distribution includes two parameters as the power-law index (\(k\)) and the porosity factor (\(\xi\)). The EF is Pasternak’s model with two parameters: the spring stiffness (\(k_{1}\)) and the shear layer stiffness (\(k_{2}\)). For the first time, the motion equation of FGP nanoplates is established using an eight-node rectangular element (Q8). Some numerical results in our work are compared with other published to verify accuracy and reliability. Moreover, the influence of geometric parameters, material properties on the vibration response of the FGP nanoplates resting on the EF is comprehensively investigated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Bunch JS, Van der AM, Verbridge SS, Frank IW, Tanenbsum DM, Parpia JM (2007) Electromechanical resonators from graphene sheets. Science 315:490–493

    Google Scholar 

  2. Freund LB, Suresh S (2003) Thin film materials. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  3. Sakhaee-Pour A, Ahmadian MT, Vafai A (2008) Applications of single-layered graphene sheets as mass sensors and atomistic dust detectors. Solid State Commun 145:168–172

    Google Scholar 

  4. Lu G, Ocola LE, Chen J (2009) Reduced graphene oxide for room-temperature gas sensors. Nanotechnology 20:445–502

    Google Scholar 

  5. Yang F, Chong A, Lam DCC, Tong P (2002) Couple stress based strain gradient theory for elasticity. Int J Solids Struct 39(10):2731–2743

    MATH  Google Scholar 

  6. Aifantis EC (1999) Strain gradient interpretation of size effects, fracture scaling, 299–314. Springer, New York

    Google Scholar 

  7. Eringen AC (1983) On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys 54(9):4703–4710

    Google Scholar 

  8. Eringen AC (2002) Nonlocal continuum field theories. Springer, New York

    MATH  Google Scholar 

  9. Li C, Lim CW, Yu J (2011) Twisting statics and dynamics for circular elastic nanosolids by nonlocal elasticity theory. Acta Mech Solida Sin 24(6):484–494

    Google Scholar 

  10. Ansari R, Sahmani S, Arash B (2010) Nonlocal plate model for free vibrations of single-layered graphene sheets. Phys Lett A 375(1):53–62

    Google Scholar 

  11. Asemi SR, Farajpour A (2014) Decoupling the nonlocal elasticity equations for thermo-mechanical vibration of circular graphene sheets including surface effects. Phys E 60:80–90

    Google Scholar 

  12. Jalali S, Jomehzadeh E, Pugno N (2016) Influence of out-of-plane defects on vibration analysis of graphene: molecular dynamics and non-local elasticity approaches. Superlattic Microstruct 91:331–344

    Google Scholar 

  13. Pradhan S, Murmu T (2009) Small scale effect on the buckling of single-layered graphene sheets under biaxial compression via nonlocal continuum mechanics. Comput Mater Sci 47(1):268–274

    Google Scholar 

  14. Reddy J (2010) Nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates. Int J Eng Sci 48(11):1507–1518

    MathSciNet  MATH  Google Scholar 

  15. Prandhan SC, Phadikar JK (2011) Nonlocal theory for buckling of nano-plates. Int J Struct Stab Dyn 11(3):411–429

    MathSciNet  Google Scholar 

  16. Farajpour A, Danesh M, Mohammadi M (2011) Buckling analysis of variable thickness nanoplates using nonlocal continuum mechanics. Phys E 44(3):719–727

    Google Scholar 

  17. Murmu T, Adhikari S (2011) Nonlocal vibration of bonded double-nanoplate-systems. Compos B Eng 42(7):1901–1911

    Google Scholar 

  18. Aksencer T, Aydogdu M (2012) Forced transverse vibration of nanoplates using nonlocal elasticity. Phys E 44(7–8):1752–1759

    Google Scholar 

  19. Satish N, Narendar S, Gopalakrishnan S (2012) Thermal vibration analysis of orthotropic nanoplates based on nonlocal continuum mechanics. Phys E 44(9):1950–1962

    Google Scholar 

  20. Shen Z-B, Tang H-L, Li D-K, Tang G-J (2012) Vibration of single-layered graphene sheet-based nanomechanical sensor via nonlocal Kirchhoff plate theory. Comput Mater Sci 61:200–205

    Google Scholar 

  21. Hosseini-Hashemi S, Zare M, Nazemnezhad R (2013) An exact analytical approach for free vibration of Mindlin rectangular nano-plates via nonlocal elasticity. Compos Struct 100:290–299

    Google Scholar 

  22. Fazelzadeh SA, Ghavanloo E (2014) Nanoscale mass sensing based on vibration of single-layered graphene sheet in thermal environments. Acta Mech Sin 30(1):84–91

    MathSciNet  MATH  Google Scholar 

  23. Tran TT, Tran VK, Pham Q-H, Zenkour AM (2021) Extended four-unknown higher-order shear deformation nonlocal theory for bending, buckling and free vibration of functionally graded porous nanoshell resting on elastic foundation. Compos Struct 264:113737

    Google Scholar 

  24. Tran V-K, Tran T-T, Phung M-V, Pham Q-H, Nguyen-Thoi T (2020) A finite element formulation and nonlocal theory for the static and free vibration analysis of the sandwich functionally graded nanoplates resting on elastic foundation. J Nanomater 2020:1–20

    Google Scholar 

  25. Pham Q-H, Tran VK, Tran TT, Nguyen-Thoi T, Nguyen P-C (2021) A nonlocal quasi-3D theory for thermal free vibration analysis of functionally graded material nanoplates resting on elastic foundation. Case Stud Therm Eng 26:101170

    Google Scholar 

  26. Pham Q-H, Tran TT, Tran VK, Nguyen P-C, Nguyen-Thoi T (2022) Free vibration of functionally graded porous non-uniform thickness annular-nanoplates resting on elastic foundation using ES-MITC3 element. Alex Eng J 61(3):1788–1802

    Google Scholar 

  27. Doan TL, Le PB, Tran TT, Trai VK, Pham QH (2021) Free vibration analysis of functionally graded porous nano-plates with different shapes resting on elastic foundation. J Appl Comput Mech 7:1593–1605

    Google Scholar 

  28. Liu C, Yu J, Xu W, Zhang X, Wang X (2021) Dispersion characteristics of guided waves in functionally graded anisotropic micro/nano-plates based on the modified couple stress theory. Thin-Wall Struct 161:107527

    Google Scholar 

  29. Phung-Van P, Thai CH (2021) A novel size-dependent nonlocal strain gradient isogeometric model for functionally graded carbon nanotube-reinforced composite nanoplates. Eng Comput:1–14. https://doi.org/10.1007/s00366-021-01353-3

  30. Phung-Van P, Lieu QX, Nguyen-Xuan H, Wahab MA (2017) Size-dependent isogeometric analysis of functionally graded carbon nanotube-reinforced composite nanoplates. Compos Struct 166:120–135

    Google Scholar 

  31. Xinran Z, Huang M, Dongqi A, Zhou C, Li R (2021) New analytic bending, buckling, and free vibration solutions of rectangular nanoplates by the symplectic superposition method. Sci Rep (Nature Publisher Group) 11(1):1-16

  32. Ho DT, Park S-D, Kwon S-Y, Park K, Kim SY (2014) Negative Poisson’s ratios in metal nanoplates. Nat Commun 5(1):1–8

    Google Scholar 

  33. Ke L-L, Wang Y-S, Yang J, Kitipornchai S (2014) Free vibration of size-dependent magneto-electro-elastic nanoplates based on the nonlocal theory. Acta Mech Sin 30(4):516–525

    MathSciNet  MATH  Google Scholar 

  34. Malekzadeh P, Haghighi MG, Shojaee M (2014) Nonlinear free vibration of skew nanoplates with surface and small scale effects. Thin-Wall Struct 78:48–56

    Google Scholar 

  35. Lee Z, Ophus C, Fischer L, Nelson-Fitzpatrick N, Westra K, Evoy S, Radmilovic V, Dahmen U, Mitlin D (2006) Metallic NEMS components fabricated from nanocomposite Al-Mo films. Nanotechnology 17(12):3063

    Google Scholar 

  36. Simsek M (2012) Nonlocal effects in the free longitudinal vibration of axially functionally graded tapered nanorods. Comput Mater Sci 61:257–265

    Google Scholar 

  37. Simsek M, Yurtcu H (2013) Analytical solutions for bending and buckling of functionally graded nanobeams based on the nonlocal Timoshenko beam theory. Compos Struct 97:378–386

    Google Scholar 

  38. Natarajan S, Chakraborty S, Thangavel M, Bordas S, Rabczuk T (2012) Size-dependent free flexural vibration behavior of functionally graded nanoplates. Comput Mater Sci 65:74–80

    Google Scholar 

  39. Nazemnezhad R, Hosseini-Hashemi S (2014) Nonlocal nonlinear free vibration of functionally graded nanobeams. Compos Struct 110:192–199

    MATH  Google Scholar 

  40. Hosseini-Hashemi S, Nahas I, Fakher M, Nazemnezhad R (2014) Surface effects on free vibration of piezoelectric functionally graded nanobeams using nonlocal elasticity. Acta Mech 225(6):1555–1564

    MathSciNet  MATH  Google Scholar 

  41. Hosseini-Hashemi S, Nazemnezhad R, Bedroud M (2014) Surface effects on nonlinear free vibration of functionally graded nanobeams using nonlocal elasticity. Appl Math Model 38(14):3538–3553

    MathSciNet  MATH  Google Scholar 

  42. Jung W-Y, Han S-C (2013) Analysis of sigmoid functionally graded material (S-FGM) nanoscale plates using the nonlocal elasticity theory. Math Probl Eng 2013:1–10

    MathSciNet  MATH  Google Scholar 

  43. Nami MR, Janghorban M, Damadam M (2015) Thermal buckling analysis of functionally graded rectangular nanoplates based on nonlocal third-order shear deformation theory. Aerosp Sci Technol 41:7–15

    Google Scholar 

  44. Hosseini-Hashemi S, Bedroud M, Nazemnezhad R (2013) An exact analytical solution for free vibration of functionally graded circular/annular Mindlin nanoplates via nonlocal elasticity. Compos Struct 103:108–118

    MATH  Google Scholar 

  45. Salehipour H, Nahvi H, Shahidi A (2015) Exact analytical solution for free vibration of functionally graded micro/nanoplates via three-dimensional nonlocal elasticity. Phys E 66:350–358

    Google Scholar 

  46. Salehipour H, Shahidi A, Nahvi H (2015) Modified nonlocal elasticity theory for functionally graded materials. Int J Eng Sci 90:44–57

    MathSciNet  MATH  Google Scholar 

  47. Ansari R, Shojaei MF, Shahabodini A, Bazdid-Vahdati M (2015) Three-dimensional bending and vibration analysis of functionally graded nanoplates by a novel differential quadrature-based approach. Compos Struct 131:753–764

    Google Scholar 

  48. Pham QH, Nguyen PC, Tran TT, Nguyen-Thoi T (2021) Free vibration analysis of nanoplates with auxetic honeycomb core using a new third-order finite element method and nonlocal elasticity theory. Eng Comput:1–19. https://doi.org/10.1007/s00366-021-01531-3

  49. Pham Q-H, Nguyen P-C, Tran TT (2022) Dynamic response of porous functionally graded sandwich nanoplates using nonlocal higher-order isogeometric analysis. Compos Struct 290:115565

    Google Scholar 

  50. Wang Y-Z, Li F-M (2012) Static bending behaviors of nanoplate embedded in elastic matrix with small scale effects. Mech Res Commun 41:44–48

    Google Scholar 

  51. Narendar S, Gopalakrishnan S (2012) Nonlocal continuum mechanics based ultrasonic flexural wave dispersion characteristics of a monolayer graphene embedded in polymer matrix. Compos B Eng 43(8):3096–3103

    Google Scholar 

  52. Pouresmaeeli S, Ghavanloo E, Fazelzadeh S (2013) Vibration analysis of viscoelastic orthotropic nanoplates resting on viscoelastic medium. Compos Struct 96:405–410

    Google Scholar 

  53. Zenkour A, Sobhy M (2013) Nonlocal elasticity theory for thermal buckling of nanoplates lying on Winkler-Pasternak elastic substrate medium. Phys E 53:251–259

    Google Scholar 

  54. Pham Q-H, Tran TT, Tran VK, Nguyen P-C, Nguyen-Thoi T, Zenkour AM (2021) Bending and hygro-thermo-mechanical vibration analysis of a functionally graded porous sandwich nanoshell resting on elastic foundation. Mech Adv Mater Struct 2021:1–21

    Google Scholar 

  55. Daikh AA, Zenkour AM (2020) Bending of functionally graded sandwich nanoplates resting on pasternak foundation under different boundary conditions. J Appl Comput Mech 6:1245-1259

  56. Ebrahimi F, Dabbagh A, Rabczuk T (2021) On wave dispersion characteristics of magnetostrictive sandwich nanoplates in thermal environments. Eur J Mech A Solids 85:104130

    MathSciNet  MATH  Google Scholar 

  57. Zenkour A, Radwan A (2021) A compressive study for porous FG curved nanobeam under various boundary conditions via a nonlocal strain gradient theory. Eur Phys J Plus 136:248

    Google Scholar 

  58. Zenkour A, Radwan A (2020) Nonlocal mixed variational formula for orthotropic nanoplates resting on elastic foundations. Eur Phys J Plus 135:1–19

    Google Scholar 

  59. Barati MR, Faleh NM, Zenkour AM (2019) Dynamic response of nanobeams subjected to moving nanoparticles and hygro-thermal environments based on nonlocal strain gradient theory. Mech Adv Mater Struct 26:1661–1669

    Google Scholar 

  60. Panyatong M, Chinnaboon B, Chucheepsakul S (2015) Incorporated effects of surface stress and nonlocal elasticity on bending analysis of nanoplates embedded in an elastic medium. Suranaree J Sci Technol 22(1):21–33

    Google Scholar 

  61. Alazwari MA, Zenkour AM (2022) A quasi-3D refined theory for the vibration of functionally graded plates resting on Visco-Winkler-Pasternak foundations. Mathematics 10:716

    Google Scholar 

  62. Zenkour AM, Aljadani MH (2022) Buckling response of functionally graded porous plates due to a quasi-3D refined theory. Mathematics 10:565

    Google Scholar 

  63. Tran TT, Pham Q-H, Nguyen-Thoi T (2020) Dynamic analysis of functionally graded porous plates resting on elastic foundation taking into mass subjected to moving loads using an edge-based smoothed finite element method. Shock Vib 2020:1–19

    Google Scholar 

  64. Nguyen P-C, Pham QH, Tran TT, Nguyen-Thoi T (2022) Effects of partially supported elastic foundation on free vibration of FGP plates using ES-MITC3 elements. Ain Shams Eng J 13:101615

    Google Scholar 

  65. Boutaleb S, Benrahou KH, Bakora A, Algarni A, Bousahla AA, Tounsi A, Tounsi A, Mahmoud S (2019) Dynamic analysis of nanosize FG rectangular plates based on simple nonlocal quasi 3D HSDT. Adv Nano Res 7(3):191

    Google Scholar 

  66. Liu C-C, Chen Z-B (2014) Dynamic analysis of finite periodic nanoplate structures with various boundaries. Phys E 60:139–146

    Google Scholar 

  67. Nami MR, Janghorban M (2015) Dynamic analysis of isotropic nanoplates subjected to moving load using state-space method based on nonlocal second order plate theory. J Mech Sci Technol 29(6):2423–2426

    Google Scholar 

  68. Martin O (2019) Nonlocal effects on the dynamic analysis of a viscoelastic nanobeam using a fractional Zener model. Appl Math Model 73:637–650

    MathSciNet  MATH  Google Scholar 

  69. Hashemi SH, Khaniki HB (2018) Dynamic response of multiple nanobeam system under a moving nanoparticle. Alex Eng J 57(1):343–356

    Google Scholar 

  70. Lu P (2007) Dynamic analysis of axially prestressed micro/nanobeam structures based on nonlocal beam theory. J Appl Phys 101(7):073504

    Google Scholar 

  71. Shahsavari D, Shahsavari M, Li L, Karami B (2018) A novel quasi-3D hyperbolic theory for free vibration of FG plates with porosities resting on Winkler/Pasternak/Kerr foundation. Aerosp Sci Technol 72:134–149

    Google Scholar 

  72. Reddy JN (2019) Introduction to the finite element method. McGraw-Hill Education, New York

    Google Scholar 

  73. Nguyen H-N, Canh TN, Thanh TT, Ke TV, Phan V-D, Thom DV (2019) Finite element modelling of a composite shell with shear connectors. Symmetry 11(4):527

    MATH  Google Scholar 

  74. Nguyen H-N, Nguyen T-Y, Tran KV, Tran TT, Nguyen T-T, Phan V-D, Do TV (2019) A finite element model for dynamic analysis of triple-layer composite plates with layers connected by shear connectors subjected to moving load. Materials 12(4):598

    Google Scholar 

  75. Roque C, Cunha D, Shu C, Ferreira A (2011) A local radial basis functions-finite differences technique for the analysis of composite plates. Eng Anal Bound Elem 35(3):363–374

    MathSciNet  MATH  Google Scholar 

  76. Thai CH, Nguyen-Xuan H, Bordas SPA, Nguyen-Thanh N, Rabczuk T (2015) Isogeometric analysis of laminated composite plates using the higher-order shear deformation theory. Mech Adv Mater Struct 22(6):451–469

    Google Scholar 

  77. Belkorissat I, Houari MSA, Tounsi A, Bedia E, Mahmoud S (2015) On vibration properties of functionally graded nano-plate using a new nonlocal refined four variable model. Steel Compos Struct 18(4):1063–1081

    Google Scholar 

  78. Aghababaei R, Reddy J (2009) Nonlocal third-order shear deformation plate theory with application to bending and vibration of plates. J Sound Vib 326(1–2):277–289

    Google Scholar 

  79. Qian LF (2003) Free and forced vibrations of thick rectangular plates using higher-order sheara and normal deformable plate theory and meshless Petrov-Galerkin (MLPG) method. CMES 5:519–534

    MATH  Google Scholar 

Download references

Funding

The authors received no financial support for the research, authorship, and publication of this article.

Author information

Authors and Affiliations

  1. Faculty of Mechanical Engineering, Le Quy Don Technical University, Hanoi, Vietnam

    Trung Thanh Tran & Pham Binh Le

Authors
  1. Trung Thanh Tran
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pham Binh Le
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Trung Thanh Tran.

Ethics declarations

Conflict of interest

The authors declared no potential conflicts of interest with respect to the research, authorship, and publication of this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix 1

Appendix 1

The Lagrange interpolation in Eq. (25):

$$\begin{array}{*{20}l} {\aleph_{1} = \frac{1}{4}\left( {1 - r} \right)\left( {1 - s} \right)\left( { - r - s - 1} \right);{ }\aleph_{2} = \frac{1}{2}\left( {1 - r^{2} } \right)\left( {1 - s} \right);} \hfill \\ {\aleph_{3} = \left( {1 + r} \right)\left( {1 - s} \right)\left( { - r - s - 1} \right);{ } \aleph_{4} = \frac{1}{2}\left( {1 + r} \right)\left( {1 - s^{2} } \right);} \hfill \\ {\aleph_{5} = \frac{1}{4}\left( {1 + r} \right)\left( {1 + s} \right)\left( {r + s - 1} \right);{ } \aleph_{6} = \frac{1}{2}\left( {1 - r^{2} } \right)\left( {1 + s} \right);} \hfill \\ {\aleph_{7} = \frac{1}{4}\left( {1 - r} \right)\left( {1 + s} \right)\left( { - r + s - 1} \right);{ }\aleph_{8} = \frac{1}{2}\left( {1 - r} \right)\left( {1 - s^{2} } \right),} \hfill \\ \end{array}$$

with \(r, s\) are natural coordinates.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tran, T.T., Le, P.B. Nonlocal dynamic response analysis of functionally graded porous L-shape nanoplates resting on elastic foundation using finite element formulation. Engineering with Computers 39, 809–825 (2023). https://doi.org/10.1007/s00366-022-01679-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-022-01679-6

Keywords

Search

Navigation