Skip to main content

Advertisement

Springer Nature Link
Log in

An isogeometric analysis-based topology optimization framework for 2D cross-flow heat exchangers with manufacturability constraints

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

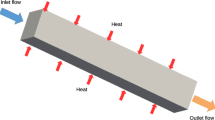
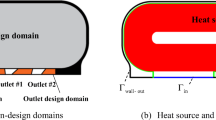
Abstract

Heat exchangers (HXs) have gained increasing attention due to the intensive demand of performance improving and energy saving for various equipment and machines. As a natural application, topology optimization has been involved in the structural design of HXs aiming at improving heat exchange performance (HXP) and meanwhile controlling pressure drop (PD). In this paper, a novel multiphysics-based topology optimization framework is developed to maximize the HXP for 2D cross-flow HXs, and concurrently limit the PD between the fluid inlet and outlet. In particular, an isogeometric analysis solver is developed to solve the coupled steady-state Navier–Stokes and heat convection–diffusion equations. Non-body-fitted control mesh is adopted instead of dynamically remeshing the design domain during the evolution of the boundary interface. The method of moving morphable voids is employed to represent and track boundary interface between the hot and the remaining regions. In addition, various constraints are incorporated to guarantee manufacturability of the optimized structures with respect to practical considerations in additive manufacturing, such as removing sharp corners, controlling channel perimeters, and minimizing overhangs. To implement the iterative optimization process, the method of moving asymptotes is employed. Numerical examples show that the HXP of the optimized structure is greatly improved compared with its corresponding initial design, and the PD between the fluid inlet and outlet is controlled concurrently. Moreover, a smooth boundary interface between the channel and the cold fluid, and improved manufacturability are simultaneously obtained for the optimized structures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Bendsœ MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71:197–224

    MathSciNet  MATH  Google Scholar 

  2. Bendsøe MP (1989) Optimal shape design as a material distribution problem. Struct Optim 1(4):193–202

    Google Scholar 

  3. Rozvany GIN (2009) A critical review of established methods of structural topology optimization. Struct Multidiscip Optim 37(3):217–237

    MathSciNet  MATH  Google Scholar 

  4. Sigmund O, Maute K (2013) Topology optimization approaches. Struct Multidisc Optim 48:1031–1055

    MathSciNet  Google Scholar 

  5. Holmberg E, Torstenfelt B, Klarbring A (2013) Stress constrained topology optimization. Struct Multidiscip Optim 48(1):33–47

    MathSciNet  MATH  Google Scholar 

  6. Cheng L, Liang X, Belski E, Wang X, Sietins JM, Ludwick S, To A (2018) Natural frequency optimization of variable-density additive manufactured lattice structure: theory and experimental validation. J Manuf Sci Eng 140(10):105002

    Google Scholar 

  7. Dbouk T (2017) A review about the engineering design of optimal heat transfer systems using topology optimization. Appl Therm Eng 112:841–854

    Google Scholar 

  8. Rodrigues H, Fernandes P (1995) A material based model for topology optimization of thermoelastic structures. Int J Numer Meth Eng 38:1951–1965

    MathSciNet  MATH  Google Scholar 

  9. Søndergaard MB, Pedersen CB (2014) Applied topology optimization of vibro-acoustic hearing instrument models. J Sound Vib 333(3):683–92

    Google Scholar 

  10. Liang X, To AC, Du J, Zhang YJ (2021) Topology optimization of phononic-like structures using experimental material interpolation model for additive manufactured lattice infills. Comput Methods Appl Mech Eng 377:113717

    MathSciNet  MATH  Google Scholar 

  11. Qian X, Dede EM (2016) Topology optimization of a coupled thermal-fluid system under a tangential thermal gradient constraint. Struct Multidiscip Optim 54(3):531–551

    MathSciNet  Google Scholar 

  12. Yoon GH (2010) Topological design of heat dissipating structure with forced convective heat transfer. J Mech Sci Technol 24(6):1225–1233

    Google Scholar 

  13. Alexandersen J, Andreasen CS (2020) A review of topology optimisation for fluid-based problems. Fluids 5(1):29–32

    Google Scholar 

  14. Haertel JH, Nellis GF (2017) A fully developed flow thermofluid model for topology optimization of 3D-printed air-cooled heat exchangers. Appl Therm Eng 119:10–24

    Google Scholar 

  15. Haertel JH, Engelbrecht K, Lazarov BS, Sigmund O (2018) Topology optimization of a pseudo 3D thermofluid heat sink model. Int J Heat Mass Transf 121:1073–88

    Google Scholar 

  16. Yoon GH (2010) Topology optimization for stationary fluid–structure interaction problems using a new monolithic formulation. Int J Numer Methods Eng 82:591–616

    MATH  Google Scholar 

  17. Yoon GH (2014) Stress-based topology optimization method for steady-state fluid–structure interaction problems. Comput Methods Appl Mech Eng 278:499–523

    MathSciNet  MATH  Google Scholar 

  18. Feppon F, Allaire G, Dapogny C, Jolivet P (2020) Topology optimization of thermal fluid–structure systems using body-fitted meshes and parallel computing. J Comput Phys 417:109574

    MathSciNet  MATH  Google Scholar 

  19. Lundgaard C, Sigmund O (2018) A density-based topology optimization methodology for thermoelectric energy conversion problems. Struct Multidiscip Optim 57(4):1427–1442

    MathSciNet  Google Scholar 

  20. Kobayashi H, Yaji K, Yamasaki S, Fujita K (2019) Freeform winglet design of fin-and-tube heat exchangers guided by topology optimization. Appl Therm Eng 161:114020

    Google Scholar 

  21. Mohammadi MH, Abbasi HR, Yavarinasab A, Pourrahmani H (2020) Thermal optimization of shell and tube heat exchanger using porous baffles. Appl Therm Eng 170:115005

    Google Scholar 

  22. Borrvall T, Petersson J (2003) Topology optimization of fluids in Stokes flow. Int J Numer Methods Fluids 41:77–107

    MathSciNet  MATH  Google Scholar 

  23. Gersborg HA, Sigmund O, Haber RB (2005) Topology optimization of channel flow problems. Struct Multidiscip Optim 30:181–192

    MathSciNet  MATH  Google Scholar 

  24. Challis VJ, Guest JK (2009) Level set topology optimization of fluids in stokes flow. Int J Numer Methods Eng 79:1284–1308

    MathSciNet  MATH  Google Scholar 

  25. Iga A, Nishiwaki S, Izui K, Yoshimura M (2009) Topology optimization for thermal conductors considering design-dependent effects, including heat conduction and convection. Int J Heat Mass Transf 52:2721–2732

    MATH  Google Scholar 

  26. Coffin P, Maute K (2016) Level set topology optimization of cooling and heating devices using a simplified convection model. Struct Multidiscip Optim 53(5):985–1003

    Google Scholar 

  27. Makhija DS, Beran PS (2019) Concurrent shape and topology optimization for steady conjugate heat transfer. Struct Multidisc Optim 59:919–940

    MathSciNet  Google Scholar 

  28. Feppon F, Allaire G, Dapogny C, Jolivet P (2021) Body-fitted topology optimization of 2D and 3D fluid-to-fluid heat exchangers. Comput Methods Appl Mech Eng 376:113638

    MathSciNet  MATH  Google Scholar 

  29. Kobayashi H, Yaji K, Yamasaki S, Fujita K (2021) Topology design of two-fluid heat exchange. Struct Multidiscip Optim 63(2):821–834

    MathSciNet  Google Scholar 

  30. Høghøj LC, Nørhave DR, Alexandersen J, Sigmund O, Andreasen CS (2020) Topology optimization of two fluid heat exchangers. Int J Heat Mass Transf 163:120543

    Google Scholar 

  31. Fujii D, Chen B, Kikuchi N (2001) Composite material design of two-dimensional structures using the homogenization design method. Int J Numer Methods Eng 50:2031–2051

    MathSciNet  MATH  Google Scholar 

  32. Rozvany GI, Zhou M, Birker T (1992) Generalized shape optimization without homogenization. Struct Optim 4:250–252

    Google Scholar 

  33. Rozvany GI (2009) A critical review of established methods of structural topology optimization. Struct Multidiscip Optim 37:217–237

    MathSciNet  MATH  Google Scholar 

  34. Allaire G, Jouve F, Toader AM (2004) Structural optimization using sensitivity analysis and a level-set method. J Comput Phys 194:363–393

    MathSciNet  MATH  Google Scholar 

  35. Zhuang Z, Xie YM, Zhou S (2021) A reaction diffusion-based level set method using body-fitted mesh for structural topology optimization. Comput Methods Appl Mech Eng 381:113829

    MathSciNet  MATH  Google Scholar 

  36. Querin O, Steven G, Xie Y (1998) Evolutionary structural optimisation (ESO) using a bidirectional algorithm. Eng Comput 15:1031–1048

    MATH  Google Scholar 

  37. Young V, Querin OM, Steven G, Xie Y (1999) 3D and multiple load case bi-directional evolutionary structural optimization (BESO). Struct Optim 18:183–192

    Google Scholar 

  38. Guo X, Zhang W, Zhang J, Yuan J (2016) Explicit structural topology optimization based on moving morphable components (MMC) with curved skeletons. Comput Methods Appl Mech Eng 310:711–748

    MathSciNet  MATH  Google Scholar 

  39. Gai Y, Zhu X, Zhang YJ, Hou W, Hu P (2020) Explicit isogeometric topology optimization based on moving morphable voids with closed B-spline boundary curves. Struct Multidiscip Optim 61(3):963–982

    MathSciNet  Google Scholar 

  40. Dede EM (2009) Multiphysics topology optimization of heat transfer and fluid flow systems. In: Proceedings of the COMSOL users conference, the COMSOL Conference, Boston, USA

  41. Jenkins N, Maute K (2015) Level set topology optimization of stationary fluid–structure interaction problems. Struct Multidiscip Optim 52:179–195

    MathSciNet  Google Scholar 

  42. Jenkins N, Maute K (2016) An immersed boundary approach for shape and topology optimization of stationary fluid–structure interaction problems. Struct Multidiscip Optim 54:1191–1208

    MathSciNet  Google Scholar 

  43. Li H, Kondoh T, Jolivet P, Furuta K, Yamada T, Zhu B, Izui K, Nishiwaki S (2022) Three-dimensional topology optimization of a fluid–structure system using body-fitted mesh adaption based on the level-set method. Appl Math Model 101:276–308

    MathSciNet  MATH  Google Scholar 

  44. Liu J, Gaynor AT, Chen S, Kang Z, Suresh K, Takezawa A, Li L, Kato J, Tang J, Wang CC, Cheng L, Liang X, To AC (2018) Current and future trends in topology optimization for additive manufacturing. Struct Multidiscip Optim 57(6):2457–2483

    Google Scholar 

  45. Hughes TJR, Cottrell JA, Bazilevs Y (2005) Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput Methods Appl Mech Eng 194(39–41):4135–4195

    MathSciNet  MATH  Google Scholar 

  46. Cottrell J, Hughes T, Bazilevs Y (2009) Isogeometric analysis: toward integration of CAD and FEA. Wiley, New York

    MATH  Google Scholar 

  47. Benson DJ, Bazilevs Y, Hsu MC, Hughes TJR (2010) Isogeometric shell analysis: the Reissner–Mindlin shell. Comput Methods Appl Mech Eng 199(5–8):276–289

    MathSciNet  MATH  Google Scholar 

  48. Casquero H, Liu L, Zhang Y, Reali A, Kiendl J et al (2017) Arbitrary-degree T-splines for isogeometric analysis of fully nonlinear Kirchhoff–Love shells. Comput Aided Des 82:140–153

    MathSciNet  Google Scholar 

  49. Casquero H, Wei X, Toshniwal D, Li A, Hughes TJR et al (2020) Seamless integration of design and Kirchhoff–Love shell analysis using analysis-suitable unstructured T-splines. Comput Methods Appl Mech Eng 360:112765

    MathSciNet  MATH  Google Scholar 

  50. Zhang YJ, Bazilevs Y, Goswami S, Bajaj CL, Hughes TJR (2007) Patient-specific vascular NURBS modeling for isogeometric analysis of blood flow. Comput Methods Appl Mech Eng 196(29):2943–2959

    MathSciNet  MATH  Google Scholar 

  51. Lorenzo G, Scott MA, Tew K, Hughes TJ, Zhang YJ et al (2016) Tissue-scale, personalized modeling and simulation of prostate cancer growth. PNAS 113(48):7663–7671

    Google Scholar 

  52. Zhang YJ (2016) Geometric modeling and mesh generation from scanned images. CRC Press Taylor & Francis Group, Boca Raton

    MATH  Google Scholar 

  53. Li A, Chai X, Yang G, Zhang YJ (2019) An isogeometric analysis computational platform for material transport simulation in complex neurite networks. Mol Cell Biomech 16(2):123–140

    Google Scholar 

  54. Casquero H, Bona-Casas C, Toshniwal D, Hughes TJR, Gomez H, Zhang YJ (2021) The divergence-conforming immersed boundary method: application to vesicle and capsule dynamics. J Comput Phys 425:109872

    MathSciNet  MATH  Google Scholar 

  55. Bazilevs Y, Calo VM, Zhang Y, Hughes TJR (2006) Isogeometric fluid–structure interaction analysis with applications to arterial blood flow. Comput Mech 38(4–5):310–322

    MathSciNet  MATH  Google Scholar 

  56. Bazilevs Y, Calo VM, Hughes TJR, Zhang Y (2008) Isogeometric fluid–structure interaction: theory, algorithms, and computations. Comput Mech 43(1):3–37

    MathSciNet  MATH  Google Scholar 

  57. Casquero H, Zhang YJ, Bona-Casas C, Dalcin L, Gomez H (2018) Non-body-fitted fluid–structure interaction: divergence-conforming B-splines, fully-implicit dynamics, and variational formulation. J Comput Phys 374:625–653

    MathSciNet  MATH  Google Scholar 

  58. Lai Y, Liu L, Zhang YJ, Chen J, Fang E et al (2016) Rhino 3D to Abaqus: a T-spline based isogeometric analysis software platform. The edited volume of the modeling and simulation in science, engineering and technology book series, part IV. Springer Publisher, pp 271–281

  59. Lai Y, Zhang YJ, Liu L, Wei X, Fang E et al (2017) Integrating CAD with Abaqus: a practical isogeometric analysis software platform for industrial applications. A special issue of HOFEIM 2016. Comput Math Appl 74(7):1648–1660

    MathSciNet  MATH  Google Scholar 

  60. Yu Y, Wei X, Li A, Liu JG, He J et al (2020) HexGen and Hex2Spline: polycube-based hexahedral mesh generation and unstructured spline construction for isogeometric analysis framework in LS-DYNA. Springer INdAM Serie: proceedings of INdAM Workshop “Geometric Challenges in Isogeometric Analysis”

  61. Yu Y, Liu JG, Zhang YJ (2021) HexDom: polycube-based hexahedral dominant mesh generation. The edited volume of mesh generation and adaptation: cutting-edge techniques, SEMA-SIMAI Springer Series

  62. An Z, Yu T, Bui TQ, Wang C, Trinh NA (2018) Implementation of isogeometric boundary element method for 2-D steady heat transfer analysis. Adv Eng Soft 116:36–49

    Google Scholar 

  63. Dede L, Borden MJ, Hughes TJR (2012) Topology optimization with isogeometric analysis in a phase field approach. Arch Comput Methods Eng 19(3):427–65

    MathSciNet  MATH  Google Scholar 

  64. Jahangiry HA, Tavakkoli SM (2017) An isogeometrical approach to structural level set topology optimization. Comput Methods Appl Mech Eng 319:240–257

    MathSciNet  MATH  Google Scholar 

  65. Svanberg K (1987) The method of moving asymptotes: a new method for structural optimization. Int J Numer Methods Eng 24(2):359–373

    MathSciNet  MATH  Google Scholar 

  66. Svanberg K (1993) The method of moving asymptotes (MMA) with some extensions. Optimization of Large Structural Systems. Springer, Dordrecht, pp 555–566

    Google Scholar 

  67. Zhao X, Zhou M, Liu Y, Ding M, Hu P, Zhu P (2019) Topology optimization of channel cooling structures considering thermomechanical behavior. Struct Multidiscip Optim 59:613–632

    MathSciNet  Google Scholar 

  68. Wei X, Zhang YJ, Liu L, Hughes TJR (2017) Truncated T-splines: fundamentals and methods. Comput Methods Appl Mech Eng Spec Issue Isogeom Anal 316:349–372

    MathSciNet  MATH  Google Scholar 

  69. Wei X, Zhang YJ, Hughes TJR (2017) Truncated hierarchical tricubic C0 spline construction on unstructured hexahedral meshes for isogeometric analysis applications. Comput Methods Appl Mech Eng 74(9):2203–2220

    MATH  Google Scholar 

  70. Wei X, Zhang YJ, Toshniwal D, Speleers H, Li X et al (2018) Blended B-spline construction on unstructured quadrilateral and hexahedral meshes with optimal convergence rates in isogeometric analysis. Comput Methods Appl Mech Eng 341:609–639

    MathSciNet  MATH  Google Scholar 

  71. Balay S, Abhyankar S, Adams MF, Brown J, Brune P, Buschelman K, Dalcin L, Dener A, Eijkhout V, Gropp WD, Karpeyev D et al (2019) PETSC users manual tech Rep ANL-95/11-Revision 3.11. Argonne National Laboratory

  72. Koobus B, Farhat C (2004) A variational multiscale method for the large eddy simulation of compressible turbulent flows on unstructured meshes—application to vortex shedding. Comput Methods Appl Mech Engrg 193:1367–1383

    MathSciNet  MATH  Google Scholar 

  73. Bazilevs Y, Calo VM, Cottrell JA, Hughes TJR, Reali A et al (2007) Variational multiscale residual-based turbulence modeling for large eddy simulation of incompressible flows. Comput Methods Appl Mech Eng 197(1):173–201

    MathSciNet  MATH  Google Scholar 

  74. Brooks AN, Hughes TJR (1982) Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier–Stokes equations. Comput Methods Appl Mech Eng 32(1):199–259

    MathSciNet  MATH  Google Scholar 

  75. Hughes TJR, Scovazzi G, Franca LP (2004) Multiscale and stabilized methods, in Encyclopedia of computational mechanics, computational fluid dynamics, vol 3 (chapter 4). Wiley, New York

    Google Scholar 

  76. Towns J, Cockerill T, Dahan M, Foster I, Gaither K, Grimshaw A, Hazlewood V, Lathrop S, Lifka D, Peterson GD, Roskies R, Scott JR, Wilkens-Diehr N (2014) XSEDE: accelerating scientific discovery. Comput Sci Eng 16(5):62–74

    Google Scholar 

Download references

Acknowledgements

The research in this paper was sponsored by the Army Research Laboratory and was accomplished under Cooperative Agreement Number W911NF-20-2-0175. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Laboratory or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562. Specifically, it used the Bridges-2 system, which is supported by NSF award number ACI-1928147, at the Pittsburgh Supercomputing Center (PSC).

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Carnegie Mellon University, 5000 Forbes Avenue, Pittsburgh, PA, 15213, USA

    Xuan Liang, Angran Li & Yongjie Jessica Zhang

  2. Department of Materials Science and Engineering, Carnegie Mellon University, 5000 Forbes Avenue, Pittsburgh, PA, 15213, USA

    Anthony D. Rollett

  3. The NextManufacturing Center, Carnegie Mellon University, 5000 Forbes Avenue, Pittsburgh, PA, 15213, USA

    Xuan Liang, Anthony D. Rollett & Yongjie Jessica Zhang

Authors
  1. Xuan Liang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Angran Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Anthony D. Rollett
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Yongjie Jessica Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yongjie Jessica Zhang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest. All the co-authors have confirmed to know the submission of the manuscript by the corresponding author.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liang, X., Li, A., Rollett, A.D. et al. An isogeometric analysis-based topology optimization framework for 2D cross-flow heat exchangers with manufacturability constraints. Engineering with Computers 38, 4829–4852 (2022). https://doi.org/10.1007/s00366-022-01716-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-022-01716-4

Keywords

Profiles

  1. Yongjie Jessica Zhang View author profile