Skip to main content
Springer Nature Link
Log in

Concurrent topology optimization of coated structure for non-homogeneous materials under buckling criteria

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

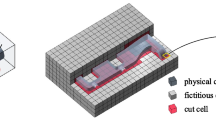
This study used an adaptive mapping technique to examine multiscale bucking optimal topology for structural coating. The adaptive geometric components (AGCs) include a framework of macro-sandwich bars representing a macrostructure with a solid coating and a group of micro-solid bars representing the nonuniform concurrent at the microstructural scale. The layout of optimized design, comprising the coated layer, and the interior microscale are together designed with buckling constraints. The properties of material change in a certain direction in response to a specified variation in the macro- and microstructures, designed using functionally graded materials. Examining the optimal AGC geometries under buckling constraints yielded a structure with asymmetric stiffness qualities. Furthermore, a comparison of different structures, including solid, lattice, and coating of concurrent structures, under buckling constraint was conducted and is presented herein. The some examples of maximizing structural stiffness, used as an objective under buckling constraints, confirm that the approach of proposed method works effectively and yields satisfactory results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30
Fig. 31
Fig. 32
Fig. 33
Fig. 34
Fig. 35

Similar content being viewed by others

References

  1. Zhang P, Toman J, Yu Y, Biyikli E, Kirca M et al (2015) Efficient design-optimization of variable-density hexagonal cellular structure by additive manufacturing: theory and validation. J Manuf Sci Eng Trans ASME 137:41–50

    Google Scholar 

  2. Wang X, Zhang P, Ludwick S, Belski E, To AC (2018) Natural frequency optimization of 3D printed variable-density honeycomb structure via a homogenization-based approach. Addit Manuf 20:189–198

    Google Scholar 

  3. Zhang W, Li D, Zhou J, Du Z, Li B, Guo X (2018) A moving morphable void (MMV)-based explicit approach for topology optimization considering stress constraint. Comput Methods Appl Mech Eng 334:381–413

    MathSciNet  MATH  Google Scholar 

  4. Wu J, Wang CCL, Zhang X, Westermann R (2016) Self-supporting rhombic infill structures for additive manufacturing. CAD Comput Aided Des 80:32–42

    Google Scholar 

  5. Hoang VN, Tran P, Nguyen NL, Xuan HN (2020) Adaptive concurrent topology optimization of coated structures with nonperiodic infill for additive manufacturing. CAD Comput Aided Des 129:1202918

    MathSciNet  Google Scholar 

  6. Bendsoe MP (1989) Optimal shape design as a material distribution problem. Struct Optim 1:193–202

    Google Scholar 

  7. Sofiyev AH (2019) Review of research on the vibration and buckling of the FGM conical shells. Compos Struct 211:301–317

    Google Scholar 

  8. Allaire G, Jouve F, Toader AM (2002) A level set method for shape optimization. C R Math 334:1125–1130

    MathSciNet  MATH  Google Scholar 

  9. Wang MY, Wang X, Guo D (2003) A level set method for structural topology optimization. Comput Methods Appl Mech Eng 192:227–246

    MathSciNet  MATH  Google Scholar 

  10. Xie YM, Steven GP (1993) A level set method for structural topology optimization. Comput Struct 49:885–896

    Google Scholar 

  11. Saxena A (2011) Topology design with negative masks using gradient search. Struct Multidiscip Optim 44:629–649

    Google Scholar 

  12. Guo X, Zhang W, Zhong W (2014) Doing topology optimization explicitly and geometrically—a new moving morphable components based framework. J Appl Mech 81:081009

    Google Scholar 

  13. Norato JA, Bell BK, Tortorelli DA (2015) A geometry projection method for continuum-based topology optimization with discrete elements. Comput Methods Appl Mech Eng 293:306–327

    MathSciNet  MATH  Google Scholar 

  14. Hoang VN, Jang GW (2017) Topology optimization using moving morphable bars for versatile thickness control. Comput Methods Appl Mech Eng 371:153–173

    MathSciNet  MATH  Google Scholar 

  15. Hoang VN, Nguyen NL, Xuan HN (2020) Topology optimization of coated structure using moving morphable sandwich bars. Struct Multidiscip Optim 61:491–506

    Google Scholar 

  16. Wang X, Long K, Hoang VN, Hu P (2018) An explicit optimization model for integrated layout design of planar multi-component systems using moving morphable bars. Comput Methods Appl Mech Eng 342:46–70

    MathSciNet  MATH  Google Scholar 

  17. Guo X, Zhou J, Zhang W, Du Z, Liu C, Liu Y (2017) Self-supporting structure design in additive manufacturing through explicit topology optimization. Comput Methods Appl Mech Eng 323:27–63

    MathSciNet  MATH  Google Scholar 

  18. Zhang W, Liu Y, Du Z, Zhu Y, Guo X (2018) A moving morphable component based topology optimization approach for rib-stiffened structures considering buckling constraints. J Mech Des 140:111404

    Google Scholar 

  19. Zhang S, Norato JA (2017) Optimal design of panel reinforcements with ribs made of plates. J Mech Des 139:081403

    Google Scholar 

  20. Liu C, Du Z, Zhang W, Zhu Y, Guo X (2017) Additive manufacturing-oriented design of graded lattive structures through explicit topology optimization. J Appl Mech 84:081008

    Google Scholar 

  21. Deng J, Pedersen CBM, Chen W (2019) Connected morphable components-based multiscale topology optimization. Front Mech Eng 14:129–140

    Google Scholar 

  22. Hoang VN, Nguyen NL, Tran P, Qian M, Xuan HN (2020) Adaptive concurrent topology optimization of cellular composites for additive manufacturing. JMO 72:2378–2390

    Google Scholar 

  23. Sivapuram R, Dunning PD, Kim HA (2016) Simultaneous material and structural optimization by multiscale topology optimization. Struct Multidiscip Optim 54:1267–1281

    MathSciNet  Google Scholar 

  24. Xia L, Breitkopf P (2014) Concurrent topology optimization design of material and structure within FE2 nonlinear multiscale analysis framework. Comput Methods Appl Mech Eng 278:524–542

    MATH  Google Scholar 

  25. Li H, Luo Z, Gao L, Qin Q (2018) Topology optimization for concurrent design of structures with multi-patch microstructures by level sets. Comput Methods Appl Mech Eng 331:536–561

    MathSciNet  MATH  Google Scholar 

  26. Yan J, Guo X, Chan G (2016) Multi-scale concurrent material and structural design under mechanical and thermal loads. Comput Mech 57:437–446

    MathSciNet  MATH  Google Scholar 

  27. Xia L, Breitkopf P (2017) Recent advances on topology optimization of multiscale nonlinear structures. Arch Comput Methods Eng 24:227–249

    MathSciNet  MATH  Google Scholar 

  28. Vincente WM, Zuo ZH, Pavanello R, Calixto TKL, Picelli R, Xie YM (2016) Concurrent topology optimization for minimizing frequency responses of two-level hierarchical structures. Comput Methods Appl Mech Eng 301:116–136

    MathSciNet  MATH  Google Scholar 

  29. Bendsoe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71:197–224

    MathSciNet  MATH  Google Scholar 

  30. Groen JP, Sigmun O (2018) Homogenization-based topology optimization for high-resolution manufacturable microstructures. Int J Numer Methods Eng 113:1148–1163

    MathSciNet  Google Scholar 

  31. Clausen A, Aage N, Sigmund O (2015) Topology optimization of coated structures and material interface problems. Comput Methods Appl Mech Eng 290:524–541

    MathSciNet  MATH  Google Scholar 

  32. Wu J, Wang W, Gao X (2019) Design and optimization of conforming lattice structures. IEEE Trans Vis Comput Graph 27

  33. Wu J, Sigmund O, Groen PJ (2021) Topology optimization of multi-scale structures: a review. Struct Multidiscip Optim 63:455–1480

    MathSciNet  Google Scholar 

  34. Clausen A, Aage N, Sigmund O (2016) Exploiting additive manufacturing infill in topology optimization for improved buckling load. Engineering 2:250–257

    Google Scholar 

  35. Youn GH, Yi B (2019) A new coating filter of coated structure for topology optimization. Struct Multidiscip Optim

  36. Wang Y, Kang Z (2018) A level set method for shape and topology optimization of coated structures. Comput Methods Appl Mech Eng 329:553–574

    MathSciNet  MATH  Google Scholar 

  37. Fu J, Li H, Xiao M, Gao L, Chu S (2019) Topology optimization of shell-infill structures using a distance regularized parametric level-set method. Struct Multidiscip Optim 59:249–262

    MathSciNet  Google Scholar 

  38. Rahmatalla S, Swan CC (2003) Continuum topology optimization of buckling-sensitive structure. AIAA J 41(6):1180–1189

    Google Scholar 

  39. Gao X, Ma H (2014) A new method for dealing with pseudo modes in topology optimization of continua for free vibration. Lixue Xuebao/Chin J Theor Appl Mech 46(6):739–746

    Google Scholar 

  40. Gao X, Ma H (2015) Topology optimization of continuum structures under buckling constraints. Comput Struct 157:142–152

    Google Scholar 

  41. Doan QH, Lee DK (2017) Optimum topology design of multi-material structures with non-spurious buckling constraints. Adv Eng Softw 114:110–120

    Google Scholar 

  42. Doan QH, Lee DK, Lee JH, Kang JW (2019) Design of buckling constrained multiphase material structures using continuum topology optimization. Meccanica 54:1179–1201

    MathSciNet  Google Scholar 

  43. Dunning PD, Ovtchinnikov E, Scott J, Kim HA (2016) Level-set topology optimization with many linear buckling constraints using an efficient and robust eigen solver. Int J Numer Methods Eng 107(12)

  44. Svanberg K (1987) The method of moving asymptotes-a new method for structural optimization. Int J Numer Methods Eng 24(2):359–373

    MathSciNet  MATH  Google Scholar 

  45. Olhoff N, Rasmussen SH (1977) On single and bimodal optimum buckling loads of clamped columns. Int J Numer Methods Eng 13(7):605–614

    MATH  Google Scholar 

  46. Radhika N, Teja K, Rahul K, Shivashankar A (2018) Fabrication of Cu-Sn-Ni /SiC FGM for automotive applications: investigation of its mechanical and tribological properties. Environ Sci Pollut Res 10:1705–1716

    Google Scholar 

  47. Paulino GH, Sutradhar A, Gray JL (2002) Boundary element methods for functionally graded materials. Bound Elem 4:1705–1716

    Google Scholar 

  48. Silva NCA, Paulino GH (2004) Topology optimization applied to the design of functionally graded material (FGM) structures. In: Proceedings of 21st international congress of theoretical and applied mechanics(ICTAM), pp 15–21

  49. Paulino GH, Silva NCA (2005) Design of functionally graded structures using topology optimization. J Appl Mech 492–493:435–440

    Google Scholar 

  50. Banh TT, Luu NG, Lee DK (2021) A non-homogeneous multi-material topology optimization approach for functionally graded structures with cracks. Compos Struct 273:114230

    Google Scholar 

  51. Li H, Gao L, Li H, Tong H (2020) Spatial-varying multi-phase infill design using density-based topology optimization. Comput Methods Appl Math 372:113354

    MathSciNet  MATH  Google Scholar 

  52. Zhou Y, Gao L, Li H (2022) Graded infill design within free-form surfaces by conformal mapping. Int J Mech Sci 224:107307

    Google Scholar 

Download references

Acknowledgements

This research was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2022R1A2C1003776).

Author information

Authors and Affiliations

  1. Department of Architectural Engineering, Sejong University, 209 Neungdong-ro, Gwangjin-gu, Seoul, 05006, Republic of Korea

    Nguyen Minh Ngoc & Dongkyu Lee

  2. Mechanical Engineering Institute, Vietnam Maritime University, Hai Phong City, Vietnam

    Van-Nam Hoang

Authors
  1. Nguyen Minh Ngoc
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Van-Nam Hoang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Dongkyu Lee
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Dongkyu Lee.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ngoc, N.M., Hoang, VN. & Lee, D. Concurrent topology optimization of coated structure for non-homogeneous materials under buckling criteria. Engineering with Computers 38, 5635–5656 (2022). https://doi.org/10.1007/s00366-022-01718-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-022-01718-2

Keywords