Skip to main content

Advertisement

Springer Nature Link
Log in

Modified nonlocal couple stress isogeometric approach for bending and free vibration analysis of functionally graded nanoplates

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

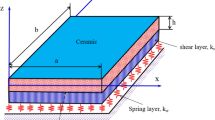
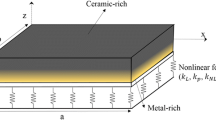
In this article, isogeometric analysis (IGA) based on the modified nonlocal couple stress theory (MNCST) is introduced to study bending and free vibration characteristics of functionally graded (FG) nanoplates placed on an elastic foundation (EF). The MNCST is a combination of nonlocal elasticity theory and modified couple stress theory to capture the small-size effects most accurately, hence this theory considers both softening and stiffening effects on responses of FG nanoplates. A higher order refined plate theory is adapted, because it satisfies parabolic distributions of transverse shear stresses across the nanoplate thickness and equals zero at the top and bottom surfaces without requiring shear correction factors. The governing equations are obtained using Hamilton's principle from which deduce the equations determining the natural frequency and displacement of the FG nanoplates. Several comparison studies are conducted to verify the proposed model with other results in the literature. Furthermore, the influence of nonlocal parameters, material length parameters, boundary conditions, material volume exponent on the bending, and free vibration response of FG nanoplates are fully studied.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig.1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data availability

The data used to support the findings of this study are included in the article.

References

  1. Vo TP, Thai H-T, Nguyen T-K, Maheri A, Lee J (2014) Finite element model for vibration and buckling of functionally graded sandwich beams based on a refined shear deformation theory. Eng Struct 64:12–22. https://doi.org/10.1016/j.engstruct.2014.01.029

    Article  Google Scholar 

  2. Asghari M, Ahmadian MT, Kahrobaiyan MH, Rahaeifard M (2010) On the size-dependent behavior of functionally graded micro-beams. Mater Des 31(5):2324–2329. https://doi.org/10.1016/j.matdes.2009.12.006

    Article  Google Scholar 

  3. Trinh LC, Vo TP, Osofero AI, Lee J (2016) Fundamental frequency analysis of functionally graded sandwich beams based on the state space approach. Compos Struct 156:263–275. https://doi.org/10.1016/j.compstruct.2015.11.010

    Article  Google Scholar 

  4. Vo TP, Thai H-T, Nguyen T-K, Inam F (2013) Static and vibration analysis of functionally graded beams using refined shear deformation theory. Meccanica 49(1):155–168. https://doi.org/10.1007/s11012-013-9780-1

    Article  MathSciNet  MATH  Google Scholar 

  5. Reddy JN (2000) Analysis of functionally graded plates. Int J Numer Methods Eng 47(1–3):663–684

    MATH  Google Scholar 

  6. Thai H-T, Vo TP (2013) A new sinusoidal shear deformation theory for bending, buckling, and vibration of functionally graded plates. Appl Math Model 37(5):3269–3281. https://doi.org/10.1016/j.apm.2012.08.008

    Article  MathSciNet  MATH  Google Scholar 

  7. Nguyen V-H, Nguyen T-K, Thai H-T, Vo TP (2014) A new inverse trigonometric shear deformation theory for isotropic and functionally graded sandwich plates. Compos B Eng 66:233–246. https://doi.org/10.1016/j.compositesb.2014.05.012

    Article  Google Scholar 

  8. Zenkour AM (2006) Generalized shear deformation theory for bending analysis of functionally graded plates. Appl Math Model 30(1):67–84. https://doi.org/10.1016/j.apm.2005.03.009

    Article  MATH  Google Scholar 

  9. Li S, Zheng S, Chen D (2020) Porosity-dependent isogeometric analysis of bi-directional functionally graded plates. Thin-Walled Struct 156:106999

    Google Scholar 

  10. Hosseini-Hashemi S, Fadaee M, Atashipour SR (2011) A new exact analytical approach for free vibration of Reissner-Mindlin functionally graded rectangular plates. Int J Mech Sci 53(1):11–22

    Google Scholar 

  11. Zhao X, Lee YY, Liew KM (2009) Free vibration analysis of functionally graded plates using the element-free kp-Ritz method. J Sound Vib 319(3–5):918–939

    Google Scholar 

  12. Nguyen-Xuan H, Tran LV, Nguyen-Thoi T, Vu-Do HC (2011) Analysis of functionally graded plates using an edge-based smoothed finite element method. Compos Struct 93(11):3019–3039

    Google Scholar 

  13. Chakraverty S, Pradhan K (2014) Free vibration of exponential functionally graded rectangular plates in thermal environment with general boundary conditions. Aero Sci Technol 36:132–156

    Google Scholar 

  14. Karamanlı A, Vo TP (2018) Size dependent bending analysis of two directional functionally graded microbeams via a quasi-3D theory and finite element method. Compos B Eng 144:171–183

    Google Scholar 

  15. Thai CH, Zenkour AM, Abdel-Wahab M, Nguyen-Xuan H (2016) A simple four-unknown shear and normal deformations theory for functionally graded isotropic and sandwich plates based on isogeometric analysis. Compos Struct 39:77–95

    Google Scholar 

  16. Tran TT, Pham QH, Nguyen-Thoi T (2021) Static and free vibration analyses of functionally graded porous variable-thickness plates using an edge-based smoothed finite element method. Defence Technol 17:971–986

    Google Scholar 

  17. Tran TT, Pham QH, Nguyen-Thoi T (2020) An edge-based smoothed finite element for free vibration analysis of functionally graded porous (FGP) plates on elastic foundation taking into mass (EFTIM). Math Probl Eng 2020:8278743

    MathSciNet  Google Scholar 

  18. Sobhy M (2015) A comprehensive study on FGM nanoplates embedded in an elastic medium. Compos Struct 134:966–980

    Google Scholar 

  19. Tran TT, Pham Q-H, Nguyen-Thoi T (2020) Dynamic analysis of functionally graded porous plates resting on elastic foundation taking into mass subjected to moving loads using an edge-based smoothed finite element method. Shock Vib 2020

  20. Nguyen P-C, Pham QH, Tran TT, Nguyen-Thoi T (2022) Effects of partially supported elastic foundation on free vibration of FGP plates using ES-MITC3 elements. Ain Shams Eng J 13:101615

    Google Scholar 

  21. Nguyen H-N, Canh TN, Thanh TT, Ke TV, Phan V-D, Thom DV (2019) Finite element modelling of a composite shell with shear connectors. Symmetry 11(4):527

    MATH  Google Scholar 

  22. Pham Q-H, Tran TT, Tran VK, Nguyen P-C, Nguyen-Thoi T, Zenkour AM , Bending and hygro-thermo-mechanical vibration analysis of a functionally graded porous sandwich nanoshell resting on elastic foundation. Mech Adv Mater Struct 1–21

  23. Tornabene F (2009) Free vibration analysis of functionally graded conical, cylindrical shell and annular plate structures with a four-parameter power-law distribution. Comput Methods Appl Mech Eng 198(3740):2911–2935. https://doi.org/10.1016/j.cma.2009.04.011

    Article  MATH  Google Scholar 

  24. Mantari JL (2015) Refined and generalized hybrid type quasi-3d shear deformation theory for the bending analysis of functionally graded shells. Compos B Eng 83:142–152. https://doi.org/10.1016/j.compositesb.2015.08.048

    Article  Google Scholar 

  25. Torabi J, Kiani Y, Eslami MR (2013) Linear thermal buckling analysis of truncated hybrid FGM conical shells. Compos B Eng 50:265–272. https://doi.org/10.1016/j.compositesb.2013.02.025

    Article  Google Scholar 

  26. Fu Y, Du H, Huang W, Zhang S, Hu M (2004) TiNi-based thin films in MEMS applications: a review. Sens Actuators A 112(23):395–408. https://doi.org/10.1016/j.sna.2004.02.019

    Article  Google Scholar 

  27. Baughman RH, Cui C, Zakhidov AA, Iqbal Z, Barisci JN, Spinks GM, Wallace GG, Mazzoldi A, Rossi DD, Rinzler AG, Jaschinski O, Roth S, Kertesz M (1999) Carbon nanotube actuators. Science 284(5418):1340–1344. https://doi.org/10.1126/science.284.5418.1340

    Article  Google Scholar 

  28. Lau K-T, Cheung H-Y, Lu J, Yin Y-S, Hui D, Li H-L (2008) Carbon nanotubes for space and bioengineering applications. J Comput Theor Nanosci 5(1):23–35. https://doi.org/10.1166/jctn.2008.003

    Article  Google Scholar 

  29. Liew KM, He XQ, Wong CH (2004) On the study of elastic and plastic properties of multi-walled carbon nanotubes under axial tension using molecular dynamics simulation. Acta Mater 52(9):2521–2527. https://doi.org/10.1016/j.actamat.2004.01.043

    Article  Google Scholar 

  30. Frankland SJV, Caglar A, Brenner DW, Griebel M (2002) Molecular simulation of the influence of chemical cross-links on the shear strength of carbon nanotube polymer interfaces. J Phys Chem B 106(12):3046–3048. https://doi.org/10.1021/jp015591+

    Article  Google Scholar 

  31. Fleck NA, Muller GM, Ashby MF, Hutchinson JW (1994) Strain gradient plasticity: theory and experiment. Acta Metall Mater 42(2):475–487. https://doi.org/10.1016/0956-7151(94)90502-9

    Article  Google Scholar 

  32. Stlken JS, Evans AG (1998) A microbend test method for measuring the plasticity length scale. Acta Mater 46(14):5109–5115. https://doi.org/10.1016/S1359-6454(98)00153-0

    Article  Google Scholar 

  33. Eringen AC (1972) Nonlocal polar elastic continua. Int J Eng Sci 10(1):1–16

    MathSciNet  MATH  Google Scholar 

  34. Pham Q-H, Nguyen P-C, Tran TT, Nguyen-Thoi T (2021) Free vibration analysis of nanoplates with auxetic honeycomb core using a new third-order finite element method and nonlocal elasticity theory. Engine with Comput 2021:1–19

    Google Scholar 

  35. Pham Q-H, Nguyen P-C, Tran TT (2022) Dynamic response of porous functionally graded sandwich nanoplates using nonlocal higher-order isogeometric analysis. Compos Struct 290:115565.

    Google Scholar 

  36. Fleck NA, Hutchinson JW (1993) A phenomenological theory for strain gradient effects in plasticity. J Mech Phys Solids 41(12):1825–1857

    MathSciNet  MATH  Google Scholar 

  37. Toupin RA (1962) Elastic materials with couple-stresses. Arch Ration Mech Anal 11(1):385–414

    MathSciNet  MATH  Google Scholar 

  38. Yang F, Chong ACM, Lam DCC, Tong P (2002) Couple stress based strain gradient theory for elasticity. Int J Solids Struct 39(10):2731–2743

    MATH  Google Scholar 

  39. Gao X-L, Zhang GY (2016) A non-classical Kirchhoff plate model incorporating microstructure, surface energy and foundation effects. Continuum Mech Thermodyn 28(1):195–213

    MathSciNet  MATH  Google Scholar 

  40. Reddy JN (2007) Nonlocal theories for bending, buckling and vibration of beams. Int J Eng Sci 45:288–307

    MATH  Google Scholar 

  41. Reddy JN (2010) Nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates. Int J Eng Sci 48(11):1507–1518

    MathSciNet  MATH  Google Scholar 

  42. Lu P, Zhang PQ, Lee HP, Wang CM, Reddy JN (2007) Non-local elastic plate theories. Proc. R. Soc. A 463:3225–3240

    MathSciNet  MATH  Google Scholar 

  43. Ahababaei R, Reddy JN (2009) Nonlocal third-order shear deformation plate theory with application to bending and vibration of plate. J Sound Vib 326(1–2):277–289

    Google Scholar 

  44. Satish N, Narendar S, Gopalakrishnan S (2012) Thermal vibration analysis of orthotropic nanoplate based on nonlocal continuum mechanics. Phys E 44(9):1950–1962

    Google Scholar 

  45. Malekzadeh P, Shojaee M (2013) Free vibration of nanoplates based on a nonlocal two-variable refined plate theory. Compos Struct 95:443–452

    Google Scholar 

  46. Shahidi AR, Anjomshoa A, Shahidi SH, Kamrani M (2013) Fundamental size dependent natural frequencies of non-uniform orthotropic nano scaled plates using nonlocal variational principle and finite element method. Appl Math Model 37:7047–7061

    MathSciNet  MATH  Google Scholar 

  47. Tran VK, Tran TT, Phung MV, Pham QH, Nguyen-Thoi T (2020) A finite element formulation and nonlocal theory for the static and free vibration analysis of the sandwich functionally graded nanoplates resting on elastic foundation. J Nanomater 2020:8786373

    Google Scholar 

  48. Doan TL, Le PB, Tran TT, Trai VK, Pham QH (2021) Free vibration analysis of functionally graded porous nano-plates with different shapes resting on elastic foundation. J Appl Comput Mech 7(3):1593–1605

    Google Scholar 

  49. Pham QH, Tran VK, Tran TT, Nguyen-Thoi T, Nguyen PC (2021) A nonlocal quasi-3D theory for thermal free vibration analysis of functionally graded material nanoplates resting on elastic foundation. Case Studies Therm Eng 26:101170

    Google Scholar 

  50. Pham QH, Tran TT, Tran VK, Nguyen PC, Nguyen-Thoi T (2021) Free vibration of functionally graded porous non-uniform thickness annular-nanoplates resting on elastic foundation using ES-MITC3 element. Alex Eng J 61(3):1788–1802

    Google Scholar 

  51. Tran VK, Pham QH, Nguyen-Thoi T (2022) A finite element formulation using four-unknown incorporating nonlocal theory for bending and free vibration analysis of functionally graded nanoplates resting on elastic medium foundations. Eng Comput 38:1465–1490

    Google Scholar 

  52. Mindlin RD, Tiersten HF (1962) Effects of couple-stresses in linear elasticity. Arch Ration Mech Anal 11(1):415–448

    MathSciNet  MATH  Google Scholar 

  53. Park SK, Gao X-L (2007) Variational formulation of a modified couple stress theory and its application to a simple shear problem. Zeitschrift fr angewandte Mathematik und Physik 59(5):904–917. https://doi.org/10.1007/s00033-006-6073-8

    Article  MathSciNet  MATH  Google Scholar 

  54. Ke L-L, Wang Y-S (2011) Size effect on dynamic stability of functionally graded microbeams based on a modified couple stress theory. Compos Struct 93(2):342–350

    Google Scholar 

  55. Roque CMC, Fidalgo DS, Ferreira AJM, Reddy JN (2013) A study of a microstructure-dependent composite laminated Timoshenko beam using a modified couple stress theory and a meshless method. Compos Struct 96:532–537

    Google Scholar 

  56. Thai H-T, Vo TP, Nguyen T-K, Lee J (2015) Size-dependent behavior of functionally graded sandwich microbeams based on the modified couple stress theory. Compos Struct 123:337–349

    Google Scholar 

  57. Tsiatas GC (2009) A new Kirchhoff plate model based on a modified couple stress theory. Int J Solids Struct 46(13):2757–2764

    MATH  Google Scholar 

  58. Yin L, Qian Q, Wang L, Xia W (2010) Vibration analysis of microscale plates based on modified couple stress theory. Acta Mech Solida Sin 23(5):386–393

    Google Scholar 

  59. Ma HM, Gao X-L, Reddy JN (2011) A non-classical Mindlin plate model based on a modified couple stress theory. Acta Mech 220:217–235

    MATH  Google Scholar 

  60. Reddy JN, Kim J (2012) A nonlinear modified couple stress-based third-order theory of functionally graded plates. Compos Struct 94(3):1128–1143

    Google Scholar 

  61. Reddy JN, Berry J (2012) Nonlinear theories of axisymmetric bending of functionally graded circular plates with modified couple stress. Compos Struct 94(12):3664–3668

    Google Scholar 

  62. Kim J, Reddy JN (2015) A general third-order theory of functionally graded plates with modified couple stress effect and the von karman nonlinearity: theory and finite element analysis. Acta Mech 226(9):2973–2998

    MathSciNet  MATH  Google Scholar 

  63. He L, Lou J, Zhang E, Wang Y, Bai Y (2015) A size-dependent four variable refined plate model for functionally graded microplates based on modified couple stress theory. Compos Struct 130:107–115

    Google Scholar 

  64. Thai H-T, Kim S-E (2013) A size-dependent functionally graded reddy plate model based on a modified couple stress theory. Compos B Eng 45(1):1636–1645

    Google Scholar 

  65. Thai CH, Ferreira AJM, Phung-Van P (2020) A nonlocal strain gradient isogeometric model for free vibration and bending analyses of functionally graded plates. Compos Struct 251:112634

    Google Scholar 

  66. Askes H, Aifantis EC (2011) Gradient elasticity in statics and dynamics: an overview of formulations, length scale identification procedures, finite element implementations and new results. Int J Solids Struct 48(13):1962–1990

    Google Scholar 

  67. Soldatos KP (1992) A transverse shear deformation theory for homogeneous monoclinic plates. Acta Mech 94(3):195–220

    MathSciNet  MATH  Google Scholar 

  68. Attia MA, Mahmoud FF (2016) Modeling and analysis of nanobeams based on nonlocal-couple stress elasticity and surface energy theories. Int J Mech Sci 105:126–134

    Google Scholar 

  69. Ebrahimi F, Barati MR, Civalek Ö (2020) Application of Chebyshev-Ritz method for static stability and vibration analysis of nonlocal microstructure-dependent nanostructures. Eng Comput 36:953–964

    Google Scholar 

  70. Ebrahimi F, Barati MR (2017) A modified nonlocal couple stress-based beam model for vibration analysis of higher-order FG nanobeams. Mech Adv Mater Struct 25(13):1121–1132

    Google Scholar 

  71. Miandoab EM, Pishkenari HN, Yousefi-Koma A, Hoorzad H (2014) Polysilicon nano-beam model based on modified couple stress and Eringen’s nonlocal elasticity theories. Phys E 63:223–228

    Google Scholar 

  72. Kumar H, Mukhopadhyay S (2022) Size-dependent thermoelastic damping analysis in nanobeam resonators based on Eringen’s nonlocal elasticity and modified couple stress theories. J Vib Control 2022:10775463211064689

    Google Scholar 

  73. Attar F, Khordad R, Zarif A, Modabberasl A (2021) Application of nonlocal modifed couple stress to study of functionally graded piezoelectric plates. Physica B 600:412623

    Google Scholar 

  74. Sourki R, Hosseini SA (2017) Coupling effects of nonlocal and modified couple stress theories incorporating surface energy on analytical transverse vibration of a weakened nanobeam. Eur Phys J Plus 132:184

    Google Scholar 

  75. Hughes TJR, Cottrell JA, Bazilevs Y (2005) Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput Methods Appl Mech Engrg 194(39–41):4135–4195

    MathSciNet  MATH  Google Scholar 

  76. Borden MJ, Scott MA, Evams JA, Hughes TJR (2011) Isogeometric finite element data structures based on Bezier extraction of NURBS. Int J Numer Methods Eng 87(1–5):15–47

    MATH  Google Scholar 

  77. Nguyen-Xuan H, Tran LV, Thai CH, Kulasegaram S, Bordas S (2014) Isogeometric analysis of functionally graded plates using a refined plate theory. Compos B Eng 64:222–234. https://doi.org/10.1016/j.compositesb.2014.04.001

    Article  Google Scholar 

  78. Vuong AV, Heinrich C, Simeon B (2010) ISOGAT: a 2d tutorial MATLAB code for isogeometric analysis. Comput Aided Geomet Des 27(8):644–655. https://doi.org/10.1016/j.cagd.2010.06.006

    Article  MathSciNet  MATH  Google Scholar 

  79. Lieu QX, Lee S, Kang J, Lee J (2018) Bending and free vibration analyses of in-plane bi- directional functionally graded plates with variable thickness using isogeometric analysis. Compos Struct 192:434–451

    Google Scholar 

  80. Lieu QX, Lee D, Kang J, Lee J (2018) NURBS-based modeling and analysis for free vibration and buckling problems of in-plane bi-directional functionally graded plates. Mech Adv Mater Struct 26:1064–1080

    Google Scholar 

  81. Phung-Van P, Abdel-Wahab M, Liew KM, Bordas SPA, Nguyen-Xuan H (2015) Isogeometric analysis of functionally graded carbon nanotube-reinforced composite plates using higher-order shear deformation theory. Compos Struct 123:137–149

    Google Scholar 

  82. Kiani Y (2018) Isogeometric large amplitude free vibration of graphene reinforced laminated plates in thermal environment using NURBS formulation. Comput Methods Appl Mech Eng 332:86–101

    MathSciNet  MATH  Google Scholar 

  83. Nguyen VP, Anitescu C, Bordas SPA, Rabczuk T (2015) Isogeometric analysis: an overview and computer implementation aspects. Math Comput Simulat 117:89–116

    MathSciNet  MATH  Google Scholar 

  84. Bischoff M, Echter R (2010) Numerical efficiency, locking and unlocking of NURBS finite elements. Comput Methods Appl Mech Eng 199(5–8):374–382

    MATH  Google Scholar 

  85. Nguyen HX, Nguyen TN, Abdel-Wahab M, Bordas SPA, Nguyen-Xuan H, Vo TP (2017) Isogeometric analysis for functionally graded microplates based on modified couple stress theory. Comput Methods Appl Mech Eng 313:904–940

    MATH  Google Scholar 

  86. Yang F, Chong ACM, Lam DCC, Tong P (2002) Couple stress based strain gradient theory for elasticity. Int J Solids Struct 39:2731–2743

    MATH  Google Scholar 

  87. Anjomshoa A, Shahidi AR, Hassani B, Jomehzadeh E (2014) Finite element buckling analysis of multi-layered graphene sheets on elastic substrate based on nonlocal elasticity theory. Appl Math Model 38:5934–5955

    MathSciNet  MATH  Google Scholar 

  88. Nguyen N-T, Hui D, Lee J, Nguyen-Xuan H (2015) An efficient computational approach for size-dependent analysis of functionally graded nanoplates. Comput Methods Appl Mech Eng. https://doi.org/10.1016/j.cma.2015.07.021

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge the financial support granted by the Scientific Research Fund of Ho Chi Minh City Open University for this project.

Author information

Authors and Affiliations

  1. Advanced Structural Engineering Laboratory, Department of Structural Engineering, Faculty of Civil Engineering, Ho Chi Minh City Open University, Ho Chi Minh City, Vietnam

    Quoc-Hoa Pham & Phu-Cuong Nguyen

  2. Faculty of Mechanical Engineering, Le Quy Don Technical University, Hanoi, Vietnam

    Van Ke Tran & Trung Thanh Tran

  3. Faculty of Civil Engineering, Ho Chi Minh City University of Technology (HCMUT), 268 Ly Thuong Kiet Street, District 10, Ho Chi Minh City, Vietnam

    Qui X. Lieu

  4. Vietnam National University Ho Chi Minh City (VNU-HCM), Linh Trung Ward, Thu Duc City, Ho Chi Minh City, Vietnam

    Qui X. Lieu

Authors
  1. Quoc-Hoa Pham
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Phu-Cuong Nguyen
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Van Ke Tran
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Qui X. Lieu
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Trung Thanh Tran
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Phu-Cuong Nguyen.

Ethics declarations

Conflicts of interest

The authors declare that there are no conflicts of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pham, QH., Nguyen, PC., Tran, V.K. et al. Modified nonlocal couple stress isogeometric approach for bending and free vibration analysis of functionally graded nanoplates. Engineering with Computers 39, 993–1018 (2023). https://doi.org/10.1007/s00366-022-01726-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-022-01726-2

Keywords