Skip to main content

Advertisement

SpringerLink
Log in

Highly efficient and fully decoupled BDF time-marching schemes with unconditional energy stabilities for the binary phase-field crystal models

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

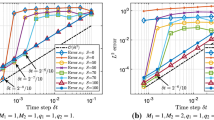
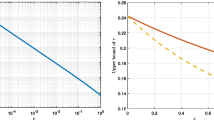
In this paper, we present totally decoupled, efficiently linear, and energy stable schemes for solving the binary phase-field crystal model. We introduce a new auxiliary variable to reformulate the model. Based on the backward Euler formula and the second-order backward difference formula (BDF2), we construct the first- and second-order time-accurate schemes, respectively. The modified energy not only can be calculated directly from the schemes but also satisfies the energy dissipation law. In each time step, we solve two linear elliptic equations with constant coefficients and other variables are explicitly computed. The fast Fourier transform (FFT) is adopted to accelerate the convergence. Thus, the computation is highly efficient. Various benchmark numerical experiments in 2D and 3D, such as the binary crystal growth, phase separation with vacancies, are performed to show the efficiency and performance of the proposed schemes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26

Similar content being viewed by others

References

  1. Elder KR, Katakowski M, Haataja M, Grant M (2002) Modeling elasticity in crystal growth. Phys Rev Lett 88:245701

    Google Scholar 

  2. Elder KR, Grant M (2002) Modeling elastic and plastic deformations in nonequilibrium processing using phase filed crystal. Phys Rev E 90:051605

    Google Scholar 

  3. Provatas N, Dantzig JA, Athreya B, Chan P, Stefanovic P, Goldenfeld N, Elder KR (2007) Using the phase-field crystal method in the multi-scale modeling of microstructure evolution. J Miner Metals Mater Soc 59(7):83–90

    Google Scholar 

  4. Mellenthin J, Karma A, Plapp M (2008) Phase-field crystal study of grain-boundary premelting. Phys Rev B 78:184110

    Google Scholar 

  5. Dehghan M, Mohammadi V (2016) The numerical simulation of the phase field crystal (PFC) and modified phase field crystal (MPFC) models via global and local meshless methods. Comput Methods Appl Mech Eng 298:453–484

    MathSciNet  MATH  Google Scholar 

  6. Li Y, Kim J (2017) An efficient and stable compact fourth-order finite difference scheme for the phase field crystal equation. Comput Methods Appl Mech Eng 319:194–216

    MathSciNet  MATH  Google Scholar 

  7. Lee HG, Kim J (2016) A simple and efficient finite difference method for the phase-field crystal equation on curved surfaces. Comput Methods Appl Mech Eng 307:32–43

    MathSciNet  MATH  Google Scholar 

  8. Yan Y, Chen W, Wang C, Wise SM (2018) A second-order energy stable BDF numerical scheme for the Cahn-Hilliard equation. Commun Comput Phys 23(2):572–602

    MathSciNet  MATH  Google Scholar 

  9. Li Y, Liu R, Xia Q, He C, Li Z (2022) First- and second-order unconditionally stable direct discretization methods for multi-component Cahn-Hilliard system on surfaces. J Comput Appl Math 401:113778

    MathSciNet  MATH  Google Scholar 

  10. Yang J, Kim J (2021) Linear, second-order accurate, and energy stable scheme for a ternary Cahn-Hilliard model by using lagrange multiplier approach. Acta Appl Math 172(1):1–20

    MathSciNet  MATH  Google Scholar 

  11. Li Q, Mei L (2021) Efficient, decoupled, and second-order unconditionally energy stable numerical schemes for the coupled Cahn-Hilliard system in copolymer/homopolymer mixtures. Comput Phys Commun 260:107290

    MathSciNet  MATH  Google Scholar 

  12. Zhang C, Ouyang J, Wang C, Wisec SM (2020) Numerical comparison of modified-energy stable SAV-type schemes and classical BDF methods on benchmark problems for the functionalized Cahn-Hilliard equation. J Comput Phys 423:109772

    MathSciNet  MATH  Google Scholar 

  13. Yang J, Tan Z, Kim J (2022) Linear and fully decoupled scheme for a hydrodynamics coupled phase-field surfactant system based on a multiple auxiliary variables approach. J Comput Phys 452:110909

    MathSciNet  MATH  Google Scholar 

  14. Li Q, Mei L (2021) Numerical Approximation of the Two-Component PFC Models for Binary Colloidal Crystals: Efficient, Decoupled, and Second-Order Unconditionally Energy Stable Schemes. J Sci Comput 88:60

    MathSciNet  MATH  Google Scholar 

  15. Yang J, Chen J, Tan Z (2022) Highly efficient variant of SAV approach for two-phase incompressible conservative Allen-Cahn fluids. Eng Comput. https://doi.org/10.1007/s00366-022-01618-5

    Article  Google Scholar 

  16. Yang J, Kim J (2022) Efficient and structure-preserving time-dependent auxiliary variable method for a conservative Allen-Cahn type surfactant system. Eng Comput. https://doi.org/10.1007/s00366-021-01583-5

    Article  Google Scholar 

  17. Wise SM, Wang C, Lowengrub JS (2009) An energy-stable and convergent finite-difference scheme for the phase field crystal equation. SIAM J Numer Anal 47:2269–2288

    MathSciNet  MATH  Google Scholar 

  18. Hu Z, Wise SM, Wang C, Lowengrub JS (2009) Stable and efficient finite-difference nonlinear-multigrid schemes for the phase field crystal equation. J Comput Phys 228:5323–5339

    MathSciNet  MATH  Google Scholar 

  19. Dong L, Feng W, Wang C, Wise SM, Zhang Z (2018) Convergence analysis and numerical implementation of a second order numerical scheme for the three-dimensional phase field crystal equation. Comput Math Appl 75(6):1912–1928

    MathSciNet  MATH  Google Scholar 

  20. Shin J, Lee HG, Lee JY (2016) First and second order numerical methods based on a new convex splitting for phase-field crystal equation. J Comput Phys 327:519–542

    MathSciNet  MATH  Google Scholar 

  21. Li Q, Mei L, Yang X, Li Y (2019) Efficient numerical schemes with unconditional energy stabilities for the modified phase field crystal equation. Adv Comput Math 1–30

  22. Liu Z, Li X (2020) Efficient modified stabilized invariant energy quadratization approaches for phase-field crystal equation. Numer Algorithms 85:107–132

    MathSciNet  MATH  Google Scholar 

  23. Wang L, Huang Y, Jiang K (2020) Error analysis of SAV finite element method to phase field crystal model. Numer Math Theor Methods Appl 13:372–399

    MathSciNet  MATH  Google Scholar 

  24. Pei S, Hou Y, You B (2019) A linearly second-order energy stable scheme for the phase field crystal model. Appl Numer Math 140:134–164

    MathSciNet  MATH  Google Scholar 

  25. Shin J, Lee HG, Lee JY (2020) Long-time simulation of the phase-field crystal equation using high-order energy-stable CSRK methods. Comput Methods Appl Mech Eng 364:112981

    MathSciNet  MATH  Google Scholar 

  26. Guan Z, Heinonen V, Lowengrub J, Wang C, Wise SM (2016) An energy stable, hexagonal finite difference scheme for the 2D phase field crystal amplitude equations. J Comput Phys 321:1026–1054

    MathSciNet  MATH  Google Scholar 

  27. Wang C, Wise SM (2011) An energy stable and convergent finite-difference scheme for the modified phase field crystal equation. SIAM J Numer Anal 49(3):945–969

    MathSciNet  MATH  Google Scholar 

  28. Cheng K, Wang C, Wise SM (2019) An energy stable BDF2 Fourier pseudo-spectral numerical scheme for the square phase field crystal equation. arXiv:1906.12255

  29. Elder KR, Provatas N, Berry J, Stefanovic P, Grant M (2007) Phase-field crystal modeling and classical density functional theory of freezing. Phys Rev B 75:064107

    Google Scholar 

  30. Elder KR, Huang ZF, Provatas N (2010) Amplitude expansion of the binary phase-field-crystal model. Phys Rev E 81:011602

    Google Scholar 

  31. Provatas N, Dantzig JA, Athreya B, Chan P, Stefanovic P, Goldenfeld N, Elder KR (2007) Using the phase-field crystal method in the multi-scale modeling of microstructure evolution. JOM 59:83

    Google Scholar 

  32. Tegze G, Bansel G, T\(\acute{\rm o}\)th GI, Pusztai T, Fan Z, Gr\(\acute{\rm a}\)n\(\acute{\rm a}\)sy L (2009) Advanced operator splitting-based semi-implicit spectral method to solve the binary phase-field crystal equations with variable coefficients. J Comput Phys 228(5):1612–1623

  33. Han S, Ye Q, Yang X (2021) Highly efficient and stable numerical algorithm for a two-component phase-field crystal model for binary alloys. J Comput Appl Math 390:113371

    MathSciNet  MATH  Google Scholar 

  34. Liu Z, Li X (2021) A highly efficient and accurate exponential semi-implicit scalar auxiliary variable (ESI-SAV) approach for dissipative system. J Comput Phys 447:110703

    MathSciNet  MATH  Google Scholar 

  35. Lee C, Kim H, Yoon S, Kim S, Lee D, Park J, Kwak S, Yang J, Wang J, Kim J (2021) An unconditionally stable scheme for the Allen-Cahn equation with high-order polynomial free energy. Nonlinear Sci Numer Simul 95:105658

    MathSciNet  MATH  Google Scholar 

  36. Yoon S, Jeong D, Lee C, Kim H, Kim S, Lee HG, Kim J (2020) Fourier-spectral method for the phase-field equations. Mathematics 8(8):1385

    Google Scholar 

  37. Lee K (2020) Chebyshev collocation method for the constant mobility Cahn-Hilliard equation in a square domain. Appl Math Comput 370:124931

    MathSciNet  MATH  Google Scholar 

  38. Berry J, Grant M (2011) Modeling multiple time scales during glass formation with phase-field crystals. Phys Rev Lett 106:175702

    Google Scholar 

  39. Elder KR, Provatas N, Berry J, Stefanovic P, Grant M (2007) Phase-field crystal modeling and classical density functional theory of freezing. Phys Rev B 75:064107

    Google Scholar 

  40. Elder KR (2004) Martin. Grant, Martin grant modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals. Phys Rev E 70:051605

  41. Zhu G, Kou J, Sun S, Yao J, Li A (2018) Decoupled, energy stable schemes for a phase-field surfactant model. Comput Phys Commun 233:67–77

    MathSciNet  MATH  Google Scholar 

  42. Yang J, Kim J (2021) Linear, second-order accurate, and energy stable scheme for a ternary Cahn-Hilliard model by using Lagrange multiplier approach. Acta Appl Math 172:10

    MathSciNet  MATH  Google Scholar 

  43. Yang J, Kim J (2021) A variant of stabilized-scalar auxiliary variable (S-SAV) approach for a modified phase-field surfactant model. Comput Phys Commun 261:107825

    MathSciNet  MATH  Google Scholar 

  44. Shen J, Xu J (2018) Convergence and error analysis for the scalar auxiliary variable (SAV) schemes to gradient flows. SIAM J Numer Anal 56(5):2895–2912

    MathSciNet  MATH  Google Scholar 

  45. Li X, Shen J, Rui H (2019) Energy stability and convergence of SAV block-centered finite difference method for gradient flows. Math Comput 88(319):2047–2068

    MathSciNet  MATH  Google Scholar 

  46. Li W, Chen W, Wang C, Yan Y, He R (2018) A second order energy stable linear scheme for a thin film model without slope selection. J Sci Comput 76(3):1905–1937

    MathSciNet  MATH  Google Scholar 

  47. Hwang Y, Lee C, Kwak S, Choi Y, Ham S, Kang S, Yang J, Kim J (2022) Benchmark problems for the numerical schemes of the phase-field equations. Discrete Dyn Nat Soc 2022:2751592

    MATH  Google Scholar 

  48. Lee HG, Kim J (2016) A simple and efficient finite difference method for the phase-field crystal equation on curved surfaces. Comput Methods Appl Mech Eng 307:32–43

    MathSciNet  MATH  Google Scholar 

  49. Hu Z, Wise SM, Wang C, Lowengrub JS (2009) Stable and efficient finite-difference nonlinear-multigrid schemes for the phase field crystal equation. J Comput Phys 228:5323–5339

    MathSciNet  MATH  Google Scholar 

  50. Yang J, Tan Z, Kim J (2021) High-order time-accurate, efficient, and structure-preserving numerical methods for the conservative Swift-Hohenberg model. Comput Math Appl 102:160–174

    MathSciNet  MATH  Google Scholar 

  51. Lee HG (2020) A new conservative Swift-Hohenberg equation and its mass conservative method. J Comput Appl Math 375:112815

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The work of Z. Tan is supported by the National Nature Science Foundation of China (11971502), Guangdong Natural Science Foundation (2022A1515010426)，Guangdong Province Key Laboratory of Computational Science at the Sun Yat-sen University (2020B1212060032), and Key-Area Research and Development Program of Guangdong Province (2021B0101190003). J. Yang is supported by the China Postdoctoral Science Foundation (No. 2022M713639).

Author information

Authors and Affiliations

  1. School of Computer Science and Engineering, Sun Yat-sen University, Guangzhou, 510275, China

    Jingwen Wu, Junxiang Yang & Zhijun Tan

  2. Guangdong Province Key Laboratory of Computational Science, Sun Yat-sen University, Guangzhou, 510275, China

    Zhijun Tan

Authors
  1. Jingwen Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Junxiang Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhijun Tan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhijun Tan.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, J., Yang, J. & Tan, Z. Highly efficient and fully decoupled BDF time-marching schemes with unconditional energy stabilities for the binary phase-field crystal models. Engineering with Computers 39, 3157–3181 (2023). https://doi.org/10.1007/s00366-022-01727-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-022-01727-1

Keywords

Search

Navigation