Skip to main content

Advertisement

Springer Nature Link
Log in

Stiffness mapping for early detection of breast cancer: combined force and displacement measurements

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

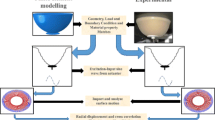
Early detection of breast cancer is crucial to patient survival. Our ultimate goal is to automate and refine the manual breast exam process using an electromechanical device that gently indents the tissue at multiple locations and measures the required indentation forces and the resulting displacements of the tissue surface. Our current experiments use a simplified electromechanical device and average-sized (180 cc) silicone breast phantoms to collect the force/displacement data. This data is used with finite element methods and a genetic algorithm to create a three-dimensional map of the stiffness inside the breast—unusually stiff regions are suspected tumors. We tested 14 tumor-free phantoms and 14 tumor-containing phantoms. Using a combination of 10% force data and 90% displacement data we could correctly classify all phantoms as tumor-containing or tumor-free, which was substantially more robust than either measurement modality alone. In addition, the approach is robust to errors in the stiffness assumed in the computations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

Notes

  1. A-341 from Factor II, Inc.

  2. Dow Xiameter PMX200 50 cs silicone fluid, Ellsworth Adhesives.

  3. Johnson’s Baby Powder, Original.

  4. HP 3D Scanner Pro S3 with dual cameras.

  5. Futek item FSH03871 LSB200 250g JR S-Beam Load Cell with FSH03927 External USB Output Kit.

  6. Again, the error for a tumor-free FE individual remains constant over all generations.

  7. It is 1/6 because there are 6 nodes in each surface element.

References

  1. (2020) American Cancer Society. http://www.cancer.org/

  2. (2020) National Cancer Institute, Division of Cancer Epidemiology and Genetics. https://dceg.cancer.gov/news-events/news/2017/breast-density

  3. (2020) Radiology Society of North America. http://www.radiologyinfo.org/

  4. Alam SK, Garra BS (2020) Tissue elasticity imaging. Elsevier

  5. Bamber J, Cosgrove D, Dietrich CF, Fromageau J, Bojunga J, Calliada F, Cantisani V, Correas JM, D’Onofrio M, Drakonaki EE, Fink M, Friedrich-Rust M, Gilja OH, Havre1 RF, Jenssen C, Klauser AS, Ohlinger R, Saftoiu A, Schaefer F, Sporea I, Piscaglia F, (2013) EFSUMB guidelines and recommendations on the clinical use of ultrasound elastography. Part 1: basic principles and technology. Ultraschall Med 34:169–184. https://doi.org/10.1055/s-0033-1335205

    Article  Google Scholar 

  6. Barr RG, Nakashima K, Amy D, Cosgrove D, Farrokh A, Schafer F, Bamber JC, Castera L, Choi BI, Chou YH, Dietrich CF, Ding H, Ferraioli G, Filice C, Friedrich-Rust M, Hall TJ, Nightingale KR, Palmeri ML, Shiina T, Suzuki S, Sporea I, Wilson S, Kudo M (2015) WFUMB guidelines and recommendations for clinical use of ultrasound elastography: part 2: breast. Ultrasound Med Biol 41(5):1148–1160. https://doi.org/10.1016/j.ultrasmedbio.2015.03.008

    Article  Google Scholar 

  7. Bayat M, Nabavizadeh A, Kumar V, Gregory A, Insana M, Alizad A, Fatemi M (2018) Automated in vivo sub-hertz analysis of viscoelasticity (save) for evaluation of breast lesions. IEEE Trans Biomed Eng 65(10):2237–2247. https://doi.org/10.1109/TBME.2017.2787679

    Article  Google Scholar 

  8. Bernal M, Chamming’s F, Couade M, Bercoff J, Tanter M, Gennisson JL (2016) In Vivo quantification of the nonlinear shear modulus in breast lesions: feasibility study. IEEE Trans Ultrasonics Ferroelectrics Frequency Control 63(1):101–109. https://doi.org/10.1109/TUFFC.2015.2503601

    Article  Google Scholar 

  9. Botterill T, Lotz T, Kashif A, Chase JG (2014) Reconstructing 3-d skin surface motion for the diet breast cancer screening system. IEEE Trans Med Imaging 33(4):1109–1118

    Article  Google Scholar 

  10. Clanahan JM, Reddy S, Broach RB, Rositch AF, Anderson BO, Wileyto EP, Englander BS, Brooks AD (2020) Clinical utility of a hand-held scanner for breast cancer early detection and patient triage. JCO Global Oncol 6:27–34. https://doi.org/10.1200/JGO.19.00205

    Article  Google Scholar 

  11. Doyley MM (2012) Model-based elastography: a survey of approaches to the inverse elasticity problem. Phys Med Biol 57:R35–R73

    Article  Google Scholar 

  12. Egorov V, Sarvazyan AP (2008) Mechanical imaging of the breast. IEEE Trans Med Imaging 27(9):1275–1287

    Article  Google Scholar 

  13. Egorov V, Tsyuryupa S, Kanilo S, Kogit M, Saravazyan A (2008) Soft tissue elastometer. Med Eng Phys 30:206–212

    Article  Google Scholar 

  14. Egorov V, Kearney T, Pollak SB, Rohatgi C, Sarvazyan N, Airapetian S, Browning S, Sarvazyan A (2009) Differentiation of benign and malignant breast lesions by mechanical imaging. Breast Cancer Res Treatment 118(1):67–80

    Article  Google Scholar 

  15. Egorov V, van Raalte H, Sarvazyan AP (2010) Vaginal tactile imaging. IEEE Trans Biomed Eng 57(7):1736–1744

    Article  Google Scholar 

  16. Goenezen S, Barbone P, Oberai AA (2011) Solution of the nonlinear elasticity imaging inverse problem: the incompressible case. Computer Methods Appl Mech Eng 200:1406–1420

    Article  MathSciNet  MATH  Google Scholar 

  17. Goenezen S, Luo P, Kim BJ, Kotecha M, Mei Y (2019) Mechanics based tomography using camera images. Mol Cell Biomech 16:46–48

    Article  Google Scholar 

  18. Goenezen S, Kim BJ, Kotecha M, Luo P, Hematiyan MR (2021) Mechanics based tomography (MBT): validation using experimental data. J Mech Phys Solids 146:104187. https://doi.org/10.1016/j.jmps.2020.104187

    Article  Google Scholar 

  19. Gokhale NH, Barbone PE, Oberai AA (2008) Solution of the nonlinear elasticity imaging inverse problem: the compressible case. Inverse Problems 24(045010):1–26

    MathSciNet  MATH  Google Scholar 

  20. Goswami S, Ahmed R, McAleavey MMDSA (2019) Nonlinear shear modulus estimation with bi-axial motion registered local strain. IEEE Trans Ultrasonics Ferroelectrics Frequency Control. https://doi.org/10.1109/TUFFC.2019.2919600

    Article  Google Scholar 

  21. Greenleaf JF, Fatemi M, Insana M (2003) Selected methods for imaging elastic properties of biological tissues. Ann Rev Biomed Eng 5:57–78

    Article  Google Scholar 

  22. Hann CE, Chase JG, Chen X, Berg C, Brown RG, Elliot RB (2009) Strobe imaging system for digital image-based elasto-tomography breast cancer screening. IEEE Trans Industr Electron 56(8):3195–3202

    Article  Google Scholar 

  23. Helvie MA, Carson PL, Saravazyan A, Thorson N, Egorov V, Roubidoux MA (2003) Mechanical imaging of the breast: a pilot trial. Ultrasound Med Biol 29(5S):S112

    Article  Google Scholar 

  24. Hii AJH, Hann CE, Chase JG, Van Houten E (2006) Fast normalized cross correlation for motion tracking using basis functions. Comput Methods Programs Biomed 82:144–156

    Article  Google Scholar 

  25. Hoerig C, Ghaboussi J, Insana MF (2019) Data-driven elasticity imaging using cartesian neural network constitutive models and the autoprogressive method. IEEE Trans Med Imaging 38(5):1150–1160. https://doi.org/10.1109/TMI.2018.2879495

    Article  Google Scholar 

  26. Kashif AS, Lotz TF, Heeren AMW, Chase JG (2013) Separate modal analysis for tumor detection with a digital image elasto tomography (diet) breast cancer screening system. Med Phys 40(11):113503:1-113503:8

    Article  Google Scholar 

  27. Kaufman CS, Son JS, Yered E, Sarvazyan A (2014) Clinical studies of palpation imaging of the breast on over 1000 patients. 2014 San Antonio Breast Cancer Symposium P1-02-09

  28. Kearney TJ, Airpetian A, Sarvazyan A (2004) Tactile breast imaging to increase the sensitivity of breast examination. J Clin Oncol 22(14S):1037

    Article  Google Scholar 

  29. Krouskop TA, Wheeler TM, Kallel F, Garra BS, Hall T (1998) Elastic moduli of breast and prostate tissues under compression. Ultrasonic Imaging 20:260–274

    Article  Google Scholar 

  30. Li GY, Cao Y (2017) Mechanics of ultrasound elasticity. Proc R Soc A https://doi.org/0.1098/rspa.2016.0841

  31. Loughry CW, Sheffer DB, Price TE, Lackney MJ, Bartfai RG, Morek WM (1986) Breast volume measurement of 248 women using biostereometric analysis. Plast Reconstr Surg 80(4):553–558

    Article  Google Scholar 

  32. Loughry CW, Sheffer DB, Price TE, Einsporn RL, Bartfai RG, Morek WM, Meli NM (1989) Breast volume measurement of 598 women using biostereometric analysis. Ann Plast Surg 22(5):380–385

    Article  Google Scholar 

  33. Luo P, Mei Y, Kotecha M, Abbasszadehrad A, Rabke S, Garner G, Goenezen S (2018) Characterization of the stiffness distribution in two and three dimensions using boundary deformations: A preliminary study. MRS Communicationa 8:893–902. https://doi.org/10.1557/mrc.2018.98

    Article  Google Scholar 

  34. Mehrabian H, Campbell G, Samani A (2010) A constrained reconstruction technique of hyperelasticity parameters for breast cancer assessment. Phys Med Biol 55:7489–7508

    Article  Google Scholar 

  35. Mei Y, Fulmer R, Raja V, Wang S, Goenezen S (2016) Estimating the non-homogeneous elastic modulus distribution from surface deformations. Int J Solids Struct 83:73–80. https://doi.org/10.1016/j.ijsolstr.2016.01.001

    Article  Google Scholar 

  36. Mei Y, Wang S, Shen X, Rabke S, Goenezen S (2017) Mechanics based tomography: a preliminary feasibility study. Sensors. https://doi.org/10.3390/s17051075

    Article  Google Scholar 

  37. Mei Y, Wang S, Shen X, Rabke S, Goenezen S (2018) Erratum: Mechanics based tomography: a preliminary feasibility study. Sensors. https://doi.org/10.3390/s18020384

    Article  Google Scholar 

  38. Oberai AA, Gokhale NH, Goenezen S, Barbone PE, Hall TJ, Sommer AM, Jiang J (2009) Linear and nonlinear elasticity imaging of soft tissue in vivo: demonstration of feasibility. Phys Med Biol 54:1191–1207

    Article  Google Scholar 

  39. O’Hagan JJ, Samani A (2008) Measurement of the hyperelastic properties of tissue slices with tumour inclusion. Phys Med Biol 53:7087–7106

    Article  Google Scholar 

  40. O’Hagan JJ, Samani A (2009) Measurement of the hyperelastic properties of 44 pathological ex vivo breast tissue samples. Phys Med Biol 54:2257–2569

    Google Scholar 

  41. Olson LG, Throne RD, Nolte AJ, Crump A, Griffin K, Han T, Iovanac N, Janssen T, Jones M, Ling X, Samp M (2019) An inverse problem approach to stiffness mapping for early detection of breast cancer: tissue phantom experiments. Inverse Problems Sci Eng 27(7):1006–1037. https://doi.org/10.1080/17415977.2018.1538367

    Article  Google Scholar 

  42. Olson LG, Throne RD, Rusnak EI, Gannon JP (2021) Force-based stiffness mapping for early detection of breast cancer. Inverse Problems Sci Eng. https://doi.org/10.1080/17415977.2021.1912036

    Article  MathSciNet  MATH  Google Scholar 

  43. Parker KJ, Doyley MM, Rubens DJ (2011) Imaging the elastic properties of tissue: the 20 year perspective. Phys Med Biol 56:1–29

    Article  Google Scholar 

  44. Patel D, Tibrewala R, Vega A, Dong L, Hugenberg N, Oberai AA (2019) Circumventing the solution of inverse problems in mechanics through deep learning: application to elasticity imaging. Comput Methods Appl Mech Eng 353:448–466. https://doi.org/10.1016/j.cma.2019.04.045

    Article  MathSciNet  MATH  Google Scholar 

  45. Peters A, Milsant A, Rouze J, Ray L, Chase JG, Van Houten E (2004) Digital image-based elasto-tomography: proof of concept studies for surface based mechanical property reconstruction. JOSE Int J 47(4):1117–1123

    Google Scholar 

  46. Peters A, Wortmann S, Elliott R, Staiger M, Chase JG, Van Houten E (2005) Digital image-based elasto-tomography: first experiments in surface based mechanical property estimation of gelatine phantoms. JOSE Int J 48(4):562–569

    Google Scholar 

  47. Peters A, Uwe-Berger H, Chase JG, Van Houten EEW (2006) Digital image-based elasto-tomography: non-linear mechanical property reconstruction of homogeneous gelatine phantoms. Int J Info Syst Sci 2(4):512–521

    MathSciNet  MATH  Google Scholar 

  48. Peters A, Chase JG, Van Houten EEW (2008) Digital image elasto-tomography: combinatorial and hybrid optimization algorithms for shape-based elastic property reconstruction. IEEE Trans Biomed Eng 55(11):2575–2583

    Article  Google Scholar 

  49. Peters A, Chase JG, Van Houten EEW (2009) Estimating elasticity in heterogeneous phantoms using digital image elasto-tomography. Med Biol Eng Comput 47:67–76

    Article  Google Scholar 

  50. Peterson J (2017) Introduction to suretouch for clinicians. https://sureincus/physician-introduction-1/

  51. van Raalte H, Egorov V (2015) Characterizing female pelvic floor conditions by tactile imaging. Int Urogynecol J 26:607–609

    Article  Google Scholar 

  52. Ries LAG, Young JL, Keel GE, Eisner MP, Lin YD, Horner MJ (eds) (2007) SEER Survival Monograph: Cancer Survival Among Adults: US SEER Program, 1988-2001, Patient and Tumor Characteristics. National Cancer Institute, SEER Program, NIH Pub. No. 07-6215, http://seer.cancer.gov/publications/survival/

  53. Samani A, Plewes D (2007) An inverse problem solution for measuring the elastic modulus of intact ex vivo breast tissue tumours. Phys Med Biol 52:1247–1260

    Article  Google Scholar 

  54. Samani A, Zubovits J, Plewes D (2007) Elastic moduli of normal and pathological human breast tissues: an inversion-technique-based investigation of 169 samples. Phys Med Biol 52:1565–1576

    Article  Google Scholar 

  55. Sarvazyan A, Egorov V (2012) Mechanical imaging - a technology for 3-d visualization and characterization of soft tissue abnormalities: a review. Curr Med Imaging Rev 8(1):64–73

    Article  Google Scholar 

  56. Seidl DT, Oberai AA, Barbone PE (2019) The coupled adjoint-state equation in forward and inverse linear elasticity: incompressible plane stress. Comput Methods Appl Mech Eng. https://doi.org/10.1016/j.cma.2019.112588

    Article  MathSciNet  MATH  Google Scholar 

  57. Shiina T, Nightingale KR, Palmeri ML, Hall TJ, Bamber JC, Barr RG, Castera L, Choi BI, Chou YH, Cosgrove D, Dietrich CF, Ding H, Amy D, Farrokh A, Ferraioli G, Filice C, Friedrich-Rust M, Nakashima K, Schafer F, Sporea I, Suzuki S, Wilson S, Kudo M (2015) WFUMB guidelines and recommendations for clinical use of ultrasound elastography: Part 1: basic principles and terminology. Ultrasound Med Biol 41(5):1126–1147. https://doi.org/10.1016/j.ultrasmedbio.2015.03.009

    Article  Google Scholar 

  58. Szewczyk ST, Shih WY, Shih WH (2006) Palpationlike soft-material elastic modulus measurement using piezoelectric cantilevers. Rev Scientific Instruments 77(044302):1–8

    Google Scholar 

  59. Săftoiu A, Gilja OH, Sidhu PS, Dietrich CF, Cantisani V, Amy D, Bachmann-Nielsen M, Bob F, Bojunga J, Brock M, Calliada F, Clevert DA, Correas JM, D’Onofrio M, Ewertsen C, Farrokh A, Fodor D, Fusaroli P, Havre RF, Hocke M, Ignee A, Jenssen C, Klauser AS, Kollmann C, Radzina M, Ramnarine KV, Sconfienza LM, Solomon C, Sporea I, Ṣtefănescu H, Tanter M, Vilmann P, (2019) The EFSUMB guidelines and recommendations for the clinical practice of elastography in non-hepatic applications: Update 2018. Ultraschall Med 40:425–453. https://doi.org/10.1055/a-0838-9937

    Article  Google Scholar 

  60. Xu X, Gifford-Hollingsworth C, Sensenig R, Shih WH, Shih WY, Brooks AD (2013) Breast tumor detection using piezoelectric fingers: first clinical report. J Am Coll Surg 216(6):1168–1173

    Article  Google Scholar 

  61. Xu X, Chung Y, Brooks AD, Shih WH, Shih WY (2016) Development of arry piezoelectric fingers towards in-vivo breast tumor detection. Rev Scientific Instruments 87:124301

    Article  Google Scholar 

  62. Yegingil H, Shih WY, Shih WH (2007) All-electrical indentation shear modulus and elastic modulus measurement using a piezoelectric cantilever with a tip. J Appl Phys 101(054510):1–10

    Google Scholar 

  63. Yegingil H, Shih WY, Shih WH (2007) Probing elastic tissue modulus and depth of bottom-supported inclusions in model tissues using piezoelectric cantilevers. Rev Scientific Instruments 78(115101):1–6

    Google Scholar 

  64. Yegingil H, Shih WY, Shih WH (2010) Probing model tumor interfacial properties using piezoelectric cantilevers. Rev Scientific Instruments 81(095104):1–9

    Google Scholar 

  65. Zhou C, Chase JG, Ismail H, Signal MK, Haggers M, Rodgers GW, Pretty C (2018) Silicone phantom validation of breast cancer tumor detection using nomical stiffness identification in digital imaging elasto-tomography. Biomed Signal Process Control 39:435–447. https://doi.org/10.1016/j.gspc.2017.08.022

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by generous contributions to the Lawrence J. Giacoletto endowment. Computing support was provided by the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562. Resources were obtained through the Texas Advanced Computing Center (TACC) at the University of Texas at Austin.

Author information

Authors and Affiliations

  1. Mechanical Engineering, Rose-Hulman Institute of Technology, Terre Haute, IN, 47802, USA

    Lorraine G. Olson

  2. Electrical Engineering, Rose-Hulman Institute of Technology, Terre Haute, IN, 47802, USA

    Robert D. Throne

Authors
  1. Lorraine G. Olson
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Robert D. Throne
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Lorraine G. Olson.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was supported by generous contributions to the Lawrence J. Giacoletto endowment. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562. Resources were obtained through the Texas Advanced Computing Center at the University of Texas at Austin.

Appendices

A displacement data processing

There are two phases to processing the displacement data so that it can be used as part of an error norm comparing finite element normal displacements to experimentally measured displacements: generating finite element normal displacements and converting experimentally measured STL files to corresponding normal displacements.

1.1 A.1 Finite element normal displacements and nodal areas

Let us suppose that we have a finite element mesh such as that shown in the stiffness map in Fig. 1, which is typical for our phantoms. Notice that some elements are small and some elements are large. If we compute the forward solution for an indentation site we will have the force required to impose that indentation along with the x, y, z displacements of the surface nodes. While each element has a well-defined normal direction the nodes do not have a normal as such—they are connected to several elements each of which has a different normal and a different size. In addition, the elements were created by processing an STL of the geometry and this sometimes introduces small peaks that result in widely varying normals in a small region.

To address these issues, we create a transformation matrix that takes the x, y, z displacements at the nodes and converts it into smoothed normal displacements at the nodes:

  1. 1.

    We find the normal to each surface element and also calculate its area. The elements are straight-sided 6-node elements so the normal and area are well-defined.

  2. 2.

    For each node on the surface we find all of the elements to which it is attached.

  3. 3.

    The normal for this node is the area-weighted average of the elements to which it is attached.

  4. 4.

    For each surface node, we replace its normal with the area-weighted average of the normals of all the nodes within a 5 mm radius

  5. 5.

    Finally we use these smoothed normals to create a matrix that transforms the x, y, z nodal displacements to normal nodal displacements

We also need to associate an area with each node in the cost calculation for the displacements—the area for each node is taken to be 1/6 of the sum of the areas of the elements to which it is attachedFootnote 7.

1.2 A.2 Processing the STL files

The STL file processing is repeated independently for each indentation site. Recall from Section 4 that we have two “before indentation” STL files (STL1 and STL2) and two “after indentation” STL files (STL3 and STL4). An STL file consists of triangles and vertices, and for our purposes we are only interested in the vertices which we treat as a cloud of surface xyz data points. We need to turn this cloud of points into normal nodal displacements for comparison with the finite element results. We also need to mark the nodes where there is no data. Figure 18 shows a typical cloud of points from a single STL.

Fig. 18
figure 18

Point cloud from a single STL scan file. (Approximately 450K points. The keyhole is missing data due to the indenter blocking the camera)

Full size image

We rotate and translate the four STL files into the same coordinate system that was used to generate the finite element mesh. This is straightforward.

For each STL file, for each finite element node:

  1. 1.

    Find all of the points in the STL file which are within 2 mm of the smoothed normal vector through the node.

  2. 2.

    If there are at least 10 points, mark that node as having “good” data. (Otherwise it is marked “bad” and not used in the cost calculation.)

  3. 3.

    Average the xyz location of those near points.

  4. 4.

    Find the normal distance from the finite element node to the average xyz location using the smoothed normals.

  5. 5.

    This is the normal distance from the node to the cloud.

Each STL file then produces a set of nodal normal distances and a preliminary list of nodes with good data.

We create an overall list of nodes with good data for this indenter which includes only nodes which have good data from all four STL files. If the difference between the nodal normal distances from the two precompression scans (STL1 and STL2) differ by more than 0.1 mm that node is also marked as bad. Similarly, if the difference between the nodal normal distances for the two indentation scans (STL3 and STL4) differ by more than 0.1 mm that node is marked as bad.

Next we create the final nodal normal displacement and list of nodes with good data by combining the nodal normal distance information from the four scans:

  1. 1.

    Average the normal nodal distance data for the two precompression scans.

  2. 2.

    Average the normal nodal distance data for the two indentation scans.

  3. 3.

    The nodal normal displacement is the difference of the indentation average normal nodal distance and the precompression average normal nodal distance.

  4. 4.

    If the nodal normal displacement at any node is more than 0.4 mm different than the average value of all of its neighbor nodes (within a radius of 2.5 mm) mark that node as bad.

This gives us (for one indentation site) a set of nodal normal displacements and a list of which nodes have good data. The normal displacements can be plotted as shown earlier in Figure 5.

B Additional details on genetic algorithm and computational costs

Here we briefly summarize some additional details on the genetic algorithm and it’s computational cost which may be of particular interest. Complete details about the genetic algorithm are available in our earlier papers. [41, 42].

1.1 B.1 Genetic algorithm details

The genetic algorithm individuals are completely defined by a chromosome which records whether the tissue in each clump is healthy or tumor tissue.

The 288 individuals in the first generation are chosen carefully to speed convergence and to help avoid falling into local minima. The first generation always includes one tumor-free individual. This choice ensures that a tumor-free result is always considered. The first generation also includes 144 individuals which have exactly one tumor clump each. This choice ensures that tumors throughout the tissue are considered. The remaining 143 individuals are generated by randomly assigning tumor or healthy tissue properties to each clump in the individual (equal likelihood of tumor or healthy). This choice ensures that a wide variety of tumor sizes is considered.

We evaluate the cost associated with each of the 288 individuals. The best 16 individuals (16 with lowest cost) are taken as “parents” for the next generation. Parents are retained for the next generation and then mated in pairs. For each pair of parents we generate 17 children. To generate a “child” we compare the genes on the chromosomes for the two parents: if the parents have the same gene (healthy or tumor) in a given location then the child has that gene; if the parents have different genes then the child has an even (random) chance for healthy or tumor tissue. Once all the children are created we choose a random number of children to receive mutations and on those children we switch a random number of genes. These mutations also help to avoid falling into a local minimum. The resulting population of 16 parents and 272 children are used for the next generation.

1.2 B.2 Computational costs

We are using Stampede 2 at the Texas Advanced Computing Center at University of Texas at Austin. Our code runs on 6 nodes with 48 processes per node (total 288 processes). The wall clock time for a full inverse to compute the stiffness map for one experiment is approximately 2 hours. We anticipate that algorithmic enhancements and hardware computing advancements will reduce this time in the future. The run time is essentially unchanged whether our cost function uses forces or displacements or their combination—the majority of the computation time is spent in solving the forward finite element problem which intrinsically produces both force and displacement information.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Olson, L.G., Throne, R.D. Stiffness mapping for early detection of breast cancer: combined force and displacement measurements. Engineering with Computers 38, 4023–4041 (2022). https://doi.org/10.1007/s00366-022-01741-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-022-01741-3

Keywords