Abstract
When considering mesh quality improvement and optimization via node movement, a particularly important goal is to attempt to improve the worst quality in the mesh when that quality is unacceptable. Standard mesh optimization methods often do not address worst case quality and can make it worse. Three fundamental methods for addressing worst case quality in mesh optimization by node movement have appeared in the literature: (1) a shifted barrier approach by Barrera et. al. (Math Comput Simul 46(2):87–102, 1998), (2) a pseudo-barrier approach by Escobar et. al. (Comput Methods Appl Mech Eng 192:2775–2787, 2000), and (3) another barrier approach by Garanzha et. al. (In: IMR 2021-29th international meshing roundtable, 2021). The first two result in ‘simultaneous untangle-optimizers’ while the last addresses worst case quality in terms of the maximum value of the optimization metric. In terms of mesh optimization within the Target Matrix Optimization Paradigm (TMOP), worst case quality is defined by two quantities: the maximum value of the optimization metric (\(\max \mu\)) and the minimum value of the local volume (\(\min \tau\)), both computed over the mesh sample points. In the present paper we show that the methods by the three authors cited above can be applied to the TMOP metrics and used on both linear and high-order element meshes. Unfortunately, the first two methods increase \(\max \tau\) but do not address \(\max \mu\). The third method addresses \(\max \mu\), but fails to address \(\min \tau\). Using a composition of functions approach, the present work creates new compound metrics that simultaneously increase \(\min \tau\) and decrease \(\max \mu\). This goal can also be accomplished by a two-stage optimization procedure in which the first stage untangles the initial mesh and the second stage decreases \(\max \mu\). Although none of these methods provide a guarantee that the worst case quality will be improved to the point that the quality becomes acceptable, it is shown by numerical examples that they can be very effective.













Similar content being viewed by others
Notes
Some simple theoretical tests exist for elements such as triangular or quadrilateral elements with linear maps.
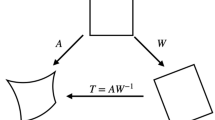
The index k indicates a particular TMOP metric and \(T = A W^{-1}\), with A the mesh Jacobian at a sample point and W the corresponding target matrix.
Our optimization code terminates when the maximum nodal distance-moved over the sample points is less than an input tolerance, tol. Thus, the code does not terminate when \(\min \tau\) becomes positive, nor should it with the SUO methods.
Since in TMOP the word ‘composite’ is reserved for metrics which have the form \(\mu = (1-\gamma ) \mu _a + \gamma \, \mu _b\), we shall call metrics formed by the composition of functions ‘compound’ metrics.
References
Barrera-Sanchez P, Tinoco-Ruiz J (1998) Smooth and convex grid generation over general plane regions. Math Comput Simul 46:87–102 (H)
Brackbill J, Saltzman J (1981) Adaptive zoning for singular problems in two dimensions. J Comput Phys 46:342–368
Brewer M, Freitag L, Knupp P, Leurent T, Melander D (2003) The Mesquite mesh quality improvement toolkit. In: Proceedings of the 12th intl. meshing roundtable, Sandia National Laboratories, pp 239–250
Castillo J (1991) A discrete variational grid generation method. SIAM J Sci Comput 12:454–468
Delanaye M, Hirsch C, Kovalev K (2003) Untangling and optimization of unstructured hexahedral meshes. Comput Math Math Phys 43:807–814
Dobrev V, Knupp P, Kolev T, Mittal K, Tomov V (2019) The target-matrix optimization paradigm for high-order meshes. SIAM J Sci Comput 41(1):B50–B68
Dvinsky A (1991) Adaptive grid generation from harmonic maps on Riemannian manifolds. J Comput Phys 95(2):450–476
Escobar J, Rodriguez E, Montenegro R, Montero G, Gonzalez-Yuste J (2003) Simultaneous untangling and smoothing of tetrahedral meshes. Comput Methods Appl Mech Eng 192:2775–2787
Freitag L (2001) Local optimization-based untangling algorithms for quadrilateral meshes. In: Proceedings of the 10th intl. meshing roundtable, Sandia National Laboratories, pp 397–406
Freitag L, Plassman P (2000) Local optimization-based simplicial mesh untangling and improvement. Int J Numer Methods Eng 49:109–125
Garanzha V, Kudryavtseva L, Utyuzhnikov S (2014) Variational method for untangling and optimization of spatial meshes. J Comput Appl Math 269:24–41
Garanzha V, Kaporin I, Kudryavtseva L, Protais F, Ray N, Sokolov D (2021) On local invertibility and quality of free-boundary deformations. In: International meshing roundtable
Gargallo-Peiro A, Roca X, Sarrate J (2014) A surface mesh smoothing and untangling method independent of the CAD parameterization. Comput Mech 53(4):587–609
Huang W, Russell R (2011) Adaptive moving meshes. In: Applied mathematical sciences series, vol 174. Springer, New York
Ivanenko S (1999) Harmonic mappings. Handbook of grid generation. CRC Press, Boca Raton
Knupp P (2001) Hexahedral and tetrahedral mesh untangling. Eng Comput 17(3):261–268
Knupp P (2008) Remarks on mesh quality. In: AIAA 2008-933, proceedings 46th AIAA aerospace sciences meeting
Knupp P (2012) Introducing the Target Matrix Paradigm for mesh optimization via node movement. Eng Comput 28(4):419–429
Knupp P (2019) Target formulation and construction in mesh quality improvement, LLNL-TR-795097. Lawrence Livermore National Laboratory, Livermore, p 94. https://www.osti.gov/biblio/1571722
Knupp P (2020) Metric type in the target-matrix mesh optimization paradigm, LLNL-TR-817490. Lawrence Livermore National Laboratory, Livermore. https://www.osti.gov/biblio/1782521-metric-type-target-matrix-mesh-optimization-paradigm
Liseikin V (1999) Grid Generation Methods. Springer, Berlin
Lopez E, Nigro N, Storti M (2008) Simultaneous untangling and smoothing of moving grids. Int J Numer Methods Eng 76:994–1019
Remacle J, Toulorge T, Lambrechts J (2013) Robust untangling of curvilinear meshes. In: Proceedings of the 21st intl. meshing roundtable. Springer, Berlin, pp 71–83
Steinberg S, Roache P (1986) Variational grid generation. Num Methods PDEs 2:71–96
Toulorge T, Geuzaine C, Remacle J, Lambrechts J (2013) Robust untangling of curvilinear meshes. J Comput Phys 254:8–26
Thompson J, Thames F, Mastin C (1974) Automatic numerical grid generation of boundary-fitted curvilinear coordinates for field containing any number of arbitrary two-dimensional bodies. J Comput Phys 15:299–319
Vachal P, Garimella R, Shashkov M (2004) Untangling of 2D meshes in ALE simulations. J Comput Phys 196:627–644
Winslow A (1967) Numerical solution of the quasilinear Poisson equations in a non-uniform triangle mesh. J Comput Phys 2:149–172
Zhang Y, Bajaj C, Xu G (2009) Surface smoothing and quality improvement of quadrilateral/hexahedral meshes with geometric flow. J Commun Num Methods Eng 25(1):1–18
Acknowledgements
The author would like to thank members of the ETHOS team: Veselin Dobrev, Tzanio Kolev, Ketan Mittal, and Vladimir Tomov.
Funding
Support provided by the ETHOS project, LLNL Subcontract B648806.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
There are no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Knupp, P. Worst case mesh quality in the target matrix optimization paradigm. Engineering with Computers 38, 5695–5711 (2022). https://doi.org/10.1007/s00366-022-01753-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00366-022-01753-z