Weak form of bond-associated peridynamic differential operator for solving differential equations

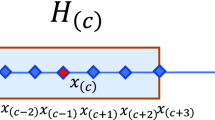
Abstract

In this paper, the weak form of bond-associated peridynamic differential operator is proposed to solve differential equations. The presented method inherits the advantages of the original peridynamic differential operator and enables directly and efficiently to determine the nonlocal weak form for local differential equations and obtain the corresponding symmetrical tangent stiffness matrix in the smaller size using variational principles. The concept of bond-associated family is introduced to suppress the numerical oscillation and zero-energy modes in this study. Several typical elasticity problems, taken as examples, are presented to show the application and capabilities of this method. The accuracy, convergence, and stability of the proposed method are demonstrated by seven numerical examples including linear and nonlinear, steady and transient state problems, and eigenvalue problems in 1D, 2D, and 3D cases.

Appendix

The bond-associated nonlocal divergence of a vector function u and its discrete form can be expressed through Eq. (6) as

$$\begin{gathered} \left( {\nabla \cdot {\mathbf{u}}} \right)_{{{\varvec{\upxi}}}} = \int_{{H_{{{\varvec{\upxi}}}} }} {{\mathbf{g}}_{{{\varvec{\upxi}}}} ({\overline{\mathbf{\xi }}}) \cdot \left( {{\mathbf{u}}_{{{\mathbf{x^{\prime\prime}}}}} - {\mathbf{u}}_{{\mathbf{x}}} } \right)dV_{{{\mathbf{x^{\prime\prime}}}}} } \hfill \\ \left( {\nabla \cdot {\mathbf{u}}} \right)_{[j](k)} = \sum\limits_{i = 1}^{{N_{[j](k)} }} {{\mathbf{g}}_{{\{ i\} [j](k)}} \cdot \left( {{\mathbf{u}}_{{\{ i\} }} - {\mathbf{u}}_{(k)} } \right)V_{{\{ i\} }} } . \hfill \\ \end{gathered}$$

(A.1)

The variation of $\left( {\nabla \cdot {\mathbf{u}}} \right)_{{{\varvec{\upxi}}}}$ and its discrete form can be obtained from Eq. (A.1) as

$$\begin{gathered} {\updelta }\left( {\nabla \cdot {\mathbf{u}}} \right)_{{{\varvec{\upxi}}}} = \int_{{H_{{{\varvec{\upxi}}}} }} {{\mathbf{g}}_{{{\varvec{\upxi}}}} ({\overline{\mathbf{\xi }}}) \cdot \left( {{\updelta }{\mathbf{u}}_{{{\mathbf{x^{\prime\prime}}}}} - {\updelta }{\mathbf{u}}_{{\mathbf{x}}} } \right)dV_{{{\mathbf{x^{\prime\prime}}}}} } \hfill \\ {\updelta }\left( {\nabla \cdot {\mathbf{u}}} \right)_{[j](k)} = \sum\limits_{i = 1}^{{N_{[j](k)} }} {{\mathbf{g}}_{{\{ i\} [j](k)}} \cdot \left( {{\updelta }{\mathbf{u}}_{{\{ i\} }} - {\updelta }{\mathbf{u}}_{(k)} } \right)V_{{\{ i\} }} } . \hfill \\ \end{gathered}$$

(A.2)

The discrete form of ${\updelta }\left( {\nabla \cdot {\mathbf{u}}} \right)_{{{\varvec{\upxi}}}}$ can be recast through (A.2) as

$${\updelta }\left( {\nabla \cdot {\mathbf{u}}} \right)_{[j](k)} = \sum\limits_{i = 1}^{{N_{[j](k)} }} {{\mathbf{B}}_{{\{ i\} [j](k)}}^{{{\text{div}}}} \left( {{\updelta }{\mathbf{u}}_{{\{ i\} }} - {\updelta }{\mathbf{u}}_{(k)} } \right)V_{{\{ i\} }} } = {\mathbf{B}}_{[j](k)}^{{{\text{div}}}} {\updelta }{\mathbf{u}}_{[j](k)} ,$$

(A.3)

where ${\mathbf{B}}_{{\{ i\} [j](k)}}^{{{\text{div}}}} = {\mathbf{g}}_{{\{ i\} [j](k)}}^{{\text{T}}}$. The construction of ${\mathbf{B}}_{[j](k)}^{{{\text{div}}}}$ is the same as Eq. (20).

The bond-associated nonlocal curl of a vector function u and its discrete form can through Eq. (6) be expressed as

$$\begin{gathered} \left( {\nabla \times {\mathbf{u}}} \right)_{{{\varvec{\upxi}}}} = \int_{{H_{{{\varvec{\upxi}}}} }} {{\mathbf{g}}_{{{\varvec{\upxi}}}} ({\overline{\mathbf{\xi }}}) \times \left( {{\mathbf{u}}_{{{\mathbf{x^{\prime\prime}}}}} - {\mathbf{u}}_{{\mathbf{x}}} } \right)dV_{{{\mathbf{x^{\prime\prime}}}}} } \hfill \\ \left( {\nabla \times {\mathbf{u}}} \right)_{[j](k)} = \sum\limits_{i = 1}^{{N_{[j](k)} }} {{\mathbf{g}}_{{\{ i\} [j](k)}} \times \left( {{\mathbf{u}}_{{\{ i\} }} - {\mathbf{u}}_{(k)} } \right)V_{{\{ i\} }} } . \hfill \\ \end{gathered}$$

(A.4)

The variation of $\left( {\nabla \times {\mathbf{u}}} \right)_{{{\varvec{\upxi}}}}$ and its discrete form can be obtained from Eq. (A.4) as

$$\begin{gathered} {\updelta }\left( {\nabla \times {\mathbf{u}}} \right)_{{{\varvec{\upxi}}}} = \int_{{H_{{{\varvec{\upxi}}}} }} {{\mathbf{g}}_{{{\varvec{\upxi}}}} ({\overline{\mathbf{\xi }}}) \times \left( {{\updelta }{\mathbf{u}}_{{{\mathbf{x^{\prime\prime}}}}} - {\updelta }{\mathbf{u}}_{{\mathbf{x}}} } \right)dV_{{{\mathbf{x^{\prime\prime}}}}} } \hfill \\ {\updelta }\left( {\nabla \times {\mathbf{u}}} \right)_{[j](k)} = \sum\limits_{i = 1}^{{N_{[j](k)} }} {{\mathbf{g}}_{{\{ i\} [j](k)}} \times \left( {{\updelta }{\mathbf{u}}_{{\{ i\} }} - {\updelta }{\mathbf{u}}_{(k)} } \right)V_{{\{ i\} }} } . \hfill \\ \end{gathered}$$

(A.5)

The discrete form of ${\updelta }\left( {\nabla \times {\mathbf{u}}} \right)_{{{\varvec{\upxi}}}}$ can be recast through Eq. (A.5) as

$${\updelta }\left( {\nabla \times {\mathbf{u}}} \right)_{[j](k)} = \sum\limits_{i = 1}^{{N_{[j](k)} }} {{\mathbf{B}}_{{\{ i\} [j](k)}}^{{{\text{curl}}}} \left( {{\updelta }{\mathbf{u}}_{{\{ i\} }} - {\updelta }{\mathbf{u}}_{(k)} } \right)V_{{\{ i\} }} } = {\mathbf{B}}_{[j](k)}^{{{\text{curl}}}} {\updelta }{\mathbf{u}}_{[j](k)} ,$$

(A.6)

where the construction of ${\mathbf{B}}_{[j](k)}^{{{\text{curl}}}}$ is the same as Eq. (20) and ${\mathbf{B}}_{{\{ i\} [j](k)}}^{{{\text{curl}}}}$ is given by

$${\mathbf{B}}_{{\{ i\} [j](k)}}^{{{\text{curl}}}} = \left[ {\begin{array}{*{20}c} 0 & { - g_{{\{ i\} [j](k)}}^{001} } & {g_{{\{ i\} [j](k)}}^{010} } \\ {g_{{\{ i\} [j](k)}}^{001} } & 0 & { - g_{{\{ i\} [j](k)}}^{100} } \\ { - g_{{\{ i\} [j](k)}}^{010} } & {g_{{\{ i\} [j](k)}}^{100} } & 0 \\ \end{array} } \right].$$

(A.7)

The bond-associated nonlocal gradient of divergence for a vector function u and its discrete form can be expressed through Eq. (6) as

$$\begin{gathered} \left( {\nabla \otimes \nabla \cdot {\mathbf{u}}} \right)_{{{\varvec{\upxi}}}} = \int_{{H_{{{\varvec{\upxi}}}} }} {{\hat{\mathbf{g}}}_{{{\varvec{\upxi}}}} ({\overline{\mathbf{\xi }}}) \cdot \left( {{\mathbf{u}}_{{{\mathbf{x^{\prime\prime}}}}} - {\mathbf{u}}_{{\mathbf{x}}} } \right)dV_{{{\mathbf{x^{\prime\prime}}}}} } \hfill \\ \left( {\nabla \otimes \nabla \cdot {\mathbf{u}}} \right)_{[j](k)} = \sum\limits_{i = 1}^{{N_{[j](k)} }} {{\hat{\mathbf{g}}}_{{\{ i\} [j](k)}} \otimes \left( {{\mathbf{u}}_{{\{ i\} }} - {\mathbf{u}}_{(k)} } \right)V_{{\{ i\} }} } , \hfill \\ \end{gathered}$$

(A.8)

where

$${\hat{\mathbf{g}}}_{{{\varvec{\upxi}}}} ({\overline{\mathbf{\xi }}}) = \left[ {\begin{array}{*{20}c} {g_{{{{\varvec{\upxi}}}N}}^{200} ({\overline{\mathbf{\xi }}})} & {g_{{{{\varvec{\upxi}}}N}}^{110} ({\overline{\mathbf{\xi }}})} & {g_{{{{\varvec{\upxi}}}N}}^{101} ({\overline{\mathbf{\xi }}})} \\ {g_{{{{\varvec{\upxi}}}N}}^{110} ({\overline{\mathbf{\xi }}})} & {g_{{{{\varvec{\upxi}}}N}}^{020} ({\overline{\mathbf{\xi }}})} & {g_{{{{\varvec{\upxi}}}N}}^{011} ({\overline{\mathbf{\xi }}})} \\ {g_{{{{\varvec{\upxi}}}N}}^{101} ({\overline{\mathbf{\xi }}})} & {g_{{{{\varvec{\upxi}}}N}}^{011} ({\overline{\mathbf{\xi }}})} & {g_{{{{\varvec{\upxi}}}N}}^{002} ({\overline{\mathbf{\xi }}})} \\ \end{array} } \right],\;{\hat{\mathbf{g}}}_{{\{ i\} [j](k)}} = \left[ {\begin{array}{*{20}c} {g_{{\{ i\} [j](k)}}^{200} } & {g_{{\{ i\} [j](k)}}^{110} } & {g_{{\{ i\} [j](k)}}^{101} } \\ {g_{{\{ i\} [j](k)}}^{110} } & {g_{{\{ i\} [j](k)}}^{020} } & {g_{{\{ i\} [j](k)}}^{011} } \\ {g_{{\{ i\} [j](k)}}^{101} } & {g_{{\{ i\} [j](k)}}^{011} } & {g_{{\{ i\} [j](k)}}^{002} } \\ \end{array} } \right].$$

(A.9)

The variation of $\left( {\nabla \otimes \nabla \cdot {\mathbf{u}}} \right)_{{{\varvec{\upxi}}}}$ and its discrete form can be obtained from Eq. (A.9) as

$$\begin{gathered} {\updelta }\left( {\nabla \otimes \nabla \cdot {\mathbf{u}}} \right)_{{{\varvec{\upxi}}}} = \int_{{H_{{{\varvec{\upxi}}}} }} {{\hat{\mathbf{g}}}_{{{\varvec{\upxi}}}} ({\overline{\mathbf{\xi }}}) \cdot \left( {{\updelta }{\mathbf{u}}_{{{\mathbf{x^{\prime\prime}}}}} - {\updelta }{\mathbf{u}}_{{\mathbf{x}}} } \right)dV_{{{\mathbf{x^{\prime\prime}}}}} } \hfill \\ {\updelta }\left( {\nabla \otimes \nabla \cdot {\mathbf{u}}} \right)_{[j](k)} = \sum\limits_{i = 1}^{{N_{[j](k)} }} {{\hat{\mathbf{g}}}_{{\{ i\} [j](k)}} \cdot \left( {{\updelta }{\mathbf{u}}_{{\{ i\} }} - {\updelta }{\mathbf{u}}_{(k)} } \right)V_{{\{ i\} }} } . \hfill \\ \end{gathered}$$

(A.10)

The discrete form of ${\updelta }\left( {\nabla \otimes \nabla \cdot {\mathbf{u}}} \right)_{{{\varvec{\upxi}}}}$ can be recast through Eq. (A.10) as

$${\updelta }\left( {\nabla \otimes \nabla \cdot {\mathbf{u}}} \right)_{[j](k)} = \sum\limits_{i = 1}^{{N_{[j](k)} }} {{\mathbf{B}}_{{\{ i\} [j](k)}}^{{\text{grad - div}}} \left( {{\updelta }{\mathbf{u}}_{{\{ i\} }} - {\updelta }{\mathbf{u}}_{(k)} } \right)} V_{{\{ i\} }} = {\mathbf{B}}_{[j](k)}^{{\text{grad - div}}} {\updelta }{\mathbf{u}}_{[j](k)} ,$$

(A.11)

where ${\mathbf{B}}_{{\{ i\} [j](k)}}^{{\text{grad - div}}} = {\hat{\mathbf{g}}}_{{\{ i\} [j](k)}}^{{\text{T}}}$. The construction of ${\mathbf{B}}_{[j](k)}^{{\text{grad - div}}}$ is the same as Eq. (20).

The bond-associated nonlocal Laplacian for a vector function u and its discrete form can be expressed through Eq. (6) as

$$\begin{gathered} \left( {\nabla^{2} {\mathbf{u}}} \right)_{{{\varvec{\upxi}}}} = \int_{{H_{{{\varvec{\upxi}}}} }} {{\text{tr}}({\hat{\mathbf{g}}}_{{{\varvec{\upxi}}}} ({\overline{\mathbf{\xi }}}))\left( {{\mathbf{u}}_{{{\mathbf{x^{\prime\prime}}}}} - {\mathbf{u}}_{{\mathbf{x}}} } \right)dV_{{{\mathbf{x^{\prime\prime}}}}} } \hfill \\ \left( {\nabla^{2} {\mathbf{u}}} \right)_{[j](k)} = \sum\limits_{i = 1}^{{N_{[j](k)} }} {{\text{tr}}({\hat{\mathbf{g}}}_{{\{ i\} [j](k)}} )\left( {{\mathbf{u}}_{{\{ i\} }} - {\mathbf{u}}_{(k)} } \right)V_{{\{ i\} }} } . \hfill \\ \end{gathered}$$

(A.12)

The variation of $\left( {\nabla^{2} {\mathbf{u}}} \right)_{{{\varvec{\upxi}}}}$ and its discrete form can be obtained from Eq. (A.12) as

$$\begin{gathered} {\updelta }\left( {\nabla^{2} {\mathbf{u}}} \right)_{{{\varvec{\upxi}}}} = \int_{{H_{{{\varvec{\upxi}}}} }} {{\text{tr}}({\hat{\mathbf{g}}}_{{{\varvec{\upxi}}}} ({\overline{\mathbf{\xi }}}))\left( {{\updelta }{\mathbf{u}}_{{{\mathbf{x^{\prime\prime}}}}} - {\updelta }{\mathbf{u}}_{{\mathbf{x}}} } \right)dV_{{{\mathbf{x^{\prime\prime}}}}} } \hfill \\ {\updelta }\left( {\nabla^{2} {\mathbf{u}}} \right)_{[j](k)} = \sum\limits_{i = 1}^{{N_{[j](k)} }} {{\text{tr}}({\hat{\mathbf{g}}}_{{\{ i\} [j](k)}} )\left( {{\updelta }{\mathbf{u}}_{{\{ i\} }} - {\updelta }{\mathbf{u}}_{(k)} } \right)V_{{\{ i\} }} } . \hfill \\ \end{gathered}$$

(A.13)

The discrete form of ${\updelta }\left( {\nabla^{2} {\mathbf{u}}} \right)_{{{\varvec{\upxi}}}}$ can be recast through Eq. (A.13) as

$${\updelta }\left( {\nabla^{2} {\mathbf{u}}} \right)_{[j](k)} = \sum\limits_{i = 1}^{{N_{[j](k)} }} {{\mathbf{B}}_{{\{ i\} [j](k)}}^{{{\text{Lapl}}}} \left( {{\updelta }{\mathbf{u}}_{{\{ i\} }} - {\updelta }{\mathbf{u}}_{(k)} } \right)} V_{{\{ i\} }} = {\mathbf{B}}_{[j](k)}^{{{\text{Lapl}}}} {\updelta }{\mathbf{u}}_{[j](k)} ,$$

(A.14)

where ${\mathbf{B}}_{{\{ i\} [j](k)}}^{{{\text{Lapl}}}} = {\text{tr}}({\hat{\mathbf{g}}}_{{\{ i\} [j](k)}} ){\mathbf{I}}$. The construction of ${\mathbf{B}}_{[j](k)}^{{{\text{Lapl}}}}$ is the same as Eq. (20).