Skip to main content

Advertisement

Springer Nature Link
Log in

A deep learning-based multi-fidelity optimization method for the design of acoustic metasurface

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

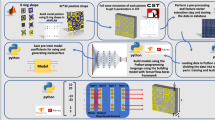
Abstract

A desirable acoustic metasurface requires the scattered acoustic field distribution uniform. Neural networks are effective substitutions to mimic the expensive FE simulations in most research. However, the computational cost required to construct a model with only single high-fidelity (HF) simulation data is still unacceptable. This paper presents a deep learning-based multi-fidelity optimization framework to improve the uniformity of the scattered acoustic field distribution. First, a multi-fidelity composite convolutional neural network (MF-CCNN) method is proposed to predict the high-dimensional scattered acoustic field at a lower data cost. The developed MF-CCNN consists of four convolutional subnets. The first part predicts a low-fidelity (LF) output, whose features are then extracted by the second part and concatenated with the inputs to predict the HF result. Two parallel branches are utilized to map the LF features to the HF output. Then, the physical parameters’ optimization neural network is proposed to minimize the objective under the prediction of MF-CCNN. The proposed method is compared with other state-of-the-art multi-fidelity networks, and the results demonstrate that MF-CCNN reaches the highest accuracy and the mean absolute error is improved by at least 20%. The variance of the obtained scattered acoustic field after optimization is reduced by 3.62%, and the time cost is only 8% of the genetic algorithm (GA), proving the efficiency and accuracy of the proposed framework.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23

Similar content being viewed by others

Data availability statement

The data that support the findings of this study are available from the corresponding author on reasonable request.

References

  1. Ma G, Sheng P (2016) Acoustic metamaterials: From local resonances to broad horizons. Sci Adv 2:e1501595

    Article  Google Scholar 

  2. Cummer SA, Christensen J, Alù A (2016) Controlling sound with acoustic metamaterials. Nat Rev Mater 1:1–13

    Article  Google Scholar 

  3. Xie Y, Wang W, Chen H, Konneker A, Popa B-I, Cummer SA (2014) Wavefront modulation and subwavelength diffractive acoustics with an acoustic metasurface. Nat Commun 5:1–5

    Article  Google Scholar 

  4. Zhu Y, Fan X, Liang B, Cheng J, Jing Y (2017) Ultrathin acoustic metasurface-based Schroeder diffuser. Phys Rev X 7:021034

    Google Scholar 

  5. Liao G, Wang Z, Luan C, Liu J, Yao X, Fu J (2021) Broadband controllable acoustic focusing and asymmetric focusing by acoustic metamaterials. Smart Mater Struct 30:045021

    Article  Google Scholar 

  6. Almeida GDN, Vergara EF, Barbosa LR, Lenzi A, Birch RS (2021) Sound absorption metasurface with symmetrical coiled spaces and micro slit of variable depth. Appl Acoust 183:108312

    Article  Google Scholar 

  7. Popa B-I, Zigoneanu L, Cummer SA (2011) Experimental acoustic ground cloak in air. Phys Rev Lett 106:253901

    Article  Google Scholar 

  8. Jiang X, Liang B, Cheng JC, Qiu CW (2018) Twisted acoustics: metasurface-enabled multiplexing and demultiplexing. Adv Mater 30:1800257

    Article  Google Scholar 

  9. Assouar B, Liang B, Wu Y, Li Y, Cheng J-C, Jing Y (2018) Acoustic metasurfaces. Nat Rev Mater 3:460–472

    Article  Google Scholar 

  10. Ma G, Yang M, Xiao S, Yang Z, Sheng P (2014) Acoustic metasurface with hybrid resonances. Nat Mater 13:873–878

    Article  Google Scholar 

  11. Cao L, Yang Z, Xu Y, Fan S-W, Zhu Y, Chen Z, Li Y, Assouar B (2020) Flexural wave absorption by lossy gradient elastic metasurface. J Mech Phys Solids 143:104052

    Article  MathSciNet  Google Scholar 

  12. Yu N, Genevet P, Kats MA, Aieta F, Tetienne J-P, Capasso F, Gaburro Z (2011) Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334:333–337

    Article  Google Scholar 

  13. Zhao Y, Liu J, Liang B, Cheng J (2020) An ultrathin planar acoustic metasurface diffuser with narrowband uniform reflection. AIP Adv 10:085122

    Article  Google Scholar 

  14. Ma G, Fan X, Sheng P, Fink M (2018) Shaping reverberating sound fields with an actively tunable metasurface. Proc Natl Acad Sci 115:6638–6643

    Article  Google Scholar 

  15. Gao H, Zhu Y-F, Fan X-D, Liang B, Yang J, Cheng J-C (2017) Non-blind acoustic invisibility by dual layers of homogeneous single-negative media. Sci Rep 7:1–7

    Google Scholar 

  16. Miyata K, Noguchi Y, Yamada T, Izui K, Nishiwaki S (2018) Optimum design of a multi-functional acoustic metasurface using topology optimization based on Zwicker’s loudness model. Comput Methods Appl Mech Eng 331:116–137

    Article  MathSciNet  MATH  Google Scholar 

  17. Bhosekar A, Ierapetritou M (2018) Advances in surrogate based modeling, feasibility analysis, and optimization: a review. Comput Chem Eng 108:250–267

    Article  Google Scholar 

  18. Jin X, Cheng P, Chen W-L, Li H (2018) Prediction model of velocity field around circular cylinder over various Reynolds numbers by fusion convolutional neural networks based on pressure on the cylinder. Phys Fluids 30:047105

    Article  Google Scholar 

  19. Bhatnagar S, Afshar Y, Pan S, Duraisamy K, Kaushik S (2019) Prediction of aerodynamic flow fields using convolutional neural networks. Comput Mech 64:525–545

    Article  MathSciNet  MATH  Google Scholar 

  20. Rüttgers M, Koh S-R, Jitsev J, Schröder W, Lintermann A (2020) Prediction of acoustic fields using a lattice-Boltzmann method and deep learning. International Conference on High Performance Computing, Springer, pp 81–101

  21. Tian J, Qi C, Sun Y, Yaseen ZM, Pham BT (2021) Permeability prediction of porous media using a combination of computational fluid dynamics and hybrid machine learning methods. Eng Comput 37:3455–3471

    Article  Google Scholar 

  22. Liang L, Liu M, Martin C, Sun W (2018) A deep learning approach to estimate stress distribution: a fast and accurate surrogate of finite-element analysis. J R Soc Interface 15:20170844

    Article  Google Scholar 

  23. Nie Z, Jiang H, Kara LB (2020) Stress field prediction in cantilevered structures using convolutional neural networks. J Comput Inf Sci Eng 20:011002

    Article  Google Scholar 

  24. Guo X, Li W, Iorio F (2016), Convolutional neural networks for steady flow approximation. In: Proceedings of the 22nd ACM SIGKDD International Conference on knowledge discovery and data mining, pp 481–490.

  25. Sekar V, Jiang Q, Shu C, Khoo BC (2019) Fast flow field prediction over airfoils using deep learning approach. Phys Fluids 31:057103

    Article  Google Scholar 

  26. Kim B, Azevedo VC, Thuerey N, Kim T, Gross M, Solenthaler B (2019) Deep fluids: a generative network for parameterized fluid simulations. Comput Graph Forum 38:59–70

  27. Wu H, Liu X, An W, Chen S, Lyu H (2020) A deep learning approach for efficiently and accurately evaluating the flow field of supercritical airfoils. Comput Fluids 198:104393

    Article  MathSciNet  MATH  Google Scholar 

  28. Fan Z, Vineet V, Gamper H, Raghuvanshi N (2020), Fast acoustic scattering using convolutional neural networks. In: ICASSP 2020–2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), IEEE, 2020, pp 171–175

  29. Donda K, Zhu Y, Merkel A, Fan S-W, Cao L, Wan S, Assouar B (2021) Ultrathin acoustic absorbing metasurface based on deep learning approach. Smart Mater Struct 30:085003

    Article  Google Scholar 

  30. Zhao T, Li Y, Zuo L, Zhang K (2021) Machine-learning optimized method for regional control of sound fields. Extreme Mech Lett 45:101297

    Article  Google Scholar 

  31. Nansha G, Mou W, Baozhu C (2022) Deep auto-encoder network in predictive design of Helmholtz resonator: on-demand prediction of sound absorption peak. Appl Acoust 191:108680

    Article  Google Scholar 

  32. Liao Z, Wang Y, Gao L, Wang Z-P (2022) Deep-learning-based isogeometric inverse design for tetra-chiral auxetics. Compos Struct 280:114808

    Article  Google Scholar 

  33. Zhou K, Tang J (2021) Efficient characterization of dynamic response variation using multi-fidelity data fusion through composite neural network. Eng Struct 232:111878

    Article  Google Scholar 

  34. De S, Britton J, Reynolds M, Skinner R, Jansen K, Doostan A (2020) On transfer learning of neural networks using bi-fidelity data for uncertainty propagation. Int J Uncertain Quant 10:543–573

    Article  MathSciNet  MATH  Google Scholar 

  35. Liu J, Yi J, Zhou Q, Cheng Y (2022) A sequential multi-fidelity surrogate model-assisted contour prediction method for engineering problems with expensive simulations. Eng Comput 38:31–49

    Article  Google Scholar 

  36. Liu D, Wang Y (2019) Multi-fidelity physics-constrained neural network and its application in materials modeling. J Mech Des 141:121403

  37. Meng X, Karniadakis GE (2020) A composite neural network that learns from multi-fidelity data: Application to function approximation and inverse PDE problems. J Comput Phys 401:109020

    Article  MathSciNet  MATH  Google Scholar 

  38. Zhang X, Xie F, Ji T, Zhu Z, Zheng Y (2021) Multi-fidelity deep neural network surrogate model for aerodynamic shape optimization. Comput Methods Appl Mech Eng 373:113485

    Article  MathSciNet  MATH  Google Scholar 

  39. Aieta F, Kabiri A, Genevet P, Yu N, Kats MA, Gaburro Z, Capasso F (2012) Reflection and refraction of light from metasurfaces with phase discontinuities. J Nanophotonics 6:063532

    Article  Google Scholar 

  40. Kennedy MC, O’Hagan A (2000) Predicting the output from a complex computer code when fast approximations are available. Biometrika 87:1–13

    Article  MathSciNet  MATH  Google Scholar 

  41. Karniadakis GE, Kevrekidis IG, Lu L, Perdikaris P, Wang S, Yang L (2021) Physics-informed machine learning. Nat Rev Phys 3:422–440

    Article  Google Scholar 

  42. Raissi M, Perdikaris P, Karniadakis GE (2019) Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys 378:686–707

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This research has been partially supported by the National Natural Science Foundation of China (NSFC) under Grant Nos. 52175231, 52105254, 52105256, and the Research Funds of the Maritime Defense Technologies Innovation Nos. JJ2021-719-02, JJ2021-719-03, and JJ2020-719-03-01.

Author information

Authors and Affiliations

  1. School of Aerospace Engineering, Huazhong University of Science and Technology, Wuhan, 430074, Hubei, China

    Jinhong Wu, Xufeng Huang & Qi Zhou

  2. Wuhan Second Ship Design and Research Institute, Wuhan, 430064, Hubei, China

    Xingxing Feng & Xuan Cai

Authors
  1. Jinhong Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xingxing Feng
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Xuan Cai
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Xufeng Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Qi Zhou
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Qi Zhou.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, J., Feng, X., Cai, X. et al. A deep learning-based multi-fidelity optimization method for the design of acoustic metasurface. Engineering with Computers 39, 3421–3439 (2023). https://doi.org/10.1007/s00366-022-01765-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-022-01765-9

Keywords