Bond-based peridynamic modeling of fiber-reinforced composite laminates with stretch and rotation kinematics

Abstract

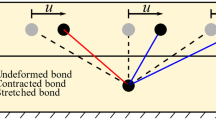
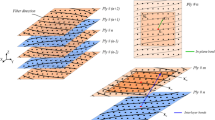
This study presents the bond-based (BB) peridynamics (PD) with stretch and rotation kinematics for modeling the linear elastic deformation of a composite laminate. The laminate experiences only in-plane and transverse shear deformations and disregards the transverse normal deformation. The PD equilibrium equation for a laminate is derived under the assumption of small deformation and is solved by employing implicit techniques. The in-plane PD forces are expressed by considering the PD bond interactions among the points. The forces arising from the interaction of adjacent layers are expressed by considering a pointwise approach that utilizes the PD differential operator (PDDO) in conjunction with the shear-lag theory. The micro-moduli associated with stretch and rotation are directly related to the constitutive relations between stress and strain components in continuum mechanics. It is restricted to only one constraint on the material constants leading to a fixed value of in-plane shear modulus. The accuracy of this approach is demonstrated by capturing the correct deformation in a laminate for varying layups. Finally, its capability for progressive failure is demonstrated by considering a quasi-isotropic laminate with a pre-existing crack. It employs critical stretch, the critical skew (relative rotation) angle and the critical delamination angle in the bond breakage criteria.

Appendices

Appendix A

The correction factor can be determined by calibrating the PD SED associated with fiber deformation against that of CCM by considering a simple strain state of $\varepsilon_{11} \ne 0,\,\,\varepsilon_{22} = \gamma_{12} = 0$. For this strain state, the classical SED at point, $x_{1(k)}$ along the fiber can be evaluated as

$$W_{f(k)} = \frac{1}{2}\left( {Q_{11} - Q_{22} } \right)\varepsilon_{11}^{2} ,$$

(88)

The PD SED can be evaluated from Eq. (6) as

$$W_{f(k)}^{PD} = \frac{1}{4}\sum\limits_{j = 1}^{{N_{(k)}^{f} }} {c_{f} s_{(k)(j)}^{2} \xi_{(k)(j)} V_{(j)} } ,$$

(89)

or

$$W_{f(k)}^{PD} = \frac{1}{4}\sum\limits_{j = 1}^{{N_{(k)}^{f} }} {c_{f} } \left( {\frac{{u_{1(j)} - u_{1(k)} }}{{\xi_{(k)(j)} }}} \right)^{2} \xi_{(k)(j)} V_{(j)} ,$$

(90)

where $u_{1(j)}$ and $u_{1(k)}$ denote, respectively, the displacement components at points $x_{1(j)}$ and $x_{1(k)}$ in the fiber direction only, and $N_{(k)}^{f}$ is the number of family members of point, $x_{1(k)}$ associated with the fiber bonds. The displacement components corresponding to the applied strain state can be expressed as

$$u_{1(k)} = \varepsilon_{11} x_{1(k)} ,$$

(91a)

and

$$u_{1(j)} = \varepsilon_{11} x_{1(j)} ,$$

(91b)

with $x_{1(k)}$ and $x_{1(j)}$ denoting the coordinates in the fiber direction with respect to the material coordinate systems, $(x_{1} ,y_{1} )$.

The surface correction for the fiber bonds at point $x_{1(k)}$ is defined as

$$S_{(k)}^{f} = \frac{{W_{f(k)} }}{{W_{f(k)}^{PD} }} = \frac{{2\left( {Q_{11} - Q_{22} } \right)}}{{\sum\limits_{j = 1}^{{N_{(k)}^{f} }} {c_{f} } \left( {x_{1(j)} - x_{1(k)} } \right)V_{(j)} }},$$

(92)

Substituting for $c_{f}$ from Eq. (39) in this equation results in

$$S_{(k)}^{f} = \frac{{W_{f(k)} }}{{W_{f(k)}^{PD} }} = \frac{{hI_{f} }}{{\sum\limits_{j = 1}^{{N_{(k)}^{f} }} {(x_{1(j)} - x_{1(k)} )V_{(j)} } }},$$

(93)

Hence, the surface correction factor, $S_{(k)(j)}^{f}$ for a bond between $x_{1(k)}$ to $x_{1(j)}$ can be approximated as

$$S_{(k)(j)}^{f} = \frac{1}{2}\left( {S_{(k)}^{f} + S_{(j)}^{f} } \right).$$

(94)

Appendix B

The matrices ${\mathbf{H}}_{(k)(j)}^{(k)}$ of order $(3 \times 3K)$ and ${\mathbf{H}}_{(k)(j)}^{(j)}$ of order $(3 \times 3J)$ appearing in Eq. (60) are defined in the form

$${\mathbf{H}}_{(k)(j)}^{(k)} = \left[ {\begin{array}{*{20}c} { - \sum\limits_{\ell = 1}^{K} {{\mathbf{G}}_{(k)(j)}^{{(k_{\ell } )}} } } & {{\mathbf{G}}_{(k)(j)}^{{(k_{1} )}} } & {{\mathbf{G}}_{(k)(j)}^{{(k_{2} )}} } & \cdots & {{\mathbf{G}}_{(k)(j)}^{{(k_{K} )}} } \\ \end{array} } \right],$$

(95a)

and

$${\mathbf{H}}_{(k)(j)}^{(j)} = \left[ {\begin{array}{*{20}c} { - \sum\limits_{\ell = 1}^{J} {{\mathbf{G}}_{(k)(j)}^{{(j_{\ell } )}} } } & {{\mathbf{G}}_{(k)(j)}^{{(j_{1} )}} } & {{\mathbf{G}}_{(k)(j)}^{{(j_{2} )}} } & \cdots & {{\mathbf{G}}_{(k)(j)}^{{(j_{J} )}} } \\ \end{array} } \right],$$

(95b)

where the matrix of PD function ${\mathbf{G}}_{(k)(j)}^{{(\alpha_{\ell } )}}$ with $(\alpha = k,j)$ is defined as

$${\mathbf{G}}_{(k)(j)}^{{(\alpha_{\ell } )}} = \frac{1}{2}\left[ {\begin{array}{*{20}c} {\xi_{2(k)(j)} g_{{2(\alpha_{\ell } )}}^{010} + \xi_{3(k)(j)} g_{{2(\alpha_{\ell } )}}^{001} } & { - \xi_{2(k)(j)} g_{{2(\alpha_{\ell } )}}^{100} } & { - \xi_{3(k)(j)} g_{{2(\alpha_{\ell } )}}^{100} } \\ { - \xi_{1(k)(j)} g_{{2(\alpha_{\ell } )}}^{010} } & {\xi_{1(k)(j)} g_{{2(\alpha_{\ell } )}}^{100} + \xi_{3(k)(j)} g_{{2(\alpha_{\ell } )}}^{001} } & { - \xi_{3(k)(j)} g_{{2(\alpha_{\ell } )}}^{010} } \\ { - \xi_{1(k)(j)} g_{{2(\alpha_{\ell } )}}^{001} } & { - \xi_{2(k)(j)} g_{{2(\alpha_{\ell } )}}^{001} } & {\xi_{1(k)(j)} g_{{2(\alpha_{\ell } )}}^{100} + \xi_{2(k)(j)} g_{{2(\alpha_{\ell } )}}^{010} } \\ \end{array} } \right].$$

(96)

Appendix C

The relative displacements between layers $\ell$ and $u$ due to effective transverse shear strain vector, ${{\varvec{\upgamma}}}^{(\ell ,u)}$, can be expressed in terms of the transverse shear deformation vectors of layers $\ell$ and $u$ as

$${{\varvec{\upgamma}}}^{(\ell ,u)} t^{(\ell ,u)} = {{\varvec{\upgamma}}}^{(\ell )} \frac{{t^{(\ell )} }}{2} + {{\varvec{\upgamma}}}^{(u)} \frac{{t^{(u)} }}{2},$$

(97)

where ${{\varvec{\upgamma}}}^{(\ell )}$ and denote the transverse shear strain vectors of layers $\ell$ and $u$, respectively. From the strain–stress relationship, Eq. (97) can be rewritten as

$$2t^{(\ell ,u)} {\mathbf{S}}^{(\ell ,u)} {{\varvec{\uptau}}}^{(\ell ,u)} = t^{(\ell )} {\mathbf{S}}^{(\ell )} {{\varvec{\uptau}}}^{(\ell )} + t^{(u)} {\mathbf{S}}^{(u)} {{\varvec{\uptau}}}^{(u)} ,$$

(98)

where ${\mathbf{S}}^{(\ell )}$ and ${\mathbf{S}}^{(\ell )}$ represent the compliance matrices relating transverse shear stress vectors to tra ${{\varvec{\upgamma}}}^{(u)}$ nsverse shear strain vectors in layers $\ell$ and $u$, respectively. Similarly, ${\mathbf{S}}^{(\ell )}$ denotes the effective compliance matrix relating the effective transverse stress vector to the effective transverse strain vector. It is assumed that ${{\varvec{\uptau}}}^{(\ell ,u)} = {{\varvec{\uptau}}}^{(\ell )} = {{\varvec{\uptau}}}^{(u)}$ throughout the interface between $\ell$ and $u$. Hence, replacing ${{\varvec{\uptau}}}^{(\ell )}$ and ${{\varvec{\uptau}}}^{(u)}$ with ${{\varvec{\uptau}}}^{(\ell ,u)}$, Eq. (98) becomes

$$2t^{(\ell ,u)} {\mathbf{S}}^{(\ell ,u)} {{\varvec{\uptau}}}^{(\ell ,u)} = t^{(\ell )} {\mathbf{S}}^{(\ell )} {{\varvec{\uptau}}}^{(\ell ,u)} + t^{(u)} {\mathbf{S}}^{(u)} {{\varvec{\uptau}}}^{(\ell ,u)} ,$$

(99)

or after rearranging

$$\left( {2t^{(\ell ,u)} {\mathbf{S}}^{(\ell ,u)} - t^{(\ell )} {\mathbf{S}}^{(\ell )} - t^{(u)} {\mathbf{S}}^{(u)} } \right){{\varvec{\uptau}}}^{(\ell ,u)} = {\mathbf{0}},$$

(100)

Equation (100) leads to the expression for an effective compliance matrix in terms of the compliance matrices of layers $\ell$ and $u$ as

$${\mathbf{S}}^{(\ell ,u)} = \frac{{t^{(\ell )} {\mathbf{S}}^{(\ell )} + t^{(u)} {\mathbf{S}}^{(u)} }}{{2t^{(\ell ,u)} }},$$

(101)

Note that ${\mathbf{S}}^{(\ell )} = {\mathbf{C}}^{{(\ell )^{ - 1} }}$ and ${\mathbf{S}}^{(u)} = {\mathbf{C}}^{{(u)^{ - 1} }}$. Hence, in terms of stiffness matrices of layers $\ell$ and $u$, The effective compliance matrix, ${\mathbf{S}}^{(\ell ,u)}$, is expressed as

$${\mathbf{S}}^{(\ell ,u)} = \frac{{t^{(\ell )} {\mathbf{C}}^{{(\ell )^{ - 1} }} + t^{(u)} {\mathbf{C}}^{{(u)^{ - 1} }} }}{{2t^{(\ell ,u)} }},$$

(102)

Inverting Eq. (102) yields $\ell$ the effective stiffness matrix of the interface between layers and $u$, ${\mathbf{C}}^{(\ell ,u)}$, being expressed in terms of the stiffness matrices of the layers and $u$ as

$$\ell$$

$${\mathbf{C}}^{(\ell ,u)} = {\mathbf{S}}^{{(\ell ,u)^{ - 1} }} = \left( {\frac{{t^{(\ell )} {\mathbf{C}}^{{(\ell )^{ - 1} }} + t^{(u)} {\mathbf{C}}^{{(u)^{ - 1} }} }}{{2t^{(\ell ,u)} }}} \right)^{ - 1} = \left( {\frac{{t^{(\ell )} {\mathbf{C}}^{{(\ell )^{ - 1} }} + t^{(u)} {\mathbf{C}}^{{(u)^{ - 1} }} }}{{t^{(\ell )} + t^{(u)} }}} \right)^{ - 1} ,$$

(103)

where $t^{(\ell ,u)} = \frac{1}{2}\left( {t^{(\ell )} + t^{(u)} } \right)$. Finally, the resultant interlayer shear stiffness coefficients are computed by

$${\mathbf{G}}_{\gamma }^{(\ell ,u)} = t^{(\ell ,u)} {\mathbf{C}}^{(\ell ,u)} = \left( {\frac{{t^{(\ell )} {\mathbf{C}}^{{(\ell )^{ - 1} }} + t^{(u)} {\mathbf{C}}^{{(u)^{ - 1} }} }}{{2\left( {t^{(\ell ,u)} } \right)^{2} }}} \right)^{ - 1} .$$

(104)