Meshing using neural networks for improving the efficiency of computer modelling

Abstract

This work presents a novel approach capable of predicting an appropriate spacing function that can be used to generate a near-optimal mesh suitable for simulation. The main objective is to make use of the large number of simulations that are nowadays available, and to alleviate the time-consuming mesh generation stage by minimising human intervention. For a given simulation, a technique to produce a set of point sources that leads to a mesh capable of capturing all the features of the solution is proposed. In addition, a method to combine all sets of sources for the simulations available is devised. The global set of sources is used to train a neural network that, for some design parameters (e.g., flow conditions, geometry), predicts the characteristics of the sources. Numerical examples, in the context of three dimensional inviscid compressible flows, are considered to demonstrate the potential of the proposed approach. It is shown that accurate predictions of the required spacing function can be produced, even with reduced training datasets. In addition, the predicted near-optimal meshes are utilised to compute flow solutions, and the results show that the computed aerodynamic coefficients are within the required accuracy for the aerospace industry. An analysis is also presented to demonstrate that the proposed method lies in the category of green AI research, meaning that computational resources and time are substantially reduced with this approach, when compared to current practice in industry.

1 Introduction

Computational methods are increasingly used to complement experiments and analysis in many areas of science and engineering. The large majority of numerical methods used to simulate physical phenomena require the generation of a mesh that describes the geometry under consideration. The process of generating unstructured meshes of complex geometries is still recognised as one of the bottlenecks of the computational fluid dynamics (CFD) simulation pipeline [1,2,3].

All mesh generation strategies require the specification of a spacing function that controls the size of the generated elements in the domain. The spacing function utilised must lead to a mesh that is only refined in the vicinity of regions that contain complex features that need to be resolved. Different approaches are usually considered to define the spacing function, namely the use of a background structured or unstructured mesh [4], refinement based on boundary curvature [5], the specification of the spacing at certain geometric entities and the use of point, line or triangular sources [5, 6]. Sources are usually preferred for complex geometric models in three dimensions due to the greater flexibility they offer. In addition, using sources can complement the use of background meshes, the refinement based on boundary curvature and/or the refinement based on geometric entities. However, defining an appropriate set of sources for complex models is still time consuming and it requires a significant level of human intervention.

In recent years, mesh adaptive processes have gained popularity [7]. With these approaches, the user only needs to define an initial coarse mesh. An iterative and automatic process ensures that the mesh is successively refined, only where needed, to accurately capture the solution. Despite the potential of such approaches, it is known that an inadequate initial mesh may result in some unresolved features, even after many refinement loops. In addition, mesh adaptive algorithms have shown that a significant number of refinement loops, between 20 and 30, might be required to reach the required accuracy [8]. It is worth noting that each loop requires a computation, estimating the error of the computed solution, generating an adapted mesh and the interpolation of the solution from the old to the new mesh.

The objective of this work is to develop a technique, based on neural networks (NNs), that enables the prediction of a near-optimal mesh suitable for simulation. The main idea is to make use of the vast volume of data, that already exists in industry, to optimise the selection of a suitable spacing function. The proposed approach aims at exploiting the knowledge embedded in previous simulations to inform the mesh generation stage. In addition, it has the potential to alleviate the recurrent problem of mesh generation being a major bottleneck in the CFD simulation pipeline. The technique presented can also be used to predict a mesh to be used in an adaptive process. In this scenario, it is anticipated that the number of refinement loops required would significantly decrease, when compared to a naive choice of the initial mesh.

The proposed strategy consists of four stages. First, a technique to produce a set of point sources from an existing solution is proposed. The use of point sources, contrary to other type of sources, is considered here to reduce the parameters associated with each source and to enable the possibility to group sources in a latter stage. For each available solution, a set of point sources that leads to a mesh capable of capturing all the solution features is created. The process is based on well established concepts of error estimation and a recovery process to compute the Hessian matrix of a key variable at the nodes of the given mesh. With this information, a novel process is presented to create point sources that lead to a continuous spacing function that closely represent the discrete spacing function induced by the calculated spacing at the nodes. This step is repeated for all the solutions available, leading to different sets of point sources. To ensure that the data can be used to train a NN, an approach to combine the sources of each case into a global set of sources is proposed. The strategy ensures that the final set of sources can represent the spacing function for all the cases available. By using the global set of sources, a NN is devised. The inputs are the design parameters (e.g. flow conditions, geometric parameters) and the outputs are the characteristics of all the mesh sources (i.e., position of the sources, spacing and radius of influence). After the NN is trained, it can be used to predict the spacing function required for unseen cases and, ultimately, to predict a near-optimal mesh for a new simulation. To speed up the generation of the near-optimal meshes, a novel approach to merge point sources into line sources is also proposed. The approach is based on the total least-squares [9] and it ensures that, during the mesh generation stage, the number of queries required to calculate the spacing at a point is reduced.

The starting point considered here is a set of accurate solutions that are available in an industrial environment. It is worth noting that the solutions might have been computed in over-refined meshes with the objective to minimise the human intervention required to create an optimal mesh. However, the approach could be easily extended to learn from existing optimal meshes if they are available, for instance when the computations use an adaptive approach to reach the required accuracy.

The methodology proposed in this paper is also assessed in terms of efficiency and the environmental implications. To this end, the carbon footprint and energy consumption of the computations required to perform a parametric CFD analysis of a wing for varying flow conditions and angle of attack is considered. The usual practice in industry consists of generating a fixed, very fine, mesh that is capable of capturing the flow features for all the configurations to be tested. This is usually done to minimise the required human intervention that is required to generate tailored meshes for each one of the cases of interest. With the approach proposed here, it is possible to obtain near-optimal meshes at a negligible cost, after a NN has been trained. However, in recent years there have been growing concerns about the lack of transparency when reporting the gains induced by the use of NNs [10]. This is due to the lack of data related to the cost of training and fine tuning the NNs that are subsequently used to perform accurate predictions. This work aims at reporting the full cost of the proposed approach by accounting for the fine tuning of the NN and even the repetition of experiments usually performed to minimise the effect of the randomness introduced in the initialisation of the NN weights.

Despite the use of machine learning algorithms in the computational engineering field has increased exponentially during the last years, the focus seems to be on learning to predict physical phenomena [11,12,13]. The use of machine learning to assist the mesh generation has attracted much less attention, but related work can be found in the literature. Early attempts to use NNs to predict the mesh density can be found in the framework of magnetic device simulations [14,15,16]. More recently, in [17, 18] the authors propose the use of a NN to predict the spacing at a given location based on some geometric parameters, boundary conditions and parameters of the partial differential equation under consideration. Algorithms based on NNs to assist mesh adaptive strategies have also been recently proposed [19,20,21] as well as the use of NNs to inform mesh adaptation in transient simulations [22] and even the assessment of mesh quality [23].

The approach proposed here is, to the authors knowledge, the first attempt to predict the mesh spacing function that is suitable for new simulations by using the flexibility of mesh sources. The potential of the proposed approach is demonstrated in the context of three dimensional inviscid compressible flows, but the strategy is general and does not rely on partial differential equations that describe the underlying physical phenomena. It is worth noting that the aim is to predict the mesh spacing and not the solution for two main reasons. First, the volume of data required to perform accurate predictions of three dimensional solutions of large scale problems could render such an approach unfeasible. Second, when utilising NNs to predict unseen cases, there is a level of uncertainty that is difficult to control. It is apparent that an error in the mesh spacing function is orders of magnitude more acceptable than errors in engineering quantities of interest. In fact, the near-optimal meshes predicted with the proposed approach can be further tuned using mesh adaptivity to ensure a reliable output to be used in engineering design.

The remainder of the paper is organised as follows. Section 2 summarises the required concepts on mesh spacing and control and neural networks. The proposed strategy is described in detail in Sect. 3, including the algorithms proposed for each one of the stages involved in the process. Numerical examples are presented in Sect. 4. The examples demonstrate the applicability and potential of the method in a CFD context, including problems with flow and geometric parameters. The predicted near-optimal meshes are assessed, not only by comparing the predicted spacing to the target spacing, but also by assessing the accuracy of the computed CFD solutions on the predicted meshes. Section 5 presents a detailed analysis of the efficiency of the method presented when compared to the current industrial practice and the environmental implications are discussed. Finally, Sect. 6 summarises the conclusions of the work that has been presented.

2 Background

This Section introduces some fundamental concepts on mesh spacing and neural networks that are utilised when presenting the proposed strategy to predict near-optimal meshes.

2.1 Mesh spacing and control

The ability of unstructured meshes to efficiently discretise complex geometric domains has made them the preferred choice in the aerospace industry for CFD simulations. In contrast to structured meshes, the efficiency arises from the ability of an unstructured mesh to locally refine regions of interest with minimal impact on the rest of the domain. Refinement techniques can be divided into, automatic based on mesh adaptivity, or manually controlled based on user expertise. Adaptive remeshing can be regarded as an automatic technique which can be used to concentrate elements in regions where the gradient of the solution is high. However, it is known that an inadequate initial mesh, despite many refinement loops, may result in some unresolved flow features.

Various techniques have been utilised to enable user-controlled refinement and to allow engineers to generate elements with the desired size in a given region of the domain. These techniques include the use of a background mesh, the use of points, lines or triangular sources and the refinement based on boundary curvature [5].

The requirement of manually generating a coarse mesh that covers the domain of interest, has restricted the use of background meshes in three dimensions. However, they are frequently used to control the gradation of the spacing between the region of interest and the rest of the domain. In this case, an unstructured mesh, made from a few tetrahedral elements, is manually created, and the desired spacing at the nodes of the mesh is defined. The spacing at any point in the domain is computed by using a linear interpolation of the nodal spacing values corresponding to the tetrahedron that contains the point.

Alternatively, sources provide flexible control of the local spacing desired at a given region. A point source defined, at a given location ${\varvec{x}}$, provides the required spacing $\delta _{0}$ at that location. The region of influence of the source is defined by specifying a sphere of radius r, within which the spacing remains constant. To avoid a sudden increase of the spacing beyond the sphere of influence, an exponential increase of the spacing is defined by providing a second radius, R, at which the spacing doubles. Hence, the spacing at a distance d, from the source location ${\varvec{x}}$, is given by

$$\begin{aligned} \delta (d) = {\left\{ \begin{array}{ll} \delta _{0} &{} \quad \text {if } d < r\\ \delta _{0}e^{\ln (2)\frac{d-r}{R-r}} &{} \quad \text {otherwise} \end{array}\right. }. \end{aligned}$$

(1)

The way a line source controls the local spacing is an extension of the point source. A line source is defined by connecting two point sources. The location of the nearest point on the line, ${\varvec{\hat{p}}}$, to a given point in space, ${\varvec{p}}$, is first determined. Using the two points of the line source, a linear interpolation is employed to determine the spacing and radii at ${\varvec{\hat{p}}}$. The location ${\varvec{\hat{p}}}$ is used as a point source with the interpolated spacing and radii and to determine the required spacing at the point ${\varvec{\hat{p}}}$. The extension to triangular sources follows the same rationale.

When multiple mechanisms are utilised to control the size of the elements, the minimum value of the spacing obtained from all mechanisms will be utilised during the mesh generation stage.

2.2 Artificial neural networks

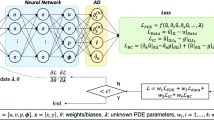
Artificial neural networks (NNs) are an assortment of neurons organised by layers. For the NNs considered in this work, each neuron is connected to all the neurons of the previous and subsequent layers. Each connection between the neurons has an associated weight, and each neuron has a bias. This particular case is referred to as a multi-layer perceptron, which is a class of feed-forward NNs. The first and last layers of the network are called input and output layers, respectively. The remaining layers, called hidden layers are numbered $l = 1,\ldots ,N_{l}$, with $N_{l}$ being the number of hidden layers [24].

During the forward propagation, the value of a neuron in the layer $l+1$ is computed by using the values associated with the neurons in the previous layer, l, the weights of the connections, and the bias from the previous layer, which is then modified by an activation function $F^{l}$. Mathematically, the value of the j-th neuron in the layer $l+1$, denoted by $z_{j}^{l+1}$, is computed as

$$\begin{aligned} z^{l+1}_{j} = F^{l+1} \left( \sum _{i=1}^{N^{l}_{n}}\theta ^{l}_{ij}z^{l}_{i} + b^{l}_{j} \right) , \end{aligned}$$

(2)

where $b^{l}_{j}$ is a bias that is introduced to enhance the approximation properties of the network, $\theta ^{l}_{ij}$ denotes the weight of the connection between the i-th neuron of the layer l and the j-th neuron of the layer $l+1$ and $N^{l}_{n}$ is the number of neurons in the layer l. An illustration of a generic multi-layer perceptron NN is shown in Fig. 1.

Fig. 1

Schematic representation of a multi-layer perceptron NN

For a single case with N inputs and M outputs, the NN has an input vector $\mathbf {x} = \{x_{1},...,x_{N} \}^T$, and an output vector $\mathbf {y} = \{y_{1},...,y_{M} \}^T$. As part of the training process, to determine how well a NN is performing in the prediction of the outputs, a cost function is used. The cost function used is constructed using the mean square error, that measures the discrepancy between the true outputs and the NN predictions. The cost function for $N_{tr}$ training cases is

$$\begin{aligned} C({\varvec{\theta }}) = \frac{1}{N_{tr}M} \sum _{k=1}^{N_{tr}} \sum _{i=1}^M [ y^k_i(x^k) - h_i^k({\varvec{\theta }}) ]^2, \end{aligned}$$

(3)

where $h_i^k({\varvec{\theta }})$ corresponds to the predicted output computed using the forward propagation.

The goal of the training stage is to minimise the cost function of Eq. (3), by optimising the weights and biases. The ADAM optimiser is employed in this work [25], which is considered computationally efficient and well suited for problems involving large data sets or a large number of parameters. The ADAM optimiser used to update a given weight at iteration $r+1$ in given by

$$\begin{aligned} \theta ^{l,r+1}_{i,j} = \theta ^{l,r}_{i,j} -\eta \frac{m^{l,r}_{i,j}}{\sqrt{v^{l,r}_{i,j}}+\epsilon }, \end{aligned}$$

(4)

where

$$\begin{aligned} m^{l,r+1}_{i,j} = \frac{\gamma _1(1-\gamma _1^{r-1})}{1-\gamma _1^r} m^{l,r}_{i,j} - \frac{1-\gamma _1}{1-\gamma _1^r}\frac{\partial C}{\partial \theta ^{l,r}_{i,j}} \end{aligned}$$

(5)

and

$$\begin{aligned} v^{l,r+1}_{i,j} = \frac{\gamma _2(1-\gamma _2^{r-1})}{1-\gamma _2^r} v^{l,r}_{i,j} - \frac{1-\gamma _2}{1-\gamma _2^r}\left( \frac{\partial C}{\partial \theta ^{l,r}_{i,j}} \right) ^2. \end{aligned}$$

(6)

In the above expressions, the step size is taken as $\eta =10^{-3}$, the exponential decays for the moment estimates are taken as ${\gamma _1=0.9}$ and $\gamma _2 = 0.999$, and the regularisation is taken as $\epsilon = 10^{-7}$.

The design of the NN considered in this work requires selecting an appropriate number of layers, number of neurons per layer and the activation function. The selection of the number of layers and neurons is done by studying the performance of the network for different values of these hyperparameters. Examples of these studies will be presented in the numerical examples in Sect. 4.

Numerical experiments have been performed to analyse the influence of the activation function on the predicting accuracy of the NN. The experiments showed that the sigmoid function produced more accurate results for reduced datasets, when compared to other classical activation functions. Therefore, the architecture selected involves the use of the sigmoid function for all hidden layers and a linear function for the output layer. These functions are given by

$$\begin{aligned} S(x) = \frac{1}{1+e^{-x}} \qquad \text {and} \qquad L(x) = x, \end{aligned}$$

(7)

respectively.

3 Construction of near-optimal meshes

To obtain an optimum engineering design, numerous geometric configurations must be analysed through the range of operating conditions. Reducing the time to generate a solution with the required accuracy enables more configurations to be evaluated. In addition, often, multiple meshes are required to ensure that the asymptotic convergence has been reached. This process has to be repeated for every configuration and for every operating condition. Alternatively, a fine mesh that is capable of capturing the features for a range of operating conditions can be used. The first process could either be automated, by using mesh adaptivity, or manually controlled, by enhancing and updating the parameters of the used mesh control technique.

This work proposes to use historic data, accumulated from analysis carried out during previous designs, to predict an appropriate starting mesh that can be considered as a near-optimal for a given geometric configuration and/or operating conditions. It is assumed that solutions satisfying the desired accuracy, for a range of geometric configurations and operating conditions, are available. These solutions could have been achieved utilising different modelling techniques, such as structured, unstructured or hybrid methods.

The proposed concept to generate a near-optimal mesh can be summarised in the following four stages:

• 1. For every solution, obtained from a given set of design parameters, create a set of point sources that can generate a mesh to capture the given solution.

• 2. Combine the individual sets of sources into a global set that is customised to generate the available mesh for all given cases.

• 3. Train a NN to predict the characteristics of the global set of sources for a new, unseen, set of input parameters.

• 4. Reduce the predicted global sources and combine point sources into line sources prior to generating the near-optimal mesh.

These four stages are described in detail in the remainder of this Section.

3.1 Generating point sources from a given solution

The process of creating a set of sources that leads to a mesh capable of capturing a given solution, requires the computation of the suitable element size at every point in space. Here, the element spacing is related to the derivatives of the solution using the Hessian matrix, a principle that is commonly used in error analysis, such as

$$\begin{aligned} \delta _\beta ^2 \, \left( \sum _{i,j=1}^N H_{ij} \beta _i \beta _j \right) = K, \end{aligned}$$

(8)

where ${\varvec{\beta }}$ is an arbitrary unit vector, $\delta _\beta$ is the spacing along the direction of ${\varvec{\beta }}$, $H_{ij}$ are the components of the Hessian matrix of a selected key variable $\sigma$, namely

$$\begin{aligned} H_{ij} = \frac{ \partial ^2 \sigma }{\partial x_i \partial x_j}, \end{aligned}$$

(9)

and K is a user-defined constant.

The derivatives of the key variable, $\sigma$, are computed, at each node of the current mesh, by using a recovery process, based upon a variational residual statement [26, 27]. Next, the optimal value of the spacing at a node is taken to be

$$\begin{aligned} \delta _i = \min _{i=1,\ldots , n} \left\{ \sqrt{ \frac{K}{\lambda _i}} \right\} , \end{aligned}$$

(10)

where $\lambda _i$, for $i=1, \ldots , n$, are the eigenvalues of the Hessian matrix, $\mathbf {H}$.

The spatial distribution of the mesh parameters is uniquely defined when a value for the user-defined constant K is specified. For smooth regions of the flow, this constant reflects the value of the root mean square error in the key variable that can be accepted.

In the current implementation, two threshold values for the computed spacing are used: a minimum spacing $\delta _{min}$ and a maximum spacing $\delta _{max}$, so that

$$\begin{aligned} \delta _{min} \le \delta _i \le \delta _{max}, \quad \mathrm{for} \quad i=1,\ldots , N. \end{aligned}$$

(11)

The reason for defining the maximum value, $\delta _{max}$, is to account for the possibility of a vanishing eigenvalue in Eq. (10). The value of $\delta _{max}$ is chosen as the spacing to be used in the regions where the solution is smooth. On the other hand, maximum values of the second derivatives occur near regions with steep gradients, where the gradient demands that smaller elements are used. By imposing a minimum value for the mesh size, $\delta _{min}$, an excessive concentration of elements near regions with steep gradients is avoided.

To enable the use of data that was generated using different numerical techniques, a method which ensures the uniformity of the training data has to be devised. Since the underlying meshes that were used for generating the data can be different and are often very large, the use of sources to specify the mesh requirement to capture the given solutions is proposed.

The main idea is, for a given mesh, to group points that have similar required spacing, calculated using Eq. (10), to form a point source that is located at the centre of the grouped points with a radius that extend from the centre to the furthest point in the group. This process reduces the quantity of information needed to describe an optimal mesh by up to two orders of magnitude, without sacrificing the quality of the information which describes the required mesh.

It is worth noting that the process will reflect the level of fidelity provided by the given solutions. Hence, the process can be used both, at the initial investigation stage, when the meshes are not highly refined, and at the data acquisition stage, when the solutions are provided on a highly refined mesh or on an adapted mesh.

Algorithm 1 describes the devised technique to convert a given solution to a set of point sources.

The process starts from the computed spacing required at every point of the mesh to capture a given solution. To ensure optimum grouping of points that have similar required spacing, the number of surrounding layers of nodes with spacing similar to the node under consideration is computed. Figure 2 illustrates the concept of surrounding layers.

Fig. 2

Detail of a triangular mesh illustrating the concept of surrounding layers. The central node is denoted by a blue star. The nodes with similar spacing are denoted with a green circle, whereas nodes with a dissimilar spacing are denoted with a red triangle. The scenario in a shows one surrounding layer of nodes with similar spacing to the central node, whereas the scenario in b shows two surrounding layers

The process ensures that the spacing required at every node of the given mesh is covered by a minimum of one point source. In the current implementation, it is assumed that the radius R, where the spacing doubles, is twice the radius r where the spacing is constant and equal to the spacing of the grouped points. It is also assumed that different spacings are similar, if they are lower than $5\%$ of the spacing at the node under consideration. The creation of a point source is terminated if the spacing at a surrounding layer is larger than the spacing at the radius R of the point source.

3.2 Generating global sources from sets of local sources

The process described above does not guarantee that the number of sources to capture the required meshes is the same, for different sets of input parameters. In addition, despite the fact that two sets of sources would contain sources in close proximity, their position in the list of sources can be, in general, very different. The former will make the use of NNs unfeasible, whereas the later will impose significant difficulties when finding a correlation between inputs and outputs. To solve these two issues, a process to create one set of global sources that can be used for all sets of input parameters is devised.

The basic idea is to create one set of global sources which can be used to map the index of each source in a local set to an index of a source in the global set. The mapping is based on the minimum distance between the global and local sources and it is defined as

$$\begin{aligned} \begin{aligned} \mathcal {F}\; : L&\longrightarrow G \\ (j,i)&\longmapsto \mathcal {F}(j,i):= {\left\{ \begin{array}{ll} k \qquad \text { if } \exists k \in G \text { |} \lambda _{j,i} = \Lambda _k \\ 0 \qquad \text { otherwise } \end{array}\right. }, \end{aligned} \end{aligned}$$

(12)

where $L_i = \{ (j,i) \; \text {|} \; j\in \{1,\ldots , \text {|} \mathcal {S}_i \text {|} \}\}$ denotes the indices of local sources in $\mathcal {S}_i$, the indices of all local sources is $L=L_1 \cup \ldots \cup L_C$ and the indices of the global sources is $G = \{1, \ldots , \text {|} \mathcal {G} \text {|} \}$, where $\mathcal {G}$ is the list of global sources.

Algorithm 2 describes the developed process to combine the sets of local sources into one set of global sources. The set of global sources are further tuned for each input set of parameters to produce the required mesh to capture the given solution.

The process starts with an empty list of global sources and considers one case at a time. As the sources of the first available case are unique, they are added to the list of global sources with a one to one mapping. Any newly added source to the global list is inserted in an ADT data structure. The ADT is then be utilised to identify sources from the global list that are in close proximity to the remaining local sources. If no source from the global list is close to a local source, the local source is added to the list of global sources and the mapping is updated. If a global source is found to be in close proximity of a local source, the local source index is mapped to the global source index. When all cases are considered, the global set of sources are customised for each set of input parameters. For each case, if a local source has been mapped to a global source, the local source characteristics are used unchanged. For any global source that has no corresponding local source, the characteristics are calculated to ensure that the spacing produced is compatible with the spacing that would be produced by the local source.

Figure 3 illustrates the two algorithms described above using a two dimensional example with two design variables, namely the free-stream Mach number and the angle of attack. For each training case, the pressure field is used to obtain a set of point sources. The point sources in Fig. 3 are represented by circles, coloured using the spacing value and with a radius proportional to the radius of influence of each source. The illustration, made with real data from a two dimensional example, shows that point sources with small spacing are created in the regions where the solution shows a high pressure gradient.

Fig. 3

Illustration of the process described in Algorithms 1 and 2 to obtain the point sources for a set of training cases and the construction of the global set of sources

Once the point sources for all cases are constructed, the sets of global sources are created for each case using Algorithm 1. This process ensures that the number of global sources is the same in all cases, and therefore the data can be used to train a NN.

3.3 Construction of NN for predicting the characteristics of the sources

The creation of a set of global sources, with the same number of characteristics for all cases, enables the use of NNs to predict these characteristics for unseen cases. In this work, the objective is to predict the location, spacing and the radius within which the spacing remains constant. Generally, the values of the spacing and the radius varies by more than two orders of magnitude. To ensure a consistent training of the NN, without a bias towards larger values, the logarithm of the spacing and the radius is used. This scaling also prevents the NN predicting unrealistic negative values for these two outputs.

As stated in Sect. 2.2, the NN has an input input vector ${\mathbf {x} = \{x_1,...,x_N \}^T}$, and an output vector $\mathbf {y} = \{y_1,...,y_M \}^T$. In the numerical examples considered in this work, the number of inputs, N, is related the flow conditions and/or geometric parameters, whereas the number of outputs M are the source characteristics (i.e., position, spacing and radius r). When $N_{tr}$ training cases are considered, the input is an array of size $N \times N_{tr}$ and the output is an array of size $M \times N_{src} \times N_{tr}$, where $N_{src}$ is the number of global sources.

Different models can be used to train and predict the characteristics of the global sources. The obvious choice is to train one NN to predict all the source characteristics. However, this work will also investigate the use of different NNs to train source characteristics of different nature. For instance, one NN can be trained to predict the position of the sources, another NN to predict the spacing and another NN to predict the radius. Another alternative would be to train $N_{src}$ NNs, each one trained to predict the characteristics of a single source.

In terms of the implementation, TensorFlow 2.7.0 [28] was used to construct the NNs considered in this work. To ensure that the NN prediction capability is not heavily influenced by the initial choice of the NN weights, the training is performed five times for each experiment considered by varying the seed values of the optimisation process. For each training, a maximum of 500 epochs is considered and the training is stopped when either the maximum number of epochs is reached or no improvement in the objective function is observed during 50 consecutive epochs. It is worth noting that the batch size used in all the examples considered is eight, which for the examples presented here produced a better performance than the default value of 32 in TensorFlow.

To measure the accuracy of the NN predictions, the classical statistical R$^2$ measure [29] is considered for all the test cases. To better illustrate the difficulty on predicting the different characteristics of mesh sources, the R$^2$ measure is reported for the five characteristics independently (x, y and z position of the source, spacing and radius).

3.4 Reducing the global set of sources

After the training stage, a NN is used to predict the characteristics of the global set of sources for unseen cases. Although it is possible to use the global set of sources to generate a predicted mesh, removing from the list of global sources entries that are redundant, has the potential to speed up the generation process considerably. This is because, during the mesh generation process, it is necessary to compute the spacing induced by each source at a point to take the minimum of all the spacings.

Sources with an associated spacing function adequately described by other sources are classed as surplus. Algorithm 3 describes the process devised to remove surplus sources.

The algorithm starts by determining the maximum region of influence of each source, i.e. the region where the computed spacing from the source reaches the maximum allowable spacing. All sources are inserted into an ADT data structure to speed up the search process. For each source in the global list, the ADT is searched to identify sources that have an overlapping sphere with the source under consideration. The source with a larger spacing is removed if its associated sphere is inside the associated sphere of the source with smaller spacing.

A further check is conducted to determine if the region of influence of a source can be covered by multiple regions of influence of other sources. This is performed in a discrete fashion, by using the spacing of the source to divide the region of influence of the source under consideration into a uniform local grid. The spacing at each point of the local grid is evaluated using the sources that have been already added to the list of reduced sources. If the evaluated spacing at any point of the local grid has a larger spacing that the spacing from the source under consideration, the source is added to the list of reduced sources.

Figure 4 illustrates the on-line stage of the proposed approach. After the NN is trained, for a new set of design parameters (flow conditions in this two dimensional example), the NN is used to predict the characteristics of the global sources. Using Algorithm 3, the sources are reduced. This process ensures that the mesh generation stage does not require a very large number of queries to compute the spacing at a point. For the examples considered in this work, Algorithm 3 produces a reduction of around 60% in the number of point sources.

Fig. 4

Illustration of prediction stage using the trained NN and the process described in Algorithms 3 to reduce the set of sources before generating and mesh that can finally be used to compute a solution

Once the mesh is obtained, the standard CFD calculation is performed. The illustrative example of Fig. 4 shows the computed pressure field, which exhibits all the expected flow features for this transonic case.

In an attempt to produce a smooth spacing function, line sources are created using a group of point sources. Algorithm 4 describes the process that is proposed for the creation of line sources from grouped point sources. An iterative process is used to identify sources that have similar spacing and their associated sphere intersects with the associated sphere of a source that has already been added to the group. Orthogonal regression is then used to fit a plane to the grouped point sources. The distance of each point source to the plane is calculated, and the points with a distance greater than their radius of influence are removed from the group. The process of finding a best fit plane continues until all points in the group are within the allowable distance. The coordinates of the remaining point sources are projected onto the best fit plane and used to compute the best fit line using orthogonal regression. The process of removing points from the group that do not satisfy the allowable distance criteria will also be applied to the projected points. The furthest two points remaining in the group will be used to form a line source.

4 Numerical examples

This Section presents three numerical examples of increasing difficulty to test the potential and applicability of the proposed technique. The examples involve the prediction of meshes for three dimensional CFD simulations involving inflow conditions and geometric parameters. One of the challenges of the examples used is that the variation of the input parameters induce different flow patterns that include subsonic and transonic cases with different shock structures and strength. Therefore, being able to predict the near-optimal mesh for unseen cases is not an easy task.

4.1 Near-optimal mesh predictions on the ONERA M6 wing at various inflow conditions

The first example considers the prediction of near-optimal meshes over a fixed geometry, with variable flow conditions. The objective is to study the potential of the proposed approach to accurately predict the sources that can be used to generate near-optimal meshes for unseen flow conditions. Numerical experiments are used to study the influence of the hyperparameters and the size of the training set.

The geometry used in this example is the ONERA M6 wing [30] and the inviscid compressible flow conditions are described by two parameters, namely the free-stream Mach number, $M_\infty$, and the angle of attack, $\alpha$. It is worth noting that the range used for the parameters, $M_\infty \in [0.3,0.9]$ and $\alpha \in [0^\circ ,12^\circ ]$ leads to subsonic and transonic flows. This means that the required meshes vary substantially with respect to the flow conditions.

To illustrate the variation in the solution induced by the parameters, Fig. 5 shows the pressure coefficient, $C_p$, for three different combinations of the input parameters. For the first set of input parameters, $M_\infty =0.41$ and $\alpha =8.90^\circ$, the flow is subsonic and the mesh should be refined near the leading and trailing edges to capture the high variation of the pressure on these regions. For the second set of inputs, $M_\infty =0.79$ and $\alpha =5.39^\circ$, the typical $\lambda$-shock can be clearly observed. Refinement near the discontinuity of the pressure is therefore necessary to capture such abrupt changes in the pressure field. Finally, for the last set of inputs, $M_\infty =0.80$ and $\alpha =8.19^\circ$, the $\lambda$-shock is also clearly visible, but at a different position and with a different strength when compared to the second case. The simulations were performed using the in-house flow solver FLITE [31] with unstructured tetrahedral meshes consisting of approximately 1.3 M elements and 230K nodes. The surface mesh is made of approximately 20K triangular elements.

Fig. 5

Pressure coefficient, $C_p$, for three different flow conditions

For training, a set with $N_{tr}=160$ cases is considered and a set with $N_{tst}=100$ cases is considered for testing. To minimise the undesired use of the trained NNs for extrapolation, the training set is generated in the region of interest, namely $(M_\infty ,\alpha ) \in [0.3,0.9] \times [0^\circ ,12^\circ ]$, whereas the test set is generated using a reduced space, namely $(M_\infty ,\alpha ) \in [0.33,0.81] \times [1.0^\circ ,11.0^\circ ]$. Both the training and testing datasets are displayed in Fig. 6.

Fig. 6

Data sets for training (blue circles) and testing (red crosses) for the example with varying flow conditions

To produce sampling points that offer good coverage of the parametric space, the training and testing datasets are generated using scrambled Halton sequencing. The Halton sequence is a sequence of points commonly used in numerical analysis and Monte Carlo simulations because it is deterministic and the points generated have low discrepancy [32]. The scrambled Halton sequence is a modification of the original Halton sequence to improve performance in higher dimensions [33, 34].

It should be noted that when utilising data generated by industry over the years, the training set will most likely not correspond to a Hatlton sequencing. It would be expected that the cases available have been decided by an expert engineer and, therefore, would be specifically selected to capture sensitive areas of the flight envelope that undergo large changes in flow features. Such bias in parameter selection is expected to improve the accuracy of the NNs. As such, the random approach of the Halton sequencing taken in this paper is a more conservative approach that requires more training data.

The number of sources generated from the solutions of the training and test datasets, computed using Algorithm 1, varied between 2142 and 5593. The global set of sources that resulted from the combination of sources described in Algorithm 2 and used for training the NNs consisted of 19,345 sources.

Three different models could be used for predicting the characteristics of the sources. All the models use the same two inputs, but differ by the number of NNs required and the number of predicted outputs for each NN. The first model predicts the five characteristics of all the sources using a single NN. The second model trains the location (three coordinates) of all the sources using one NN, whereas the spacing and radius are trained using two more NNs. The third model trains each characteristic of all the sources separately, requiring the training of five NNs. The three models under consideration are summarised in Table 1.

Table 1 Three models used for training NNs able to predict the characteristics of the sources

Three further models could be considered, where the training of each source is performed independently. For instance, $N_{src}$ NNs could be trained to predict the five characteristics of each source. Similarly, three NNs could be trained per source or even five NNs per source. These three models are not considered in the current work because they become impractical for realistic problems involving a large number of sources. Not only the training requires the construction of thousands of NNs, but also the prediction stage requires loading the weights of thousands of NNs to compute the required spacing.

To compare the three models described in Table 1, first the hyperparameters of each NN are tuned. Figure 7 shows the variation of the R$^{2}$ as a function of the number of layers and the number of neurons in each layer when using $N_{Tr} = 160$ training cases. It is worth noting that a different colour scale is used for the coordinates and the remaining two characteristics, i.e. spacing and radius. The results show that it is substantially more difficult to predict the spacing and radius, compared to the coordinates of the source. In addition, the accuracy of the predicted coordinates is almost insensitive to the NN architecture, whereas the spacing and radius benefit from using a particular choice of hyperparameters. The most suitable architecture for this example would be a NN with three hidden layers and 25 neurons per layer. This will provide the best possible accuracy for all the characteristics whilst minimising the size of the NN.

Fig. 7

r$^{2}$ for the five source characteristics as a function of the number of layers and number of neurons in each layer for model 2 and for the example with varying flow conditions

Figure 8 shows the regression plot for the spacing, for three flow conditions that correspond to a subsonic and two transonic cases. It is worth noting that the R$^2$ value for all cases is above 90, despite the substantial difference in flow features between a subsonic and a transonic case. This shows the robustness of the proposed approach when predicting the spacing of each source, which is the most difficult quantity to predict accurately.

Fig. 8

The regression plots for the spacing, $\delta _0$, for three flow conditions corresponding to a subsonic and two transonic cases

The histogram in Fig. 9 shows the R$^{2}$ for all test cases. The results show that only one test case has an R$^{2}$ value below 90 and the average R$^{2}$ is above 96. This demonstrates the accuracy of the predictions for unseen cases encompassing both subsonic and transonic flow features.

Fig. 9

R$^{2}$ histogram for all test cases for the example with varying flow conditions

The next experiment aims to investigate the influence of the number of training cases, $N_{tr}$, in the accuracy of the predictions and the performance of the three models described in Table 1. Figure 10 shows the minimum R$^2$ for the five mesh characteristics as a function of the number of training cases, for the three models of Table 1. The minimum number of training cases used was 10, and it was increased until the total number of available cases was selected. All the test cases were used in assessing the accuracy of the selected NN regardless of the number of training cases used. For each number of training cases, the hyperparameters were tuned, as presented earlier.

Fig. 10

Minimum R$^2$ for the five mesh characteristics as a function of the number of training cases for the three models of Table 1

The results show that very few training cases are required to perform accurate predictions of the coordinates of the sources. This is expected because, as explained in Sect. 3.2, sources are grouped based on proximity. The prediction of the spacing and radius is much more challenging and the results show that models 2 and 3 are able to outperform model 1. This is because both models 2 and 3 train an independent NN to predict the spacing and radius, whereas in the first model, a single NN is used to predict all characteristics. The performance of models 2 and 3 is almost identical.

To illustrate the potential of the proposed approach, the trained NNs are next used to predict the characteristics of the sources and near-optimal meshes are generated and compared with target meshes. All the meshes are generated following the process to eliminate surplus point sources described in Algorithm 3. In addition, point sources are merged into line sources using Algorithm 4.

Figure 11 shows the target mesh and the predictions using the three models of Table 1. The flow conditions corresponds to $M_\infty = 0.79$ and $\alpha = 5.39^\circ$. The meshes produced with the three models exhibit the refinement required to capture the most important features of this transonic flow. However, model 1 predicts a larger spacing near the location of the shock, whereas the characteristics of the sources produced by models 2 and 3 produce a spacing much more similar to the target. It is worth noting that the only difference between models 2 and 3 is the prediction in the location of the sources. It is expected that the position of the sources is more accurate in model 3 because independent NNs are used for each one of the three coordinates. However, the gain is expected to be negligible because the previous experiments showed that the location of the sources is the easiest quantity to predict, even when using a very reduced training set.

Fig. 11

Target mesh and predicted meshes using the three models of Table 1 for $M_\infty = 0.79$ and $\alpha = 5.39^\circ$

To further illustrate the performance of each model, the spacing function induced by the predicted sources is compared with the spacing function induced by the target sources. To this end, the spacing induced by the predicted sources is compared to the target spacing at the centroid of each element of the target mesh, for all test cases. Figure 12 shows the histogram of the ratio between predicted and target spacing for the three models. The minimum and maximum values for each bin in the histogram are depicted with red error bars, whereas the orange bar represents the standard deviation from the mean. A value of the ratio between 1/1.25 and 1.25 is considered extremely accurate and it should produce a mesh able to capture all the targeted flow features. Values of the ratio higher than 1.25 indicate that there are regions where the NN predicts a larger spacing, resulting in an under-refined mesh that can lead to missing some flow features. Similarly, a value of the ratio below 1/1.25 indicates that there are regions where the NN predicts a smaller spacing, resulting in regions unnecessarily refined.

Fig. 12

Histogram of the ratio between the predicted and target spacing for the three models of Table 1

The results in Fig. 12 show a very similar performance of the three models. Model 1 exhibits a slightly lower value in the middle bin, whereas the bin between 1.15 and 1.25 contains a larger percentage of elements when compared to models 2 and 3. It can also be observed that the worst performing case for model 1 is less accurate than the worst case produced from models 2 and 3. The performance of models 2 and 3 is very similar, with a marginal better performance provided by model 3.

Using the best available NN in model 3, the predicted sources for the three test cases are used to produce the near-optimal meshes for the cases shown in Fig. 5. Figure 13 shows the target and predicted meshes for three different flow conditions. The results clearly show the ability of the proposed technique to produce meshes that are locally refined near the relevant regions, with no manual interaction and no required user expertise.

Fig. 13

Target (top row) and predicted (bottom row) meshes using model 2 for three flow conditions

The solutions obtained using the predicted near-optimal meshes are shown in Fig. 14. To further compare the accuracy of the solutions obtained on the predicted near-optimal meshes, Fig. 15 compares the pressure coefficient, at one section of the wing, to the pressure coefficient computed with the target mesh. The results indicate that, regardless of the flow regime, the resolution of all flow features are captured equally well by the meshes generated using the predicted and target sources.

Fig. 14

Pressure coefficient, $C_p$, for three different flow conditions, computed using the predicted near-optimal meshes of Fig. 13

Fig. 15

Comparison of the pressure coefficient, $C_p$, for three different flow conditions, at one section

Finally, the lift, $C_L$, and drag, $C_D$, coefficients obtained from the simulations using the meshes generated from the target sources and the meshes generated from the predicted sources are compared in Table 2. A maximum difference of two lift counts and two drag counts, further confirms the ability of the trained sources to construct the required meshes for unseen cases.

Table 2 Comparison of the aerodynamic coefficients computed with the target and predicted meshes for three flow conditions

An alternative approach to using a NN to predict a near-optimal mesh for an unseen test case would be to use an optimal mesh from a similar flight condition from the training dataset. A case from the unseen test set is selected to compare this alternative method with the NN approach presented in this paper. The case used is a transonic case, where the optimal mesh varies significantly as the parameters change, and the accuracy of the solution is very sensitive to using an appropriate mesh.

Taking an example flight condition of $(M_\infty ,\alpha )$ being $(0.79, 5.39^\circ )$, above, the nearest training cases in the parametric space corresponds to $(M_\infty ,\alpha )$ equal to $(0.82, 5.34^\circ )$. Taking the optimal mesh from the training case and using it on the unseen test flight condition, a solution using the given mesh is obtained.

Comparing the lift, $C_L$, and drag, $C_D$, coefficients obtained using the two methods, a very large difference is found between the expected target results and the obtained results using a mesh from a similar case. The difference being 8 lift counts and 12 drag counts, which is beyond what is to be tolerated. Whereas the NN could accurately predict a mesh able to capture the solution within one lift and drag count of the target solution.

4.2 Near-optimal mesh predictions on a variable wing geometry at fixed inflow condition

The second example involves the prediction of near-optimal meshes for a geometrically parametrised wing at a fixed transonic condition of $M_\infty =0.85$ and $\alpha =3^\circ$. The geometry is constructed from two different four-digit NACA aerofoils placed at the root and the tip of the wing. A linear variation of the geometry is considered in the span direction of the wing. The three parameters of each four-digit NACA aerofoil form the input of the NN. Given the better performance of the model 3 architecture demonstrated in the previous example, this and the following example in Sect. 4.3, only use this model type for the NNs.

Halton sequencing of the six input parameters is used to generate a training dataset consisting of $N_{tr}=160$ training cases. For both aerofoils, the range of the maximum camber, m, is taken between 0 and 6, the range of location of the maximum camber, n, is set between 0 and 4 (corresponding to $0\%$ and $40\%$ of the chord) and the range of the thickness, p, is set between 6 and 24. A further dataset of $N_{tst}=40$ test cases is also generated using Halton sequencing. As in the previous example, the range of inputs used to generate the test cases is slightly modified to minimise the undesired use of the trained NNs for extrapolation. To illustrate the training and test datasets employed, Fig. 16 displays a histogram of the two datasets.

Fig. 16

Histograms of the sampling data used for the training and test sets of the variable wing geometry

For each training and test case, the CFD solution is obtained using FLITE [31] on an unstructured tetrahedral mesh consisting of approximately 1.3 M elements and 250K nodes. Figure 17 shows the pressure coefficient, $C_p$, on the surface and a cut across the wing for three geometries from the test set. The number of sources generated from the solution of each case in the datasets, based on Algorithm 1, varied between 3,949 and 7,571. The global set of sources that resulted from the combination of sources described in Algorithm 2, and used for training, consisted of 48,503 sources.

Fig. 17

Pressure coefficient, $C_p$, for three different geometric configurations. For each case the first NACA corresponds to the root of the wing and the second NACA corresponds to the tip

Following the rationale of the previous example, the influence of the number of training cases on the accuracy of the predictions is studied. For each number of training cases, the NN architecture is tuned by varying the number of hidden layers and neurons in each layer. Figure 18 shows the minimum R$^2$ for the five mesh characteristics as a function of the number of training cases. Similar to the previous example, predicting the coordinates of the sources requires very few training cases to achieve an excellent predicting accuracy. Predicting the spacing and radius of the sources is more difficult, but with 40 training cases the lowest R$^2$ is already above 80. It is worth noting that the same level of R$^2$ achieved in the first example is not reached. This is mainly attributed to the fact that in both cases the maximum number of training cases is 160 but this example contains three times more parameters. In addition, it is worth noting that the parameters considered in this example are geometric parameters and it is usually more difficult to generate reduced order models, when compared to flow conditions [12, 35].

Fig. 18

Minimum R$^2$ for the five mesh characteristics as a function of the number of training cases for the example with varying geometry

To quantify the ability of the model to predict the correct characteristics of the sources that produces a mesh comparable to the target mesh, the ratio between the spacing computed using the predicted sources and the target sources at the centroid of the elements was evaluated. Figure 19 shows the histogram of the ratio between predicted and target spacing. The results show that, despite the reduced size of the training dataset, less than 5% of the elements generated for all test cases have a spacing more than double the target spacing. The results suggest that more training cases that better sample the parametric space are needed. This can be achieved using a more generic definition of the geometry and eliminating the need to have the NACA digits as integer values.

Fig. 19

Histogram of the ratio between the predicted and target spacing for the example with varying geometry

Using the best available NN, the predicted sources are used to produce the near-optimal meshes for the three test cases outlined in Fig. 17. Figure 20 shows the target and predicted meshes for the three different geometric configurations. Despite the low number of training cases used for this problem involving six geometric parameters, the proposed approach is able to predict near-optimal meshes, capturing the local refinement required for different geometric configurations. It is worth noting that the last geometric case considered in Fig. 20 corresponds to a point near the boundary of the six-dimensional parametric space and therefore the accuracy of the prediction is expected to be lower, when compared to other cases.

Fig. 20

Target (top row) and predicted (bottom row) meshes for three geometric configurations

The solutions obtained using the predicted near-optimal meshes are shown in Fig. 21. To better compare the accuracy of the solutions obtained on predicted near-optimal meshes, Fig. 22 compares the pressure coefficient, at one section of the wing, with the pressure coefficient computed with the target mesh. The comparison of pressure coefficients shows that, despite some differences that can be observed on the predicted meshes of Fig. 20, the predicted near-optimal meshes are capable of capturing all the flow features. To confirm this finding, the lift, $C_L$, and drag, $C_D$, coefficients obtained from the simulations using the meshes generated from the target sources and the meshes generated from the predicted sources are compared in Table 3. A maximum difference of only three lift counts and two drag counts, confirms the ability of the trained sources to construct the required meshes for unseen cases.

Fig. 21

Pressure coefficient, $C_p$, for three different geometric configurations, computed using the predicted near-optimal meshes of Fig. 20

Fig. 22

Comparison of the pressure coefficient, $C_p$, for three different geometric configurations, at one section

Table 3 Comparison of the aerodynamic coefficients computed with the target and predicted meshes for three geometric configurations

4.3 Near-optimal mesh predictions at various inflow conditions on a variable wing geometry

The last example involves the prediction of near-optimal meshes for a geometrically parameterised wing at variable flow conditions. The geometry is the same used in the example of Sect. 4.2, whereas the flow conditions consider a Mach number and angle of attack between [0.6, 0.9] and $[-4^\circ , 10^\circ ]$, respectively.

A Halton sequencing of the six geometric parameters is used to generate a dataset consisting of 52 cases. For each value of the geometric parameters, a Halton sequencing of the two flow parameters was used to generate a dataset that consisted of 24 cases. The combination of the two datasets provides the final dataset that consisted of $N_{tr} =52 \times 24 = 1,248$ training cases. The same procedure was used to generate a test dataset that contains $N_{tst}=8 \times 24=192$ cases.

For each case in the training and test datasets, the solution is obtained using the FLITE [31] solver and an unstructured tetrahedral mesh consisting of approximately 1.3 M elements and 250K nodes. The distribution of the pressure coefficient for three test cases is shown in Fig. 23.

Fig. 23

Pressure coefficient, $C_p$, for three different geometric configurations and flow conditions. For each case the first NACA corresponds to the root of the wing and the second NACA corresponds to the tip

The number of sources generated from the solution of each case in the datasets, based on Algorithm 1, varied between 1,533 and 7,582. The global set of sources that resulted from the combination of sources described in Algorithm 2, and used for training, consisted of 54,713 sources. The influence of the number of training cases in the accuracy of the predictions is studied next. To better understand the importance of the flow and geometric parameters separately, the increase of the number of training cases is performed in three different ways. First, the number of training cases are increased by increasing only the number of geometric configurations, starting with 3 cases and doubling the number of geometric cases until all geometric configurations available are considered. For each geometric configuration, the 24 available flow conditions were used. Second, the number of training cases are increased by increasing only the number of flow conditions considered. Finally, the increase in the number of training cases is performed by not distinguishing the type of parameters, so increasing both the number of flow conditions and geometric configurations is considered.

Figure 24 shows the minimum R$^2$, for the five mesh characteristics, as a function of the number of training cases. The qualitative behaviour is similar to the previous examples. With a very reduced dataset for eight parameters, it is possible to produce very accurate predictions of the coordinates of the sources, whereas accurate predictions of the spacing and radius require a significant increase in the number of training cases. For a given number of training cases, the best NN architecture was found by varying the number of hidden layers and neurons in each layer, following the same process described in previous examples.

Fig. 24

Minimum R$^2$ for the five mesh characteristics as a function of the number of training cases for the example with varying flow conditions and geometry. Three different strategies of increasing the number of training cases are considered

To quantify the ability of the model to predict the correct characteristics of the sources that produces a mesh comparable to the target mesh, the ratio between the spacing computed using the predicted sources and the target sources at the centroid of the elements of the target mesh is evaluated. Figure 25 shows the histogram of the ratio between predicted and target spacing. Despite the larger number of parameters and the different nature of the parameters involved, the results show that less than 5% of the elements generated for all test cases have a spacing more than double the target spacing.

Fig. 25

Histogram of the ratio between the predicted and target spacing for the example with varying flow conditions and geometry

Using the predicted characteristics of the sources, meshes for the three test cases shown in Fig. 23 are produced, and compared to the meshes obtained with the target characteristics. As in the previous examples, all the meshes are generated following the process to eliminate surplus point sources described in Algorithm 3 and merging point sources into line sources using Algorithm 4. Figure 26 shows the target and predicted meshes for the three different geometric configurations. The results show that the proposed approach is able to predict the characteristics of the sources in such a way that the generated meshes provide appropriate mesh resolution near the regions where is needed. The smoothness of the spacing function in the second and third test cases of Fig. 26 could be improved by increasing the number of training cases or by modifying the similarity tolerance used for grouping sources.

Fig. 26

Target (top row) and predicted (bottom row) meshes for three flow conditions and geometric configurations

To analyse the ability of the near-optimal meshes generated to capture the required flow features, Fig. 27 shows the pressure coefficient distribution obtained with the predicted meshes of Fig. 26. To better quantify the accuracy of the solutions obtained on predicted near-optimal meshes, Fig. 28 compares the pressure coefficient, at one section of the wing, with the pressure coefficient computed with the target mesh. It can be clearly observed that despite the lack of smoothness in the spacing functions obtained with the predicted characteristics of the sources, the near-optimal meshes are able to correctly capture all the required flow features, offering an excellent agreement with the solutions computed on the target meshes.

Fig. 27

Pressure coefficient, $C_p$, for three different flow conditions and geometric configurations, computed using the predicted near-optimal meshes of Fig. 27

Fig. 28

Comparison of the pressure coefficient, $C_p$, for three different flow conditions and geometric configurations, at one section

Finally, the lift and drag coefficients resulted from the simulation using the mesh generated from target sources and the mesh generated from the predicted sources are compared in Table 4. A maximum difference of only one lift count and four drag counts confirms the ability of the trained NNs to predict the characteristics of the mesh sources for unseen cases.

Table 4 Comparison of the aerodynamic coefficients computed with the target and predicted meshes for three geometric configurations

5 Efficiency and environmental implications

The strategy proposed in this work relies on training a relatively large number of NNs using deep learning. The accuracy of the predictions has been evaluated and the implications in terms of reducing the number of hours required to produce near-optimal meshes for simulation are clear. However, in the last few years there have been growing concerns about the environmental impact of training large models using NNs [10, 36]. This is because the majority of articles found in the literature tend to focus on the accuracy of the predictions, but ignore the resources required to train and tune the NNs.

This Section aims at analysing the efficiency of the proposed approach to demonstrate that the strategy presented can be labelled as Green AI research [10], in the sense that it reduces the computational cost that is currently required in industry to achieve similar results.

When considering the computational and environmental impact of a methodology based on deep learning, several factors must be taken into consideration. These factors include not only the training time for one model, but also the time required to perform the hyperparameter tuning. In addition, other factors such as the computing infrastructure used, the hardware architecture or even the geographical location of the high performance computing (HPC) facilities employed [36, 37].

In this work, the model developed in [36] to estimate the carbon footprint of a computation is considered. The characteristics of the HPC facilities used in all the computations presented in this work are summarised in Table 5. The algorithms involved, when measuring the efficiency of the proposed approach, are the mesh generation algorithm, the CFD solver and the NN training. The mesh generator runs on a single processor. The CFD solver runs on 24 processors for meshes between 5 M to 6.5 M elements and on 64 processors for a mesh of 40 M elements. Finally, the training of the NN is performed using a single processor.

Table 5 Details of the algorithm and HPC facilities used

To analyse the efficiency and environmental impact of the methodology proposed in this work, the common task of performing CFD computations for a varying free-stream Mach number and angle of attack is considered. This corresponds to the first example described in Sect. 4.1. The free-stream Mach number varies between 0.3 and 0.9, and computations are performed in steps of 0.05. The angle of attack varies between $-4^\circ$ and 12$^\circ$, and computations are performed in steps of 1.6$^\circ$. This means that a total of 143 CFD computations are required.

The most common approach considered in industry when performing this parametric study consists of generating a fixed, very fine, mesh that is capable of capturing the solution for all the cases of interest [38]. This is done in practice to minimise the time consuming task of generating a mesh tailored for every single case, which is not only difficult, but actually requires a significant amount of human intervention. For the example considered here, an unstructured mesh of 40 M tetrahedral elements is generated. A detailed view of the fine mesh generated is shown in Fig. 29. The generation of this mesh takes only one hour on a single processor. However, the implications of generating a single mesh are substantial when running the CFD solver. In this example, each CFD simulation takes 24 h using 64 processors, which implies a server memory capacity of 192GB. This amounts for a total of 3,432 h to compute the 143 solutions required.

Fig. 29

Fine mesh around the M6 wing

Table 6 summarises the carbon footprint and energy consumption induced by the process of computing the 143 solutions with a fixed mesh. The footprint is obviously dominated by the CFD calculations and the total amount is equivalent to more than 3000 km in a passenger car, or almost a flight from New York City to San Francisco [36].

Table 6 Carbon footprint and energy consumption for the parametric study using a fixed mesh capable of accurately capturing all the solutions

The alternative, proposed in this work, is to train a NN with all the data that is currently available in industry and use the predictions to generate tailored near-optimal meshes for each case. With this strategy the mesh generation stage is no longer time consuming and does not require the input of an expert engineer. In the current example, each near-optimal mesh is generated in 10 min using a single processor. The near-optimal meshes have between 5 M and 6.5 M elements for all the cases considered, which is a fraction of the number of elements required for the fixed-mesh approach currently employed in practice. For the near-optimal meshes, the CFD simulations run on 24 processors, with 96GB available memory, and the solution requires between 40 min and one hour and 20 min. It is worth noting that the variation of the time required for the solution is induced by the variation in the mesh that is required for each case.

Table 7 summarises the carbon footprint and energy consumption induced by the proposed approach. This includes the resources required to tune the hyperparameters of the network, the generation of 143 near-optimal meshes and the associated CFD simulations. It is worth noting that the time required for tuning accounts for the fact that the experiments to tune the NNs were repeated five times, to minimise the effect of the random initialisation of the NN weights.

Table 7 Carbon footprint and energy consumption for the parametric study using the proposed approach to train a NN, including tuning the hyperparameters, predict the near-optimal meshes and run the CFD simulations

The footprint of the proposed approach is dominated by the tuning of the NN, which is a figure that is not reported on many occasions [10]. Despite a grid search was used to find the best hyperparameters and experiments were repeated five times, the total carbon footprint and energy consumption is more than 35 times lower than using the common practice of running all cases on a single mesh.

It is worth noting that it is possible to reduce the computational cost of performing the simulations in a very fine mesh by utilising the solution with a certain Mach number and/or angle of attack for another case. However, it is very important to note that the proposed approach also permits this type of solution restarting after interpolating one computed solution to a new predicted mesh. Therefore, the gain is expected to be very similar to the one reported here. In addition, it is worth mentioning that on some occasions this restarting approach is not preferred because it requires running all the cases serially.

6 Concluding remarks

A novel method to predict the characteristics of sources that are used to control the spacing in an unstructured mesh generation algorithm has been proposed. The method provides the ability to automatically predict the near-optimal mesh for an unseen flow condition or geometric configuration, using historic data accumulated from previous CFD analysis.

It is assumed that a database of accurate solutions is available for a variety of flow conditions and/or geometric configurations. The strategy involves four steps. First, for every solution available, a set of mesh sources is created. Each source has five characteristics, namely the three spatial coordinates, the spacing required at the vicinity of the point and the radius of influence. A procedure to create the sources that will enable reproducing the spacing function that will produce a mesh capable of accurately reproducing the given solution is proposed. The second step involves combining the sources of multiple cases into a single set of global mesh sources. A process to combine the sources into a global set is proposed. The resulting set of global sources will enable the generation of meshes that are suitable to capture all the solutions of a given set of cases. The third step involves the use of machine learning. A NN is trained to predict the characteristics of the global set of sources. Once trained, the NN is used to predict the characteristics of the mesh sources for unseen flow conditions and/or geometric configurations. The last step, aimed at improving the efficiency of the mesh generation process, removes surplus sources and merge point sources into line sources when possible.

The ability of the proposed strategy to predict the near-optimal mesh for unseen flow conditions and/or geometric configurations is tested using three numerical examples. The examples utilise a database of three dimensional inviscid compressible flow solutions for varying inflow conditions and geometric parameters. Numerical experiments are reported to show the influence of the NN architecture and the size of the training dataset in the prediction capability of the NN. Even with a reduced training dataset, the mesh characteristics are accurately predicted. Furthermore, the near-optimal meshes constructed with the predicted characteristics of the sources are used to compute CFD solutions. The results show that even in the most complicated example, with eight parameters of different nature (i.e. flow conditions and geometric parameters), the resulting meshes lead to accurate CFD solutions. More precisely, the computed aerodynamic quantities using the near-optimal meshes are within the required accuracy for the aerospace industry, i.e. less than five lift/drag counts difference with respect to the target solution.

To conclude, the proposed approach was analysed in terms of efficiency and the environmental implications were discussed. The analysis showed that the technique proposed in this work is capable of reducing the carbon footprint of computations by a factor of 35, when compared to the current practice in industry. This factor was obtained by accounting for the whole cost of the proposed technique, that is including the resources required to train multiple NN and fine tune the hyperparameters.

Total least-squares approximations in three dimensions

Finding the plane or line that produces the best fit to a given set of points is a classical problem in many applications of science and engineering. To define what is considered the best fit, it is necessary to specify a measure for the deviation of a point with respect to a plane or line. On many occasions, a simple measure that involves one of the coordinates is considered, but the result is highly dependent on the particular arrangement of the given set of points. This section describes the procedure to fit a plane or a line to a set of points in three dimensions by employing the true distance, measured in the orthogonal direction. This is a particular case of the technique usually referred to as the total least-squares.[9]

1.1 Fitting a plane to a set of points using orthogonal regression

Let us consider a set of n points in $\mathbb {R}^3$, denoted by $\mathcal {X} = \{ {\varvec{x}}_i\}_{i=1,\ldots ,n}$, and a plane, $\mathcal {P}$, defined by a point ${\varvec{x}}_0 \in \mathbb {R}^3$ and a unit normal vector ${\varvec{n}}$. By definition, a point ${\varvec{x}}\in \mathcal {P}$ satisfies ${\varvec{n}}\cdot ({\varvec{x}}-{\varvec{x}}_0)=0$. A generic point ${\varvec{x}}_i \in \mathcal {X}$ can be expressed as

$$\begin{aligned} {\varvec{x}}_i = {\varvec{x}}_0 + \lambda _i {\varvec{n}}+ \zeta _i {\varvec{t}}, \end{aligned}$$

(13)

where $\lambda _i = {\varvec{n}}\cdot ({\varvec{x}}_i-{\varvec{x}}_0)$ is the distance from the point ${\varvec{x}}_i$ to the plane $\mathcal {P}$, $\zeta _i$ is the distance from the orthogonal projection of ${\varvec{x}}_i$ onto $\mathcal {P}$, namely ${\varvec{\hat{x}}}_i$, to the point ${\varvec{x}}_0$ and ${\varvec{t}}= ({\varvec{\hat{x}}}_i - {\varvec{x}}_0)/\Vert {\varvec{\hat{x}}}_i - {\varvec{x}}_0)\Vert$.

To find the plane that best fits the given set of points, the point ${\varvec{x}}_0$ and the unit normal vector ${\varvec{n}}$ that minimises the energy function given by

$$\begin{aligned} E({\varvec{x}}_0,{\varvec{n}})= \sum ^{n}_{i=1} \lambda ^2_i={\varvec{n}}^T{\varvec{M}}{\varvec{n}}\end{aligned}$$

(14)

are sought, where ${\varvec{M}}:= \displaystyle \sum ^{n}_{i=1} \left( {\varvec{x}}_i-{\varvec{x}}_0 \right) \left( {\varvec{x}}_i-{\varvec{x}}_0 \right) ^T$.

To simplify the minimisation problem, the point ${\varvec{x}}_0$ is taken as the average position of the given set of points $\mathcal {X}$, namely ${\varvec{x}}_0 = \displaystyle \sum ^{n}_{i=1} {\varvec{x}}_i/n$. With this choice, the energy function becomes a quadratic form and the unit normal vector ${\varvec{n}}$ that provides the minimum of $E({\varvec{n}})$ is simply the normalised eigenvector corresponding to the minimum eigenvalue of the matrix ${\varvec{M}}$.

1.2 Fitting a line to a set of points using orthogonal regression

Let us consider a set of n points in $\mathbb {R}^3$, denoted by $\mathcal {X} = \{ {\varvec{x}}_i\}_{i=1,\ldots ,n}$, and a line, $\ell$, defined by a point ${\varvec{x}}_0 \in \mathbb {R}^3$ and a unit vector ${\varvec{t}}$. By definition, a point ${\varvec{x}}\in \ell$ satisfies ${\varvec{t}}\times ({\varvec{x}}-{\varvec{x}}_0) = {\varvec{0}}$. A generic point ${\varvec{x}}_i \in \mathcal {X}$ can be expressed as

$$\begin{aligned} {\varvec{x}}_i = {\varvec{x}}_0 + \lambda _i {\varvec{n}}+ \zeta _i {\varvec{t}}, \end{aligned}$$

(15)

where $\lambda _i = {\varvec{t}}\cdot ({\varvec{x}}_i-{\varvec{x}}_0)$ is the distance from ${\varvec{x}}_0$ to the orthogonal projection of ${\varvec{x}}_i$ onto the line $\ell$, namely ${\varvec{\hat{x}}}_i$. The coefficient $\zeta _i = \Vert {\varvec{x}}_i - {\varvec{\hat{x}}}_i\Vert =\Vert {\varvec{x}}_i - {\varvec{x}}_0 - \lambda _i {\varvec{t}}\Vert$ represents the distance from ${\varvec{x}}_i$ to its orthogonal projection onto the line $\ell$.

To find the line that best fits the given set of points, the point ${\varvec{x}}_0$ and the unit vector ${\varvec{t}}$ that minimises the energy function given by

$$\begin{aligned} E({\varvec{x}}_0,{\varvec{t}})= \sum ^{n}_{i=1} \zeta ^2_i={\varvec{t}}^T{\varvec{\widehat{M}}}{\varvec{t}}\end{aligned}$$

(16)

are sought, where ${\varvec{\widehat{M}}}= {{\,\mathrm{tr}\,}}({\varvec{M}}){\varvec{I}} - {\varvec{M}}$ and ${\varvec{M}}:= \displaystyle \sum ^{n}_{i=1} \left( {\varvec{x}}_i-{\varvec{x}}_0 \right) \left( {\varvec{x}}_i-{\varvec{x}}_0 \right) ^T$.

To simplify the minimisation problem, the point ${\varvec{x}}_0$ is taken as the average position of the given set of points $\mathcal {X}$, namely ${\varvec{x}}_0 = \displaystyle \sum ^{n}_{i=1} {\varvec{x}}_i/n$. With this choice, the energy function becomes a quadratic form and the unit vector ${\varvec{t}}$ that provides the minimum of $E({\varvec{t}})$ is the normalised eigenvector corresponding to the minimum eigenvalue of the matrix ${\varvec{\widehat{M}}}$.