Skip to main content
SpringerLink
Log in

Comparative study of modelling flows in porous media for engineering applications using finite volume and artificial neural network methods

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

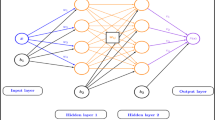
A neural solution methodology, using a feed-forward and a convolutional neural networks, is presented for general tensor elliptic pressure equation with discontinuous coefficients. The methodology is applicable for solving single-phase flow in porous medium, which is traditionally solved using numerical schemes like finite-volume methods. The neural solution to elliptic pressure equation is based on machine learning algorithms and could serve as a more effective alternative to finite volume schemes like two-point or multi-point discretization schemes (TPFA or MPFA) for faster and more accurate solution of elliptic pressure equation. Series of 1D and 2D test cases, where the results of Neural solutions are compared to numerical solutions obtained using two-point schemes with range of heterogeneities, are also presented to demonstrate general applicability and accuracy of the Neural solution method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23

Similar content being viewed by others

Notes

  1. A grid is called orthogonal if all grid lines intersect at a right angle.

References

  1. Durlofsky LJ (1993) A triangle based mixed finite element finite volume technique for modeling two phase flow through porous media. J Comput Phys 1:252–266

    Article  Google Scholar 

  2. Edwards MG (2002) Unstructured, control-volume distributed, full-tensor finite volume schemes with flow based grids. Comput Geo 6:433–452

    Article  MathSciNet  Google Scholar 

  3. Eigestad GT, Klausen RA (2005) On convergence of multi-point flux approximation o-method; numerical experiment for discontinuous permeability. (2nd edn). Submitted to Numer Meth Part Diff Eqs

  4. Guo X, Li W, Iorio F (2016) Convolutional neural networks for steady flow approximation. https://doi.org/10.1145/2939672.2939738

  5. Hagan MT, Demuth HB, Beale MH (1996) Neural Network Design. PWS Publishing, Boston

    Google Scholar 

  6. Li Z, Kovachki N, Azizzadenesheli K, Liu B, Bhattacharya K, Stuart A, Anandkumar A (2021) Fourier neural operator for parametric partial differential equations. https://doi.org/10.48550/arXiv.2010.08895.

  7. Pal M, Makauskas P, Malik S (2023) Upscaling porous media using neural networks: a deep learning approach to homogenization and averaging. https://doi.org/10.3390/pr11020601

  8. Recktenwald G (2014) The control-volume finite-difference approximation to the diffusion equation

  9. Aavatsmark I (2002) Introduction to multipoint flux approximation for quadrilateral grids. Comput Geo No 6:405–432

    Article  MathSciNet  Google Scholar 

  10. Kirill Zubov et al. (2021) NeuralPDE: automating physics-informed neural networks (PINNs) with error approximations. http://arxiv.org/2107.09443arXiv:https://arxiv.org/abs/2107.09443

  11. The Julia Programming Language. Version 1.7.3 (2022) Jeff Bezanson, Alan Edelman, Viral B. Shah and Stefan Karpinski, 2009, https://julialang.org/

  12. Pal M, Edwards MG (2006) Effective upscaling using a family of flux-continuous, finite-volume schemes for the pressure equation. In Proceedings, ACME 06 Conference, Queens University Belfast, Northern Ireland-UK, pages 127–130

  13. Pal M, Edwards MG, Lamb AR (2006) Convergence study of a family of flux-continuous, Finite-volume schemes for the general tensor pressure equation. Numer Method Fluids 51(9–10):1177–1203

    Article  MathSciNet  Google Scholar 

  14. Pal M (2007) Families of control-volume distributed cvd(mpfa) finite volume schemes for the porous medium pressure equation on structured and unstructured grids. PhD Thesis, University of Wales, Swansea-UK

  15. Pal M, Edwards MG (2008) The competing effects of discretization and upscaling - A study using the q-family of CVD-MPFA. ECMOR 2008 - 11th European Conference on the Mathematics of Oil Recovery

  16. Pal M (2010) The effects of control-volume distributed multi-point flux approximation (CVD-MPFA) on upscaling-A study using the CVD-MPFA schemes. Int J Numer Methods Fluids 68:1

    MathSciNet  Google Scholar 

  17. Pal M, Edwards MG (2011) Non-linear flux-splitting schemes with imposed discrete maximum principle for elliptic equations with highly anisotropic coefficients. Int J Numer Method Fluids 66(3):299–323

    Article  MathSciNet  Google Scholar 

  18. Pal M (2012) A unified approach to simulation and upscaling of single-phase flow through vuggy carbonates. Intl J Numer Method Fluids. https://doi.org/10.1002/fld.2630

    Article  Google Scholar 

  19. Pal M, Edwards MG (2012) The effects of control-volume distributed multi-point flux approximation (CVD-MPFA) on upscaling-A study using the CVD-MPFA schemes. Int J Numer Methods Fluids. https://doi.org/10.1002/fld.2492

    Article  MathSciNet  Google Scholar 

  20. Zhang Wenjuan, Kobaisi Al, Mohammed, (2022) On the monotonicity and positivity of physics-informed neural networks for highly anisotropic diffusion equations. MDPI Energ 15:6823

  21. Ahmad S Abushaika (2013) Numerical methods for modelling fluid flow in highly heterogeneous and fractured reservoirs

  22. Pal M, Lamine S, Lie K-A, Krogstad S (2015) Validation of multiscale mixed finite-element method. Int J Numer Methods Fluids 77:223

    Article  MathSciNet  Google Scholar 

  23. Pal M (2021) On application of machine learning method for history matching and forecasting of times series data from hydrocarbon recovery process using water flooding. Petrol Sci Technol 39:15–16

    Article  Google Scholar 

  24. Pal M, Makauskas P, Saxena P, Patil P (2022) The neural upscaling method for single-phase flow in porous medium. Paper Presented at EAGE-ECMOR 2022 Conference

  25. Ken Perlin (1985) An image synthesizer. SIGGRAPH. Comput Graph 19:287–296. https://doi.org/10.1145/325165.32524

    Article  Google Scholar 

  26. Ricky TQ, Chen Yulia Rubanova, Jesse Bettencourt, David Duvenaud (2018) Neural ordinary differential equations. 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Canada

  27. Vasilyeva M, Tyrylgin A (2018) Machine learning for accelerating effective property prediction for poroelasticity problem in stochastic media. arXiv:https://arxiv.org/abs/1810.01586

  28. Wu J-L, XioaH Paterson EG (2018) Physics-informed machine learning approach for augmenting turbulence models: A comprehensive framework. Phys Rev Fluids 2:073602

    Google Scholar 

  29. Russel TF, Wheeler MF (1983) Finite element and finite difference methods for continuous flows in porous media. Chapter 2, in the Mathematics of Reservoir Simulation, R.E. Ewing ed. Front Appl Math SIAM pp 35–106

  30. Raissi M, Perdikaris P, Karniadakis GE (2019) Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys 378:686–707

    Article  MathSciNet  Google Scholar 

  31. Zhao J, Zhao W, Ma Z, Yong WA, Dong B (2022) Finding models of heat conduction via machine learning. Int J Heat Mass Transfer 185:122396

    Article  Google Scholar 

  32. Huang S, Tao B, Li J, Yin Z (2019) On-line heat flux estimation of a nonlinear heat conduction system with complex geometry using a sequential inverse method and artificial neural network. Int J Heat Mass Transfer 143:118491

    Article  Google Scholar 

  33. Wang Y, Zhang S, Ma Z, Yang Q (2020) Artificial neural network model development for prediction of nonlinear flow in porous media. Powder Technol 373:274–288

    Article  Google Scholar 

  34. Abad JMN, Alizadeh R, Fattahi A, Doranehgard MH, Alhajri E, Karimi N (2020) Analysis of transport processes in a reacting flow of hybrid nanofluid around a bluff-body embedded in porous media using artificial neural network and particle swarm optimization. J Mol Liquids 313:113492

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematical Modelling, KTU, Studentu 50-239, Kanuas, LT-51368, Kanuas, Lithuania

    Pijus Makauskas & Mayur Pal

  2. Department of Mechanical Engineering, IIT Ropar, Satish Dhawan Block, Rupnagar, 140001, Punjab, India

    Vismay Kulkarni, Abhishek Singh Kashyap & Himanshu Tyagi

Authors
  1. Pijus Makauskas
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mayur Pal
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Vismay Kulkarni
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Abhishek Singh Kashyap
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Himanshu Tyagi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mayur Pal.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Makauskas, P., Pal, M., Kulkarni, V. et al. Comparative study of modelling flows in porous media for engineering applications using finite volume and artificial neural network methods. Engineering with Computers 39, 3773–3789 (2023). https://doi.org/10.1007/s00366-023-01814-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-023-01814-x

Keywords

Search

Navigation