A time-marching procedure based on a sub-step explicit time integration scheme for non-viscous damping systems

Abstract

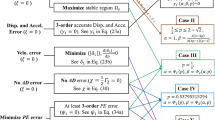
An improved time-marching procedure based on a composite explicit method is proposed for non-viscous damping systems. In this method, an improved integral approximation scheme is developed to improve the convolution solution accuracy and is applicable to any causal kernel function. The mathematical derivation and calculation procedure based on the composite explicit method are formulated for non-viscous damping systems. The adopted composite explicit method shows more desirable stability and accuracy properties than other competitive explicit methods. Numerical simulations of some representative examples demonstrate the proposed time-marching procedure is efficient for the dynamic analysis of non-viscous damping systems.

Appendices

Appendix A: The Noh-Bathe method for non-viscous damping systems

Here the calculation procedure of the Noh-Bathe method for non-viscous systems is provided. The Noh-Bathe method is a classical explicit time integration method that divides each time step $\Delta t$ into two sub-steps. The time step sizes are $p\Delta t$ for the first sub-step and $\left(1-p\right)\Delta t$ for the second sub-step, where $0<p<1$. The improved integral approximation scheme to deal with the convolution of damping force is adopted here.

The governing equation for non-viscous damping systems at time $t+p\Delta t$ and $t+\Delta t$ can be found in Eqs. (4) and (21), respectively. The initial displacement and velocity can be obtained by Eq. (3). For the first sub-step, the non-viscous damping force is written as

$${{{\varvec{F}}}_{\mathrm{damp}}^{^{\prime}}={\varvec{F}}}_{\mathrm{damp}1}^{^{\prime}}+{{\varvec{F}}}_{\mathrm{damp}2}^{^{\prime}}={\varvec{C}}{\int }_{0}^{{t}_{i+p}}g\left({t}_{i+p}-\tau \right)\bullet \dot{{\varvec{x}}}\left(\tau \right)\mathrm{d}\tau$$

(62)

where

$${{\varvec{F}}}_{\mathrm{damp}1}^{^{\prime}}={\varvec{C}}\sum_{j=0}^{i-1}{\int }_{{t}_{j}}^{{t}_{j+1}}g\left({t}_{i+p}-\tau \right)\bullet \dot{{\varvec{x}}}\left(\tau \right)\mathrm{d}\tau$$

(63)

$${{\varvec{F}}}_{\mathrm{damp}2}^{^{\prime}}={\varvec{C}}{\int }_{{t}_{i}}^{{t}_{i+p}}g\left({t}_{i+p}-\tau \right)\bullet \dot{{\varvec{x}}}\left(\tau \right)\mathrm{d}\tau$$

(64)

The velocity function vector $\dot{{\varvec{x}}}\left(\tau \right)$ of ${{\varvec{F}}}_{\mathrm{damp}1}^{^{\prime}}$ and ${{\varvec{F}}}_{\mathrm{damp}2}^{^{\prime}}$ can be, respectively, expressed as

$$\dot{{\varvec{x}}}\left(\tau \right)=\dot{{\varvec{x}}}\left({t}_{j}\right)+\frac{\tau -{t}_{j}}{2}\left(\ddot{{\varvec{x}}}\left({t}_{j}\right)+\ddot{{\varvec{x}}}\left({t}_{j+1}\right)\right)$$

(65)

$$\dot{{\varvec{x}}}\left(\tau \right)=\dot{{\varvec{x}}}\left({t}_{i}\right)+(\tau -{t}_{i})\ddot{{\varvec{x}}}\left({t}_{i}\right)$$

(66)

Substituting (65) and (66) into (63) and (64) respectively, the damping force for the first sub-step is rewritten as

$${{\varvec{F}}}_{\mathrm{damp}1}^{^{\prime}}={\varvec{C}}{\sum }_{j=0}^{i-1}{\int }_{{t}_{j}}^{{t}_{j+1}}g\left({t}_{i+p}-\tau \right)\bullet \left(\dot{{\varvec{x}}}\left({t}_{j}\right)+\frac{\tau -{t}_{j}}{2}\left(\ddot{{\varvec{x}}}\left({t}_{j}\right)+\ddot{{\varvec{x}}}\left({t}_{j+1}\right)\right)\right)\mathrm{d}\tau$$

(67)

$${{\varvec{F}}}_{\mathrm{damp}2}^{^{\prime}}={\varvec{C}}{\int }_{{t}_{i}}^{{t}_{i+p}}g\left({t}_{i+p}-\tau \right)\bullet \left(\dot{{\varvec{x}}}\left({t}_{i}\right)+(\tau -{t}_{i})\ddot{{\varvec{x}}}\left({t}_{i}\right)\right)\mathrm{d}\tau$$

(68)

For nonintegrable functions, the damping force can be formulated as follow

$${{\varvec{F}}}_{\mathrm{damp}1}^{^{\prime}}={\varvec{C}}{\sum }_{j=0}^{i-1}{\int }_{{t}_{j}}^{{t}_{j+1}}{\sum }_{k=0}^{N}\frac{{g}^{\left(k\right)}\left({t}_{i+p}-{t}_{j}\right)}{k!}\left({\left({t}_{j}-\tau \right)}^{k}\bullet \dot{{\varvec{x}}}\left({t}_{j}\right)-{\left({t}_{j}-\tau \right)}^{k+1}\bullet \frac{\ddot{{\varvec{x}}}\left({t}_{j}\right)+\ddot{{\varvec{x}}}\left({t}_{j+1}\right)}{2}\right)\mathrm{d}\tau$$

(69)

$${{\varvec{F}}}_{\mathrm{damp}2}^{^{\prime}}={\varvec{C}}{\int }_{{t}_{i}}^{{t}_{i+p}}{\sum }_{k=0}^{N}\frac{{g}^{\left(k\right)}\left(p\Delta t\right)}{k!}\left({\left({t}_{j}-\tau \right)}^{k}\bullet \dot{{\varvec{x}}}\left({t}_{j}\right)-{\left({t}_{j}-\tau \right)}^{k+1} \ddot{{\varvec{x}}}\left({t}_{j}\right)\right)\mathrm{d}\tau$$

(70)

The acceleration vector for the first sub-step is obtained as

$${\varvec{M}}\ddot{{\varvec{x}}}\left({t}_{i+p}\right)={\varvec{F}}\left({t}_{i+p}\right)-{{\varvec{F}}}_{\mathrm{damp}}^{^{\prime}}-{\varvec{K}}{\varvec{x}}\left({t}_{i+p}\right)$$

(71)

The displacement vector for the first sub-step can be calculated by

$${\varvec{x}}({t}_{i+p})={\varvec{x}}\left({t}_{i}\right)+p\Delta t\bullet \dot{{\varvec{x}}}\left({t}_{i}\right)+\frac{1}{2}{\left(p\Delta t\right)}^{2}\bullet \ddot{{\varvec{x}}}\left({t}_{i}\right)$$

(72)

The velocity vector for the first sub-step is adopted as

$$\dot{{\varvec{x}}}\boldsymbol{ }({t}_{i+p})=\dot{{\varvec{x}}}\boldsymbol{ }({t}_{i})+\frac{p\Delta t}{2}\bullet \left(\ddot{{\varvec{x}}}\left({t}_{i}\right)+ \ddot{{\varvec{x}}}\left({t}_{i+p}\right)\right)$$

(73)

For the second sub-step, the non-viscous damping force can be written as

$${{\varvec{F}}}_{\mathrm{damp}}={{\varvec{F}}}_{\mathrm{damp}1}+{{\varvec{F}}}_{\mathrm{damp}2}={\varvec{C}}{\int }_{0}^{{t}_{i+1}}g\left({t}_{i+1}-\tau \right)\bullet \dot{{\varvec{x}}}\left(\tau \right)\mathrm{d}\tau$$

(74)

where

$${{\varvec{F}}}_{\mathrm{damp}1}={\varvec{C}}\sum_{j=0}^{i-1}{\int }_{{t}_{j}}^{{t}_{j+1}}g\left({t}_{i+1}-\tau \right)\bullet \dot{{\varvec{x}}}\left(\tau \right)\mathrm{d}\tau$$

(75)

$${{\varvec{F}}}_{\mathrm{damp}2}={\varvec{C}}{\int }_{{t}_{i}}^{{t}_{i+1}}g\left({t}_{i+1}-\tau \right)\bullet \dot{{\varvec{x}}}\left(\tau \right)\mathrm{d}\tau$$

(76)

The velocity vector functions $\dot{{\varvec{x}}}\left(\tau \right)$ can be, respectively, substituted as the Eqs. (65) and (66). Then, the ${{\varvec{F}}}_{\mathrm{damp}1}$ and ${{\varvec{F}}}_{\mathrm{damp}2}$ can be rewritten as

$${{\varvec{F}}}_{\mathrm{damp}1}={\varvec{C}}\sum_{j=0}^{i-1}{\int }_{{t}_{j}}^{{t}_{j+1}}g\left({t}_{i+1}-\tau \right)\bullet \left(\dot{{\varvec{x}}}\left({t}_{j}\right)+\frac{\tau -{t}_{j}}{2}\left(\ddot{{\varvec{x}}}\left({t}_{j}\right)+\ddot{{\varvec{x}}}\left({t}_{j+1}\right)\right)\right)\mathrm{d}\tau$$

(77)

$${{\varvec{F}}}_{\mathrm{damp}2}={\varvec{C}}{\int }_{{t}_{i}}^{{t}_{i+1}}g\left({t}_{i+1}-\tau \right)\bullet \left(\dot{{\varvec{x}}}\left({t}_{i}\right)+(\tau -{t}_{i})\ddot{{\varvec{x}}}\left({t}_{i}\right)\right)\mathrm{d}\tau$$

(78)

If closed-form solutions of the above integrals cannot be obtained directly, the damping force for the second sub-step can be formulated as follow

$${{\varvec{F}}}_{\mathrm{damp}1}={\varvec{C}}{\sum }_{j=1}^{i-1}{\int }_{{t}_{j}}^{{t}_{j+1}}{\sum }_{k=0}^{N}\frac{{g}^{\left(k\right)}\left({t}_{i+1}-{t}_{j}\right)}{k!}\left({\left({t}_{j}-\tau \right)}^{k}\bullet \dot{{\varvec{x}}}\left({t}_{j}\right)-{\left({t}_{j}-\tau \right)}^{k+1}\bullet \frac{\ddot{{\varvec{x}}}\left({t}_{j}\right)+\ddot{{\varvec{x}}}\left({t}_{j+1}\right)}{2}\right)\mathrm{d}\tau$$

(79)

$${{\varvec{F}}}_{\mathrm{damp}2}={\varvec{C}}{\int }_{{t}_{i}}^{{t}_{i+1}}{\sum }_{k=0}^{N}\frac{{g}^{\left(k\right)}\left(\Delta t\right)}{k!}\left({\left({t}_{i}-\tau \right)}^{k}\bullet \dot{{\varvec{x}}}\left({t}_{i}\right)-{\left({t}_{i}-\tau \right)}^{k+1} \ddot{{\varvec{x}}}\left({t}_{i}\right)\right)\mathrm{d}\tau$$

(80)

The final acceleration vector for the second sub-step is solved by

$${\varvec{M}}\ddot{{\varvec{x}}}\left({t}_{i+1}\right)={\varvec{F}}\left({t}_{i+1}\right)-{{\varvec{F}}}_{\mathrm{damp}}-{\varvec{K}}{\varvec{x}}\left({t}_{i+1}\right)$$

(81)

The final displacement vector for the second sub-step is formulated as

$${\varvec{x}}({t}_{i+1})={\varvec{x}}\left({t}_{i+p}\right)+(1-p)\Delta t\bullet \dot{{\varvec{x}}}\left({t}_{i+p}\right)+\frac{1}{2}{\left((1-p)\Delta t\right)}^{2}\bullet \ddot{{\varvec{x}}}\left({t}_{i+p}\right)$$

(82)

The final velocity vector for the second sub-step is calculated by

$$\dot{{\varvec{x}}}\left({t}_{i+1}\right)=\dot{{\varvec{x}}}\left({t}_{i+p}\right)+\frac{p\Delta t}{2}\bullet \left(\frac{-2{p}^{2}+3p-1}{2p}\Delta t\bullet \ddot{{\varvec{x}}}\left({t}_{i}\right)+ \frac{-{p}^{2}-p+1}{2p}\Delta t\bullet \ddot{{\varvec{x}}}\left({t}_{i+p}\right)+\frac{p}{2}\Delta t\bullet \ddot{{\varvec{x}}}\left({t}_{i+p}\right)\right)$$

(83)

Appendix B: The theoretical solution of the system in numerical example 1

The dynamic kernel governing equation of the SDOF system under sinusoidal load is express as

$$m\ddot{x}\left(t\right)+c{\int }_{0}^{t}\mu {e}^{-\mu (t-\tau )}\bullet \dot{x}\left(\tau \right)\mathrm{d}\tau +kx\left(t\right)={f}_{0}\mathrm{sin}(\theta t)$$

(84)

with initial conditions $x\left(0\right)={x}_{0}$, $\dot{x}\left(0\right)={v}_{0}$, and the initial acceleration value can be calculated as $\ddot{x}\left(0\right)=-\frac{kx\left(0\right)}{m}$.

After Laplace transformation, Eq. (84) can be rewritten as

$$\left[m{s}^{2}+s\frac{c\mu }{s+\mu }+k\right]\bullet X(s)=\frac{{f}_{0}\theta }{{s}^{2}+{\theta }^{2}}$$

(85)

where $s$ is the Laplace domain parameter.

The Eq. (87) can be rewritten as

$$\left[{s}^{3}+\mu {s}^{2}+\left(\frac{c\mu }{m}+\frac{k}{m}\right)s+\frac{k\mu }{m}\right]\bullet X(s)=\frac{{f}_{0}\theta (s+\mu )}{m\left({s}^{2}+{\theta }^{2}\right)}$$

(86)

The characteristic equation is expressed as

$${s}^{3}+\mu {s}^{2}+\left(\frac{c\mu }{m}+\frac{k}{m}\right)s+\frac{k\mu }{m}=0$$

(87)

Let $a$,$b$,$c$,$d$ represent coefficients of the cubic term, the quadratic term, the first-order term and the zeroth-order term of the above equation, respectively. That is, $a=1$,$b=\mu$,$c=\frac{c\mu }{m}+\frac{k}{m}$,$d=\frac{k\mu }{m}$.

The roots of Eq. (88) are given as

$${s}_{1}=-\frac{b}{3a}+u+\nu$$

(88)

$${s}_{2}=-\frac{b}{3a}+\frac{-1+\sqrt{3}i}{2}u+{\left(\frac{-1+\sqrt{3}i}{2}\right)}^{2}\nu =-\frac{b}{3a}-\frac{1}{2}\left(u+\nu \right)-\frac{\sqrt{3}}{2}\left(u-\nu \right)i$$

(89)

$${s}_{3}=-\frac{b}{3a}+{\left(\frac{-1+\sqrt{3}i}{2}\right)}^{2}u+\frac{-1+\sqrt{3}i}{2}\nu =-\frac{b}{3a}-\frac{1}{2}\left(u+\nu \right)+\frac{\sqrt{3}}{2}\left(u-\nu \right)i$$

(90)

where $u=\sqrt[3]{{\eta }^{2}+\sqrt{{\eta }^{2}+{\zeta }^{3}}}$, $\nu =\sqrt[3]{{\eta }^{2}-\sqrt{{\eta }^{2}+{\zeta }^{3}}}$, $\eta =\frac{9abc-27{a}^{2}d-2{b}^{3}}{54{a}^{3}}$, $\zeta =\frac{3ac-{b}^{2}}{9{a}^{2}}$. And let $\alpha$ and $\beta$ be the real and imaginary parts of ${s}_{3}$, respectively. That is, $\alpha =-\frac{b}{3a}-\frac{1}{2}\left(u+\nu \right)$, $\beta =\frac{\sqrt{3}}{2}\left(u-\nu \right)$.

Then, the general solution of a homogeneous equation in the time domain can be adopted as

$${x}_{1}\left(t\right)={A}_{1}{e}^{{s}_{1}t}+{e}^{\alpha t}\left({A}_{2}cos\left(\beta t\right)+{A}_{3}\mathrm{sin}\left(\beta t\right)\right)$$

(91)

where

$${A}_{1}=\frac{\ddot{x}\left(0\right)-2\alpha \dot{x}\left(0\right)+x\left(0\right)\bullet \left({\alpha }^{2}+{\beta }^{2}\right)}{{\alpha }^{2}-2\alpha {s}_{1}+{\beta }^{2}+{s}_{1}^{2}}$$

(92a)

$${A}_{2}=\frac{-\ddot{x}\left(0\right)+2\alpha \dot{x}\left(0\right)-x\left(0\right)\bullet \left(2\alpha {s}_{1}-{s}_{1}^{2}\right)}{{\alpha }^{2}-2\alpha {s}_{1}+{\beta }^{2}+{s}_{1}^{2}}$$

(92b)

$${A}_{3}=\frac{\ddot{x}\left(0\right)\left(\alpha -{s}_{1}\right)+\dot{x}\left(0\right)\left({-\alpha }^{2}+{\beta }^{2}+{s}_{1}^{2}\right)-x\left(0\right)\bullet \left({-\alpha }^{2}{s}_{1}+{\beta }^{2}{s}_{1}+\alpha {s}_{1}^{2}\right)}{{\alpha }^{2}\beta -2\alpha \beta {s}_{1}+{\beta }^{3}+\beta {s}_{1}^{2}}$$

(92c)

Adopting inverse Laplace transform, Eq. (86) can transform into the time domain as

$$\dddot x\left( t \right) + \mu \ddot{x}\left( t \right) + \left( {\frac{c\mu }{m} + \frac{k}{m}} \right)\dot{x}\left( t \right) + \frac{k\mu }{m}x\left( t \right) = \frac{{f_{0} \theta }}{m}{\text{sin}}\left( {\theta t} \right) + \frac{{f_{0} \mu }}{m}{\text{cos}}\left( {\theta t} \right)$$

(93)

The special solution form of the nonhomogeneous differential Eq. (93) can be assumed to be

$${x}_{2}\left(t\right)=A\mathrm{sin}\left(\theta t\right)+B\mathrm{cos}\left(\theta t\right)$$

(94)

Substituting Eq. (94) into Eq. (93), the values of $A$ and $B$ can be obtained as

$$A=\frac{\frac{{f}_{0}\theta }{m}e-\frac{{f}_{0}\mu }{m}f}{{e}^{2}+{f}^{2}}$$

(95a)

$$B=\frac{\frac{{f}_{0}\theta }{m}e+\frac{{f}_{0}\mu }{m}f}{{e}^{2}+{f}^{2}}$$

(95b)

where $e=\frac{k\mu }{m}-\mu {\theta }^{2}$, $f={\theta }^{3}-\frac{\theta \left(c\mu +k\right)}{m}$.

The general solution of Eq. (84) can be written as

$$x\left(t\right)={{x}_{1}\left(t\right)+x}_{2}\left(t\right)$$

(96)