Skip to main content

Advertisement

Springer Nature Link
Log in

An SPH-based FSI framework for phase-field modeling of brittle fracture under extreme hydrodynamic events

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

We present a proof-of-concept particle-based fluid–structure interaction (FSI) computational framework for modeling structural fracture and fragmentation under the impact of extreme hydrodynamic events. The smoothed particle hydrodynamics (SPH) approach is employed to discretize the equations of motion for both the fluid and structural domains. The meshfree nature of the discretization technique accommodates the simulation of scenarios involving extreme structural deformations and material separation, as well as free-surface flows. The framework is supplemented with a phase-field model of brittle fracture that allows for the simulation of crack nucleation, propagation, and branching, which leads to realistic modeling of structural responses during extreme hydrodynamic events. In the end, a novel algorithm for coupling the fluid and solid subproblems is presented. The proposed approach is verified and validated against existing computational methods and experimental results, and in the end, a few challenging problems involving complex fracture patterns and fragmentation are presented.

Graphical abstract

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30
Fig. 31
Fig. 32
Fig. 33
Fig. 34
Fig. 35
Fig. 36
Fig. 37
Fig. 38
Fig. 39
Fig. 40

Similar content being viewed by others

References

  1. Najibi N, Devineni N (2018) Recent trends in the frequency and duration of global floods. Earth Syst Dyn 9(2):757–783

    Google Scholar 

  2. NOAA NCEI (2022) Noaa national centers for environmental information (NCEI) U.S. billion-dollar weather and climate disasters

  3. Monaghan JJ (1994) Simulating free surface flows with SPH. J Comput Phys 110(2):399–406

    MATH  Google Scholar 

  4. Chen LF, Zang J, Hillis AJ, Morgan GCJ, Plummer AR (2014) Numerical investigation of wave-structure interaction using OpenFoam. Ocean Eng 88:91–109

    Google Scholar 

  5. Wei Z, Dalrymple RA, Hérault A, Bilotta G, Rustico E, Yeh H (2015) SPH modeling of dynamic impact of tsunami bore on bridge piers. Coast Eng 104:26–42

    Google Scholar 

  6. Akbari H (2017) Simulation of wave overtopping using an improved SPH method. Coast Eng 126:51–68

    Google Scholar 

  7. Sarfaraz M, Pak A (2017) SPH numerical simulation of tsunami wave forces impinged on bridge superstructures. Coast Eng 121:145–157

    Google Scholar 

  8. Arabi MG, Sogut DV, Khosronejad A, Yalciner AC, Farhadzadeh A (2019) A numerical and experimental study of local hydrodynamics due to interactions between a solitary wave and an impervious structure. Coast Eng 147:43–62

    Google Scholar 

  9. Xie Z, Stoesser T (2020) Two-phase flow simulation of breaking solitary waves over surface-piercing and submerged conical structures. Ocean Eng 213:107679

    Google Scholar 

  10. Bagherizadeh E, Zhang Z, Farhadzadeh A, Angelidis D, Ghazian Arabi M, Moghimi S, Khosronejad A (2021) Numerical modelling of solitary wave and structure interactions using level-set and immersed boundary methods by adopting adequate inlet boundary conditions. J Hydraul Res 59(4):559–585

    Google Scholar 

  11. Sogut DV, Sogut E, Farhadzadeh A (2021) Interaction of a solitary wave with an array of macro-roughness elements in the presence of steady currents. Coast Eng 164:103829

    Google Scholar 

  12. Sogut E, Sogut DV, Farhadzadeh A (2021) A comparative study of interaction of random waves with a cluster of structures on a berm with rans and les models. Coast Eng 168:103941

    Google Scholar 

  13. Oñate E, Garcıa J (2001) A finite element method for fluid–structure interaction with surface waves using a finite calculus formulation. Comput Methods Appl Mech Eng 191(6–7):635–660

    MATH  Google Scholar 

  14. Wall WA, Genkinger S, Ramm E (2007) A strong coupling partitioned approach for fluid–structure interaction with free surfaces. Comput Fluids 36(1):169–183

    MATH  Google Scholar 

  15. Yan J, Korobenko A, Deng X, Bazilevs Y (2016) Computational free-surface fluid–structure interaction with application to floating offshore wind turbines. Comput Fluids 141:155–174

    MathSciNet  MATH  Google Scholar 

  16. Yan J, Deng X, Korobenko A, Bazilevs Y (2017) Free-surface flow modeling and simulation of horizontal-axis tidal-stream turbines. Comput Fluids 158:157–166

    MathSciNet  MATH  Google Scholar 

  17. Bazilevs Y, Yan J, Deng X, Korobenko A (2019) Computer modeling of wind turbines: 2. Free-surface FSI and fatigue-damage. Arch Comput Methods Eng 26(4):1101–1115

    MathSciNet  Google Scholar 

  18. Yan J, Deng X, Fei X, Songzhe X, Zhu Q (2020) Numerical simulations of two back-to-back horizontal axis tidal stream turbines in free-surface flows. J Appl Mech 87(6)

  19. Chen Z-P, Zhang X, Sze KY, Kan L, Qiu X-M (2018) vp material point method for weakly compressible problems. Comput Fluids 176:170–181

    MathSciNet  MATH  Google Scholar 

  20. Idelsohn SR, Oñate E, Del Pin F, Calvo N (2006) Fluid–structure interaction using the particle finite element method. Comput Methods Appl Mech Eng 195(17–18):2100–2123

    MathSciNet  MATH  Google Scholar 

  21. Yang X, Liu M, Peng S, Huang C (2016) Numerical modeling of dam-break flow impacting on flexible structures using an improved SPH-EBG method. Coast Eng 108:56–64

    Google Scholar 

  22. Khayyer A, Gotoh H, Falahaty H, Shimizu Y (2018) An enhanced ISPH-SPH coupled method for simulation of incompressible fluid-elastic structure interactions. Comput Phys Commun 232:139–164

    MathSciNet  MATH  Google Scholar 

  23. Zhan L, Peng C, Zhang B, Wei W (2019) A stabilized TL-WC SPH approach with GPU acceleration for three-dimensional fluid–structure interaction. J Fluids Struct 86:329–353

    Google Scholar 

  24. Sun PN, Le Touzé D, Zhang A-M (2019) Study of a complex fluid–structure dam-breaking benchmark problem using a multi-phase SPH method with APR. Eng Anal Bound Elem 104:240–258

    MathSciNet  MATH  Google Scholar 

  25. Ng KC, Alexiadis A, Chen H, Sheu TWH (2020) A coupled smoothed particle hydrodynamics-volume compensated particle method (SPH-VCPM) for fluid structure interaction (FSI) modelling. Ocean Eng 218:107923

    Google Scholar 

  26. Sun P-N, Le Touze D, Oger G, Zhang A-M (2021) An accurate FSI-SPH modeling of challenging fluid–structure interaction problems in two and three dimensions. Ocean Eng 221:108552

    Google Scholar 

  27. Khayyer A, Shimizu Y, Gotoh H, Hattori S (2021) Multi-resolution ISPH-SPH for accurate and efficient simulation of hydroelastic fluid–structure interactions in ocean engineering. Ocean Eng 226:108652

    Google Scholar 

  28. O’Connor J, Rogers BD (2021) A fluid–structure interaction model for free-surface flows and flexible structures using smoothed particle hydrodynamics on a GPU. J Fluids Struct 104:103312

    Google Scholar 

  29. Lyu H-G, Sun P-N, Huang X-T, Chen S-H, Zhang A-M (2021) On removing the numerical instability induced by negative pressures in SPH simulations of typical fluid–structure interaction problems in ocean engineering. Appl Ocean Res 117:102938

    Google Scholar 

  30. O’Connor J, Revell A (2019) Dynamic interactions of multiple wall-mounted flexible flaps. J Fluid Mech 870:189–216

    MathSciNet  Google Scholar 

  31. Yang Q, Jones V, McCue L (2012) Free-surface flow interactions with deformable structures using an SPH-FEM model. Ocean Eng 55:136–147

    Google Scholar 

  32. McLoone M, Quinlan NJ (2022) Coupling of the meshless finite volume particle method and the finite element method for fluid–structure interaction with thin elastic structures. Eur J Mech B Fluids 92:117–131

    MathSciNet  MATH  Google Scholar 

  33. Gotoh H, Khayyer A, Shimizu Y (2021) Entirely Lagrangian meshfree computational methods for hydroelastic fluid–structure interactions in ocean engineering-reliability, adaptivity and generality. Appl Ocean Res 115:102822

    Google Scholar 

  34. Khayyer A, Gotoh H, Shimizu Y (2022) On systematic development of FSI solvers in the context of particle methods. J Hydrodyn 34(3):395–407

    Google Scholar 

  35. Cirak F, Deiterding R, Mauch SP (2007) Large-scale fluid–structure interaction simulation of viscoplastic and fracturing thin-shells subjected to shocks and detonations. Comput Struct 85(11–14):1049–1065

    Google Scholar 

  36. Wang KG, Lea P, Farhat C (2015) A computational framework for the simulation of high-speed multi-material fluid–structure interaction problems with dynamic fracture. Int J Numer Methods Eng 104(7):585–623

    MathSciNet  MATH  Google Scholar 

  37. Moutsanidis G, Kamensky D, Chen JS, Bazilevs Y (2018) Hyperbolic phase field modeling of brittle fracture: Part II-immersed IGA–RKPM coupling for air-blast–structure interaction. J Mech Phys Solids 121:114–132

    MathSciNet  Google Scholar 

  38. Behzadinasab M, Moutsanidis G, Trask N, Foster JT, Bazilevs Y (2021) Coupling of IGA and peridynamics for air-blast fluid–structure interaction using an immersed approach. Forces Mech 4:100045

    Google Scholar 

  39. Ni R, Li J, Zhang X, Zhou X, Cui X (2022) An immersed boundary-material point method for shock-structure interaction and dynamic fracture. J Comput Phys 470:111558

    MathSciNet  MATH  Google Scholar 

  40. Rahimi MN, Kolukisa DC, Yildiz M, Ozbulut M, Kefal A (2022) A generalized hybrid smoothed particle hydrodynamics-peridynamics algorithm with a novel Lagrangian mapping for solution and failure analysis of fluid–structure interaction problems. Comput Methods Appl Mech Eng 389:114370

    MathSciNet  MATH  Google Scholar 

  41. Yao X, Huang D (2022) Coupled PD-SPH modeling for fluid–structure interaction problems with large deformation and fracturing. Comput Struct 270:106847

    Google Scholar 

  42. Sun W-K, Zhang L-W, Liew KM (2022) A coupled SPH-PD model for fluid–structure interaction in an irregular channel flow considering the structural failure. Comput Methods Appl Mech Eng 401:115573

    MathSciNet  MATH  Google Scholar 

  43. Ke W, Yang D, Wright N (2016) A coupled SPH-DEM model for fluid–structure interaction problems with free-surface flow and structural failure. Comput Struct 177:141–161

    Google Scholar 

  44. Ng KC, Low WC, Chen H, Tafuni A, Nakayama A (2022) A three-dimensional fluid–structure interaction model based on SPH and lattice-spring method for simulating complex hydroelastic problems. Ocean Eng 260:112026

    Google Scholar 

  45. Yang F, Xin G, Xia X, Zhang Q (2022) A peridynamics-immersed boundary-lattice Boltzmann method for fluid–structure interaction analysis. Ocean Eng 264:112528

    Google Scholar 

  46. Borden MJ, Verhoosel CV, Scott MA, Hughes TJR, Landis CM (2012) A phase-field description of dynamic brittle fracture. Comput Methods Appl Mech Eng 217:77–95

    MathSciNet  MATH  Google Scholar 

  47. Gingold RA, Monaghan JJ (1977) Smoothed particle hydrodynamics: theory and application to non-spherical stars. Mon Not R Astron Soc 181(3):375–389

    MATH  Google Scholar 

  48. Libersky LD, Petschek AG, Carney TC, Hipp JR, Allahdadi FA (1993) High strain Lagrangian hydrodynamics: a three-dimensional SPH code for dynamic material response. J Comput Phys 109(1):67–75

    MATH  Google Scholar 

  49. Monaghan JJ, Kos A (1999) Solitary waves on a cretan beach. J Waterw Port Coast Ocean Eng 125(3):145–155

    Google Scholar 

  50. Vignjevic R, Reveles JR, Campbell J (2006) SPH in a total Lagrangian formalism. CMC-Tech Science Press- 4(3):181

    MathSciNet  MATH  Google Scholar 

  51. Liu MB, Liu GR (2010) Smoothed particle hydrodynamics (SPH): an overview and recent developments. Arch Comput Methods Eng 17(1):25–76

    MathSciNet  MATH  Google Scholar 

  52. Vacondio R, Rogers BD, Stansby PK, Mignosa P, Feldman J (2013) Variable resolution for SPH: a dynamic particle coalescing and splitting scheme. Comput Methods Appl Mech Eng 256:132–148

    MathSciNet  MATH  Google Scholar 

  53. Crespo AJC, Domínguez JM, Rogers BD, Gómez-Gesteira M, Longshaw S, Canelas RJFB, Vacondio R, Barreiro A, García-Feal O (2015) Dualsphysics: Open-source parallel CFD solver based on smoothed particle hydrodynamics (SPH). Comput Phys Commun 187:204–216

    MATH  Google Scholar 

  54. Fourtakas G, Stansby PK, Rogers BD, Lind SJ, Yan S, Ma Q (2018) On the coupling of incompressible SPH with a finite element potential flow solver for nonlinear free-surface flows. Int J Offsh Polar Eng 28(03):248–254

    Google Scholar 

  55. Fourtakas G, Rogers BD, Nasar AMA (2021) Towards pseudo-spectral incompressible smoothed particle hydrodynamics (ISPH). Comput Phys Commun 266:108028

    MathSciNet  MATH  Google Scholar 

  56. King JRC, Lind SJ, Rogers BD, Stansby PK, Vacondio R (2022) Large eddy simulations of bubbly flows and breaking waves with smoothed particle hydrodynamics. arXiv:2206.01641

  57. Feng R, Fourtakas G, Rogers BD, Lombardi D (2022) Two-phase fully-coupled smoothed particle hydrodynamics (SPH) model for unsaturated soils and its application to rainfall-induced slope collapse. Comput Geotech 151:104964

    Google Scholar 

  58. Miehe C, Hofacker M, Welschinger F (2010) A phase field model for rate-independent crack propagation: robust algorithmic implementation based on operator splits. Comput Methods Appl Mech Eng 199(45–48):2765–2778

    MathSciNet  MATH  Google Scholar 

  59. Borden MJ, Hughes TJR, Landis CM, Verhoosel CV (2014) A higher-order phase-field model for brittle fracture: Formulation and analysis within the isogeometric analysis framework. Comput Methods Appl Mech Eng 273:100–118

    MathSciNet  MATH  Google Scholar 

  60. Ambati M, Gerasimov T, De Lorenzis L (2015) A review on phase-field models of brittle fracture and a new fast hybrid formulation. Comput Mech 55(2):383–405

    MathSciNet  MATH  Google Scholar 

  61. Kakouris EG, Triantafyllou SP (2017) Phase-field material point method for brittle fracture. Int J Numer Methods Eng 112(12):1750–1776

    MathSciNet  Google Scholar 

  62. Kamensky D, Moutsanidis G, Bazilevs Y (2018) Hyperbolic phase field modeling of brittle fracture: part I-theory and simulations. J Mech Phys Solids 121:81–98

    MathSciNet  Google Scholar 

  63. Svolos L, Bronkhorst CA, Waisman H (2020) Thermal-conductivity degradation across cracks in coupled thermo-mechanical systems modeled by the phase-field fracture method. J Mech Phys Solids 137:103861

    MathSciNet  Google Scholar 

  64. Kristensen PK, Niordson CF, Martínez-Paneda E (2020) Applications of phase field fracture in modelling hydrogen assisted failures. Theor Appl Fract Mech 110:102837

    Google Scholar 

  65. Cui C, Ma R, Martínez-Pañeda E (2021) A phase field formulation for dissolution-driven stress corrosion cracking. J Mech Phys Solids 147:104254

    MathSciNet  Google Scholar 

  66. Svolos L, Mourad HM, Bronkhorst CA, Waisman H (2021) Anisotropic thermal-conductivity degradation in the phase-field method accounting for crack directionality. Eng Fract Mech 245:107554

    Google Scholar 

  67. Svolos L, Mourad HM, Manzini G, Garikipati K (2022) A fourth-order phase-field fracture model: formulation and numerical solution using a continuous/discontinuous galerkin method. J Mech Phys Solids 165:104910

    MathSciNet  Google Scholar 

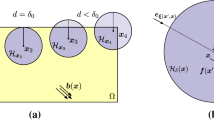
  68. Rahimi MN, Moutsanidis G (2022) A smoothed particle hydrodynamics approach for phase field modeling of brittle fracture. Comput Methods Appl Mech Eng 398:115191

    MathSciNet  MATH  Google Scholar 

  69. Dalrymple RA, Rogers BD (2006) Numerical modeling of water waves with the SPH method. Coast Eng 53(2–3):141–147

    Google Scholar 

  70. Smagorinsky J (1963) General circulation experiments with the primitive equations: I. The basic experiment. Mon Weather Rev 91(3):99–164

    Google Scholar 

  71. Griffith AA (1921) Vi. The phenomena of rupture and flow in solids. Philos Trans R Soc Lond Ser A 221(582–593):163–198

    MATH  Google Scholar 

  72. Bourdin B, Francfort GA, Marigo J-J (2000) Numerical experiments in revisited brittle fracture. J Mech Phys Solids 48(4):797–826

    MathSciNet  MATH  Google Scholar 

  73. Kuhn C, Müller R (2008) A phase field model for fracture. In PAMM: Proceedings in applied mathematics and mechanics, vol 8. Wiley Online Library. p 10223–10224

  74. Rahimi MN, Moutsanidis G (2022) Modeling dynamic brittle fracture in functionally graded materials using hyperbolic phase field and smoothed particle hydrodynamics. Comput Methods Appl Mech Eng 401:115642

    MathSciNet  MATH  Google Scholar 

  75. Monaghan JJ (2005) Smoothed particle hydrodynamics. Rep Prog Phys 68(8):1703–1759

    MathSciNet  MATH  Google Scholar 

  76. Bonet J, Lok TSL (1999) Variational and momentum preservation aspects of Smooth particle hydrodynamic formulations. Comput Methods Appl Mech Eng 180(1–2):97–115

    MathSciNet  MATH  Google Scholar 

  77. Tofighi N, Ozbulut M, Rahmat A, Feng JJ, Yildiz M (2015) An incompressible smoothed particle hydrodynamics method for the motion of rigid bodies in fluids. J Comput Phys 297:207–220

    MathSciNet  MATH  Google Scholar 

  78. Vincent S, Brändle JC, de Motta A, Sarthou J-LE, Simonin O, Climent E (2014) A Lagrangian VOF tensorial penalty method for the DNS of resolved particle-laden flows. J Comput Phys 256:582–614

    MathSciNet  MATH  Google Scholar 

  79. Shadloo MS, Zainali A, Sadek SH, Yildiz M (2011) Improved incompressible smoothed particle hydrodynamics method for simulating flow around bluff bodies. Comput Methods Appl Mech Eng 200(9):1008–1020

    MathSciNet  MATH  Google Scholar 

  80. Ozbulut M, Tofighi N, Goren O, Yildiz M (2017) Investigation of wave characteristics in oscillatory motion of partially filled rectangular tanks. J Fluids Eng 140(4):12

    Google Scholar 

  81. Khayyer A, Shimizu Y, Gotoh T, Gotoh H (2023) Enhanced resolution of the continuity equation in explicit weakly compressible SPH simulations of incompressible free-surface fluid flows. Appl Math Model 116:84–121

    MathSciNet  MATH  Google Scholar 

  82. Belytschko T, Guo Y, Kam Liu W, Ping Xiao S (2000) A unified stability analysis of meshless particle methods. Int J Numer Methods Eng 48(9):1359–1400

    MathSciNet  MATH  Google Scholar 

  83. Swegle JW, Hicks DL, Attaway SW (1995) Smoothed particle hydrodynamics stability analysis. J Comput Phys 116(1):123–134

    MathSciNet  MATH  Google Scholar 

  84. Islam MRI, Peng C (2019) A total Lagrangian SPH method for modelling damage and failure in solids. Int J Mech Sci 157:498–511

    Google Scholar 

  85. Wang L, Fei X, Yang Y (2021) An improved total Lagrangian SPH method for modeling solid deformation and damage. Eng Anal Bound Elem 133:286–302

    MathSciNet  MATH  Google Scholar 

  86. Monaghan JJ, Gingold RA (1983) Shock simulation by the particle method SPH. J Comput Phys 52(2):374–389

    MATH  Google Scholar 

  87. Rahimi MN, Moutsanidis G (2022) A coupled total Lagrangian SPH-phase-field framework for modeling dynamic brittle fracture. In: Giuseppe B (ed) 2022 International SPHERIC work., number June. Catania, Italy. Istituto Nazionale di Geofisica e Vulcanologi. p 71–76

  88. Shimizu Y, Khayyer A, Gotoh H (2022) An implicit SPH-based structure model for accurate fluid–structure interaction simulations with hourglass control scheme. Eur J Mech B Fluids 96:122–145

    MathSciNet  MATH  Google Scholar 

  89. Khayyer A, Shimizu Y, Gotoh H, Nagashima K (2021) A coupled incompressible SPH-Hamiltonian SPH solver for hydroelastic FSI corresponding to composite structures. Appl Math Model 94:242–271

    MathSciNet  MATH  Google Scholar 

  90. Diehl P, Lipton R, Wick T, Tyagi M (2022) A comparative review of peridynamics and phase-field models for engineering fracture mechanics. Comput Mech 69:1259–1293

    MathSciNet  MATH  Google Scholar 

  91. Landau LD, Lifšic EM, Lifshitz EM, Kosevich AM, Pitaevskii LP (1986) Theory of elasticity, vol 7. Elsevier, Amsterdam

    Google Scholar 

  92. Gray JP, Monaghan JJ, Swift RP (2001) SPH elastic dynamics. Comput Methods Appl Mech Eng 190(49):6641–6662

    MATH  Google Scholar 

  93. Monaghan JJ, Rafiee A (2013) A simple SPH algorithm for multi-fluid flow with high density ratios. Int J Numer Methods Fluids 71(5):537–561

    MathSciNet  MATH  Google Scholar 

  94. Antuono M, Marrone S, Colagrossi A, Bouscasse B (2015) Energy balance in the \(\delta\)-SPH scheme. Comput Methods Appl Mech Eng 289:209–226

    MathSciNet  MATH  Google Scholar 

  95. Khayyer A, Gotoh H, Shimizu Y (2017) Comparative study on accuracy and conservation properties of two particle regularization schemes and proposal of an optimized particle shifting scheme in ISPH context. J Comput Phys 332:236–256

    MathSciNet  MATH  Google Scholar 

  96. Lobovský L, Botia-Vera E, Castellana F, Mas-Soler J, Souto-Iglesias A (2014) Experimental investigation of dynamic pressure loads during dam break. J Fluids Struct 48:407–434

    Google Scholar 

  97. Antuono M, Colagrossi A, Marrone S, Molteni D (2010) Free-surface flows solved by means of SPH schemes with numerical diffusive terms. Comput Phys Commun 181(3):532–549

    MathSciNet  MATH  Google Scholar 

  98. Ting TS, Prakash M, Cleary PW, Thompson MC (2006) Simulation of high ||Reynolds number flow over a backward facing step using SPH. In: Stacey A, Blyth B, Shepherd J, Roberts AJ (eds) Proceedings of the 7th biennial engineering mathematics and applications conference, EMAC-2005, volume 47 of ANZIAM J. p C292–C309

  99. Kim J, Kline SJ, Johnston JP (1980) Investigation of a reattaching turbulent shear layer: flow over a backward-facing step. J Fluids Eng 102(3):302–308

    Google Scholar 

  100. Fourey G, Hermange C, Le Touzé D, Oger G (2017) An efficient FSI coupling strategy between smoothed particle hydrodynamics and finite element methods. Comput Phys Commun 217:66–81

    MathSciNet  MATH  Google Scholar 

  101. Stephen T, Sergius W-K et al (1959) Theory of plates and shells, vol 2. McGraw-hill, New York

    Google Scholar 

  102. Li Z, Leduc J, Nunez-Ramirez J, Combescure A, Marongiu JC (2015) A non-intrusive partitioned approach to couple smoothed particle hydrodynamics and finite element methods for transient fluid–structure interaction problems with large interface motion. Comput Mech 55(4):697–718

    MathSciNet  MATH  Google Scholar 

  103. Rafiee A, Thiagarajan KP (2009) An SPH projection method for simulating fluid-hypoelastic structure interaction. Comput Methods Appl Mech Eng 198(33):2785–2795

    MATH  Google Scholar 

  104. Marti J, Idelsohn S, Limache A, Calvo N, D’Elía J (2006) A fully coupled particle method for quasi incompressible fluid-hypoelastic structure interactions. Mecánica Computacional 809–828

Download references

Acknowledgements

The authors would like to thank Stony Brook Research Computing and Cyberinfrastructure, and the Institute for Advanced Computational Science at Stony Brook University for access to the high-performance SeaWulf computing system, which was made possible by a $1.4 M National Science Foundation grant (#1531492).

Author information

Authors and Affiliations

  1. Department of Civil Engineering, Stony Brook University, Stony Brook, NY, 11794, USA

    Mohammad Naqib Rahimi & Georgios Moutsanidis

  2. Institute for Advanced Computational Science, Stony Brook, NY, 11794, USA

    Georgios Moutsanidis

Authors
  1. Mohammad Naqib Rahimi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Georgios Moutsanidis
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Georgios Moutsanidis.

Ethics declarations

Conflict of interest

The authors have no relevant financial or non-financial interests to disclose.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rahimi, M.N., Moutsanidis, G. An SPH-based FSI framework for phase-field modeling of brittle fracture under extreme hydrodynamic events. Engineering with Computers 39, 2365–2399 (2023). https://doi.org/10.1007/s00366-023-01857-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-023-01857-0

Keywords