Skip to main content
Springer Nature Link
Log in

Finding and defining the generators of genus-n objects for constructing topological and cut graphs

  • original article
  • Published:
The Visual Computer Aims and scope Submit manuscript

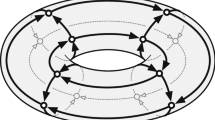
Abstract

The topology of an object is commonly represented through a topological graph or a cut graph (polygonal scheme). Over the past few years, many studies have focused on extracting the topological and cut graphs of complex freeform objects that are represented by meshes. For an object with genus-n, the topological graph has n cycles, while the cut graph contains 2n cycles. These loops, however, do not always explicitly represent the holes in the objects. That is, a cycle in the graph can be a cycle around a solid (meridian), a cycle around a hole (longitude), or almost any combination of the two. The task of classifying the cycles (generators) as cycles around holes (longitude) and cycles around solids (meridians) on the mesh is not straightforward. Every closed orientable 2-manifold with genus-n can be seen as a collection of n toruses stitched together, so that each hole in the object can be referred to as a torus with two generators. This paper proposes a method that extracts the generators from which the longitudes and the meridians are found. The topological graph is defined by the longitudes and by a spanning tree constructed between them. The cut graph is constructed using the same concept. The advantage of the proposed method over other methods is that each loop in the topological graph explicitly represents a hole in the object.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Biasotti S (2001) Topology techniques for shape understanding. In: Proceedings of the Central European seminar on computer graphics (CESCG 2001), Budmerice Castle, Slovakia, 23–25 April 2001, pp 10–14

  2. Cohen-Or D, Sorkine O, Goldenthal R, Lischinski D (2002) Bounded – distortion piecewise mesh parametarization. In: Proceedings of IEEE Visualization’02, Boston, 27 October 2002, pp 355–362

  3. Cormen HT, Leiserson EC, Rivest LR (1998) Introduction to algorithms. MIT Press, Cambridge, MA

  4. DeBerg M, Kreveld MV, Overmars M, Schwarzkof O (1997) Computational geometry, algorithms and applications. Springer, Berlin Heidelberg New York

  5. Dey TK, Guha S (1999) Transforming curves on surfaces. J Comput Sys Sci 58:297–325

    Google Scholar 

  6. Dey TK, Schipper H (1995) A new technique to compute polygonal schema for 2-manifolds with application to null-homotopy detection. Discrete Comput Geom 14:93–110

    Google Scholar 

  7. Fischer A, Manor A, Barhak J (1999) Adaptive parameterization for reconstruction of 3D freeform objects from laser-scanned data. In: Proceedings of IEEE Pacific Graphics ’99, Seoul, Korea, 5–7 October 1999

  8. Floater MS (1997) Parameterization and smooth approximation of surface triangulation. Comput Aided Geom Des 14:231–250

    Google Scholar 

  9. Hatcher A (2000) Algebraic topology. http://www.math.cornell.edu/∼hatcher/

  10. Helio H, Rossignac J, Safanova A, Szymczak A, Tavares G (2002) Edgebreaker: a simple compression for surfaces with handles. In: Proceedings of the 7th ACM conference on solid modeling and application, Saarbrücken, Germany, 17–21 June 2002

  11. Hilaga M, Shinagawa Y, Kohmura T, Kunii TL (2001) Topology matching for fully automatic similarity estimation of 3D shapes. In: Proceedings of SIGGRAPH 2001, San Jose, California, 12–17 August 2001, pp 203–212

  12. Jeff E, Sariel HP (2002) Optimally cutting a surface into a disk. In: Proceedings of the symposium on computational geometry, Barcelona, Spain, 5–7 June 2002

  13. Kartasheva E (1999) Reduction of h-genus polyhedrons topology. Int J Shape Model 5(2):179–194

    Google Scholar 

  14. Kawauchi A (1996) A survey of knot theory. Birkhäuser, Boston

  15. Lazarus F, Verroust A (1999) Level set diagrams of polyhedral objects. In: Proceedings of ACM Solid Modeling ’99, Ann Arbor, MI, June 1999

  16. Lazarus F, Pocchiola M, Vegter G, Verroust A (2001) Computing a canonical polygonal schema of an orientable triangulated surface. In: Proceedings of the 17th ACM annual symposium on computational geometry, Medford, MA, 3–5 June 2001, pp 80–89

  17. Lee Y, Kim HS, Lee S (2001) Parameterization of triangular meshes with virtual boundaries. In: Proceedings of the conference on geometrical modeling and computer graphics, Seoul , Korea, October 2001, pp 105–113

  18. Munkers JR (1984) Elements of algebric topology. Addison-Wesley, Redwood City, CA

  19. Shefer A, de Sturler E (2000) Surface parameterization for meshing by triangulation. In: Proceedings of the 9th international meshing roundtable, New Orleans, 2–5 October 2000, pp 161–172

  20. Shinagawa Y, Kunii LT, Kergosien YL (1991) Surface coding based on Morse theory. IEEE Comput Graph Appl 11(5):66–78

    Google Scholar 

  21. Steiner D, Fischer A (2001) Topology recognition of 3D closed freeform objects based on topological graphs. In: Proceedings of Pacific Graphics, Tokyo, 16–18 October 2001, pp 82–88

  22. Steiner D, Fischer A (2002) Cutting 3D freeform objects with genus-n into one-boundary surface using topological graphs. In: Proceedings of the 7th ACM conference on solid modeling and applications, Saarbrücken, Germany, 17–21 June 2002

  23. Tai C-L, Shinagawa Y, Kunii TL (1998) A Reeb graph-based representation for non-sequential construction of topologically complex shapes. Comput Graph 22(2–3):255–268

    Google Scholar 

  24. Touma C, Gotsman C (1998) Triangle mesh compression. In: Proceedings of Graphics Interface’98, Vancouver, BC, Canada, 18–20 June 1998, pp 26–34

  25. Tutte WT (1963) How to draw a graph. Proc Lond Math Soc 13:743–768

    MATH  Google Scholar 

  26. Ulrike A, Herbert E (1998) Auditory Morse analysis of triangulated manifolds. In: Mathematical visualization, Springer, Berlin Heidelberg New York, pp 223–236

  27. Vegter G, Yap CK (1990) Computational complexity of combinatorial surfaces. In: Proceedings of the 6th annual ACM symposium on computational geometry, Berkeley, CA, 6–8 June 1990, pp 102–111

  28. Xianfeng G, Gortler SJ, Hoppe H (2002) Geometry images. In: Proceedings of SIGGRAPH 2002, San Antonio, 23–25 July 2002, pp 362–371

Download references

Author information

Authors and Affiliations

  1. CMSR Laboratory for Computer Graphics and CAD, Department of Mechanical Engineering, Technion – Israel Institute of Technology, Haifa, 32000, Israel

    D. Steiner & A. Fischer

Authors
  1. D. Steiner
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. A. Fischer
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to D. Steiner.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Steiner, D., Fischer, A. Finding and defining the generators of genus-n objects for constructing topological and cut graphs. Visual Comp 20, 266–278 (2004). https://doi.org/10.1007/s00371-003-0232-0

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00371-003-0232-0

Keywords