Abstract
Chamfering, a mask-driven technique, refers to a process of propagating local distances over an image to estimate a reference metric. Performance of the technique depends on the design of chamfer masks using cost functions. To date, most scholars have been using a mean absolute error and a mean squared error to formulate optimization problems for estimating weights in the chamfer masks. However, studies have shown that these optimization functions endure some potential weaknesses, including biasedness and sensitivity to outliers. Motivated by the weaknesses, the present work proposes an alternative difference function, RLog, that is unbiased, symmetrical, and robust. RLog takes the absolute logarithm of the relative accuracy of the estimated distance to compute optimal chamfer weights. Also, we have proposed an algorithm to map entries of the designed real-valued chamfer masks into integers. Analytical and experimental results demonstrate that chamfering based on our weights generate polygons and distance maps with lower errors. Methods and results of our work may be useful in robotics to address the matching problem.










Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
Song, C., Pang, Z., Jing, X., Xiao, C.: Distance field guided L_1-median skeleton extraction. Vis. Comput. 1–13 (2016). doi:10.1007/s00371-016-1331-z
Saha, P.K., Borgefors, G., di Baja, G.S.: A survey on skeletonization algorithms and their applications. Pattern Recognit. Lett. 76, 3–12 (2016)
Coeurjolly, D., Montanvert, A.: Optimal separable algorithms to compute the reverse Euclidean distance transformation and discrete medial axis in arbitrary dimension. arXiv:0705.3343 (2007)
Maurer, C.R., Qi, R., Raghavan, V.: A linear time algorithm for computing exact Euclidean distance transforms of binary images in arbitrary dimensions. IEEE Trans. Pattern Anal. Mach. Intell. 25(2), 265–270 (2003)
Bailey, D.G.: An efficient Euclidean distance transform. In: International Workshop on Combinatorial Image Analysis, pp. 394–408. Springer (2004). doi:10.1007/978-3-540-30503-3_28
Breu, H., Gil, J., Kirkpatrick, D., Werman, M.: Linear time Euclidean distance transform algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 17(5), 529–533 (1995)
Zhang, H., Xu, M., Zhuo, L., Havyarimana, V.: A novel optimization framework for salient object detection. Vis. Comput. 32, 31–41 (2016)
Weng, Y., Xu, W., Wu, Y., Zhou, K., Guo, B.: 2D shape deformation using nonlinear least squares optimization. Vis. Comput. 22(9–11), 653–660 (2006)
Ding, S., Sheng, B., Xie, Z., Ma, L.: Intrinsic image estimation using near-L_0 sparse optimization. Vis. Comput. 33, 1–15 (2016). doi:10.1007/s00371-015-1205-9
Muñoz, A., Gutierrez, D., Serón, F.J.: Optimization techniques for curved path computing. Vis. Comput. 23(7), 493–502 (2007)
Wang, Z., Bovik, A.C.: Mean squared error: love it or leave it? A new look at signal fidelity measures. IEEE Signal Process. Mag. 26, 98–117 (2009)
Tofallis, C.: A better measure of relative prediction accuracy for model selection and model estimation. J. Oper. Res. Soc. 66(8), 1352–1362 (2015)
Butt, M.A., Maragos, P.: Optimum design of chamfer distance transforms. IEEE Trans. Image Process. 7(10), 1477–1484 (1998)
Grevera, G.J.: Distance transform algorithms and their implementation and evaluation. In: Deformable Models , pp. 33–60. Springer (2007). doi:10.1007/978-0-387-68413-0_2
Liu, W., Jiang, H., Bai, X., Tan, G., Wang, C., Liu, W., Cai, K.: Distance transform-based skeleton extraction and its applications in sensor networks. IEEE Trans. Parallel Distrib. Syst. 24(9), 1763–1772 (2013)
Xu, D., Li, H., Zhang, Y.: Fast and accurate calculation of protein depth by Euclidean distance transform. In: Research in Computational Molecular Biology, pp. 304–316. Springer (2013). doi:10.1007/978-3-642-37195-0_30
Mishchenko, Y.: A fast algorithm for computation of discrete Euclidean distance transform in three or more dimensions on vector processing architectures. Signal Image Video Process. 9, 19–27 (2015)
Salvi, D., Zheng, K., Zhou, Y., Wang, S.: Distance transform based active contour approach for document image rectification. In: Applications of Computer Vision (WACV), 2015 IEEE Winter Conference on IEEE , pp. 757–764 (2015)
Elizondo-Leal, J.C., Parra-González, E.F., Ramírez-Torres, J.G.: The exact Euclidean distance transform: a new algorithm for universal path planning. Int. J. Adv. Robot. Syst. 10, 266 (2013)
Linnér, E., Strand, R.: Anti-aliased Euclidean distance transform on 3D sampling lattices. In: Discrete Geometry for Computer Imagery, pp. 88–98. Springer (2014). doi:10.1007/978-3-319-09955-2_8
Dong, J., Sun, C., Yang, W.: An improved method for oriented chamfer matching. In: Intelligence Science and Big Data Engineering, pp. 875–879. Springer (2013)
Tzionas, D., Gall, J.: A comparison of directional distances for hand pose estimation. In: Pattern Recognition, pp. 131–141. Springer (2013)
Kaliamoorthi, P., Kakarala, R.: Directional chamfer matching in 2.5 dimensions. IEEE Signal Process Lett 20(12), 1151–1154 (2013)
Nguyen, D.T.: A novel chamfer template matching method using variational mean field. In: 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2425–2432. IEEE (2014)
Paglieroni, D.W.: Distance transforms: Properties and machine vision applications. CVGIP Graph. Models Image Process. 54, 56–74 (1992)
Ma, T., Yang, X., Latecki, L.J.: Boosting chamfer matching by learning chamfer distance normalization. In: Computer Vision–ECCV 2010, pp. 450–463. Springer (2010). doi:10.1007/978-3-642-15555-0_33
Thiel, E., Montanvert, A.: Shape splitting from medial lines using the 3–4 chamfer distance. In: Visual Form, pp. 537–546. Springer (1992). doi:10.1007/978-1-4899-0715-8_51
Cuisenaire, O., Macq, B.: Fast Euclidean distance transformation by propagation using multiple neighborhoods. Comput. Vis. Image Underst. 76(2), 163–172 (1999)
Saito, T., Toriwaki, J.I.: New algorithms for Euclidean distance transformation of an n-dimensional digitized picture with applications. Pattern Recognit. 27(11), 1551–1565 (1994)
Shih, F.Y., Wu, Y.T.: Fast Euclidean distance transformation in two scans using a 3\(\times \) 3 neighborhood. Comput. Vis. Image Underst. 93(2), 195–205 (2004)
Verwer, B.J.: Local distances for distance transformations in two and three dimensions. Pattern Recognit. Lett. 12(11), 671–682 (1991)
De Myttenaere, A., Golden, B., Le Grand, B., Rossi, F.: Mean absolute percentage error for regression models. Neurocomputing 192, 38–48 (2016)
Franses, P.H.: A note on the mean absolute scaled error. Int. J. Forecast. 32, 20–22 (2016)
Majidpour, M., Qiu, C., Chu, P., Pota, H.R., Gadh, R.: Forecasting the EV charging load based on customer profile or station measurement? Appl. Energy 163, 134–141 (2016)
Foss, T., Stensrud, E., Kitchenham, B., Myrtveit, I.: A simulation study of the model evaluation criterion MMRE. IEEE Trans. Softw. Eng. 29(11), 985–995 (2003)
Acknowledgements
Funding was provided by China Postdoctoral Science Foundation.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no competing interests.
Appendices
Appendix 1: Existence of maximum in RLog
Recalling the RLog formula in (2.18), we want to show that \(g(\theta )\) contains a global maximum, \(g_m\). From the formula, shifted by \(+2g(\theta )\) for positivity,
and
Equation 7.2 suggests the existence of a maximum in g. Substituting \(g'(\theta )=0\) into (7.1) and solve for \(\theta \), we get the location
on the RLog curve that gives the maximum. Substituting \(\theta =\theta _m\) into the RLog formula yields the maximum value of
Appendix 2: Computation of optimal chamfer weights
For any chamfer mask, optimal weights that control the major error lobe can be computed by considering the conditions \(g_m=-g(0^{\circ })\) and \(u=(\phi -\varphi )v\), where \(\phi \) and \(\varphi \) depend on the kernel size (Table 4). Plugging the conditions into the respective formulas gives
Appendix 3: Detailed derivations of chamfer weights for kernels of order \(2n+3\) (\(n=1,2,\ldots \))
This Appendix provides further details on how to derive high-order chamfer kernels. For demonstration purposes, we design the local weights for \(5\times 5\) and \(7\times 7\) kernels.
1.1 \(5\times 5\) chamfer mask
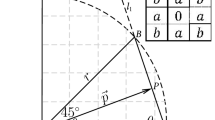
Consider portion of a chamfer polygon, represented by Fig. 4, which contains two sides, namely \(\overline{AB}\) and \(\overline{BC}\). The polygon is inscribed in a disk of radius r, and our goal is to find the maximum possible errors that each side makes relative to its corresponding arc. For the \(5\times 5\) mask, we should compute errors due to \(\overline{AB}\) and due to \(\overline{BC}\); note that errors are zeros when the sides are (ideally) perfectly aligned with the arcs  and
and  , respectively. Adopting notations from the earlier sections, \(f_1(\theta )\) and \(f_2(\theta )\) correspond to the lengths of \(\vec {p}\) from \(\overline{AB}\) and from \(\overline{BC}\), respectively.
, respectively. Adopting notations from the earlier sections, \(f_1(\theta )\) and \(f_2(\theta )\) correspond to the lengths of \(\vec {p}\) from \(\overline{AB}\) and from \(\overline{BC}\), respectively.
The following items give the systematic procedures to compute optimal errors from each polygon’s side generated by a \(5\times 5\) chamfer kernel (refer to Fig. 4 for definitions of variables):
-
(a)
Use the sine rule to find \(f_1(\theta )\) and \(f_2(\theta )\):
$$\begin{aligned} f_1(\theta )=\frac{r\sin \theta _1}{a\sin (\theta +\theta _1)} =\frac{r\sin \theta _1}{a(\sin \theta \cos \theta _1+\cos \theta \sin \theta _1)}. \end{aligned}$$(9.1)and
$$\begin{aligned} f_2(\theta )=\frac{r\sin \theta _2}{a\sin (\theta +\theta _2)}=\frac{r\sin \theta _2}{a(\sin \theta \cos \theta _2+\cos \theta \sin \theta _2)}. \end{aligned}$$(9.2) -
(b)
Use equations of the lines \(l_1\) and \(l_2\), which, respectively, extend \(\overline{AB}\) and \(\overline{BC}\), to define \(\sin \theta _1\), \(\cos \theta _1\), \(\sin \theta _2\), and \(\cos \theta _2\) in (9.1) and (9.2):
$$\begin{aligned} \sin \theta _1=\frac{a}{\sqrt{(c-2a)^2+a^2}},~~ \cos \theta _1=\frac{c-2a}{\sqrt{(c-2a)^2+a^2}}; \end{aligned}$$(9.3)and
$$\begin{aligned} \sin \theta _2= & {} \frac{c-b}{\sqrt{(2b-c)^2+(c-b)^2}},\nonumber \\ \cos \theta _2= & {} \frac{2b-c}{\sqrt{(2b-c)^2+(c-b)^2}} \end{aligned}$$(9.4) -
(c)
Substitute (9.3) into (9.1) and (9.4) into (9.2):
$$\begin{aligned} f_1(\theta )=\frac{r}{(c-2a)\sin \theta +a\cos \theta } \end{aligned}$$(9.5)and
$$\begin{aligned} f_2(\theta )=\frac{r}{(2b-c)\sin \theta +(c-b)\cos \theta }. \end{aligned}$$(9.6) -
(d)
Use the RLog formula to find \(g_1(\theta )\) and \(g_2(\theta )\), which are the respective errors described by \(\vec {p}\) on \(\overline{AB}\) and \(\overline{BC}\):
$$\begin{aligned} g_1(\theta )=\log \left( \frac{1}{r}f_1(\theta )\right) =-\log ((c-2a)\sin \theta +a\cos \theta ) \end{aligned}$$(9.7)and
$$\begin{aligned} g_2(\theta )= & {} \log \left( \frac{1}{r}f_2(\theta )\right) \nonumber \\= & {} -\log ((2b-c) \sin \theta +(c-b)\cos \theta ). \end{aligned}$$(9.8) -
(e)
Identify the polygon’s longest side, which corresponds to the edge that produces the maximum RLog value. From Fig. 4,
$$\begin{aligned} \overline{AB}=\frac{r}{ac}\sqrt{5a^2-4ac+c^2}=r\sqrt{5\left( \frac{a}{c}\right) +\left( \frac{c}{a}\right) -4} \end{aligned}$$(9.9)and
$$\begin{aligned} \overline{BC}= & {} \frac{r}{bc}\sqrt{5b^2-6bc+2c^2}\nonumber \\= & {} r\sqrt{5\left( \frac{b}{c}\right) +2\left( \frac{c}{b}\right) -6}. \end{aligned}$$(9.10)Let \(\phi _1=\frac{c}{a}\) and \(\phi _2=\frac{c}{b}\). If a, b, and c are selected within the allowable limits, then \(\phi _1\ge \phi _2\). Substituting \(\phi _1\) into (9.9) and \(\phi _2\) into (9.10), we have
$$\begin{aligned} \overline{AB}=r\sqrt{\frac{5}{\phi _1}+\phi _1-4} \end{aligned}$$(9.11)and
$$\begin{aligned} \overline{BC}=r\sqrt{\frac{5}{\phi _2}+2\phi _2-6}. \end{aligned}$$(9.12)Evidently, \(\overline{AB}\ge \overline{BC}\) (a typical test can be done using the Euclidean local weights \(a=1\), \(b=\sqrt{2}\), and \(c=\sqrt{5}\)).
-
(f)
\(\overline{AB}\ge \overline{BC}\) implies that \(g_{1m}\ge g_{2m}\), where \(g_{1m}\) and \(g_{2m}\) are the respective peaks for the curves \(g_{1}\) and \(g_{2}\). One strategy to minimize \(g_{1m}\) is to push \(\overline{AB}\) outward in the direction of \(\vec {p}\) such that a triangle extended from \(\triangle OAB\) is isosceles, or \(c=\sqrt{5}a\) and \(-g_1(0^{\circ })=g_{1m}\). Solving the equations gives \(a_{\mathrm {opt}}=0.9865\) and \(c_{\mathrm {opt}}=2.2059\). The value of b should be chosen such that the maximum RLog stays in the range \(0\le g_1(\theta )\le g_{1m}\), and a natural choice is the Euclidean value \(b=\sqrt{2}\).
1.2 \(7\times 7\) chamfer mask
We use Fig. 7 to optimize the local weights in the \(7\times 7\) chamfer mask. Following similar strategies as those used in the case of the \(5\times 5\) mask, the steps are itemized below:
-
(a)
The derived lengths of \(\vec {p}\) on \(\overline{AB}\), \(\overline{BC}\), \(\overline{CD}\), and \(\overline{DE}\) are, respectively,
$$\begin{aligned} f_1(\theta )= & {} \frac{r\sin \theta _1}{a\sin (\theta +\theta _1)}= \frac{r\sin \theta _1}{a(\sin \theta \cos \theta _1+\cos \theta \sin \theta _1)}, \end{aligned}$$(9.13)$$\begin{aligned} f_2(\theta )= & {} \frac{r\sin \theta _2}{a\sin (\theta +\theta _2)}= \frac{r\sin \theta _2}{a(\sin \theta \cos \theta _2+\cos \theta \sin \theta _2)}, \end{aligned}$$(9.14)$$\begin{aligned} f_3(\theta )= & {} \frac{r\sin \theta _3}{a\sin (\theta +\theta _3)}=\frac{r\sin \theta _3}{a(\sin \theta \cos \theta _3+\cos \theta \sin \theta _3)},\nonumber \\ \end{aligned}$$(9.15)and
$$\begin{aligned} f_4(\theta )=\frac{r\sin \theta _4}{a\sin (\theta +\theta _4)}=\frac{r\sin \theta _4}{a(\sin \theta \cos \theta _4+\cos \theta \sin \theta _4)}. \end{aligned}$$(9.16) -
(b)
The trigonometric functions with respect to \(\theta _i\) (\(i=1,2,3,\) and 4) are
$$\begin{aligned} \sin \theta _1= & {} \frac{a}{\sqrt{(d-3a)^2+a^2}}, \end{aligned}$$(9.17)$$\begin{aligned} \cos \theta _1= & {} \frac{d-3a}{\sqrt{(d-3a)^2+a^2}}, \end{aligned}$$(9.18)$$\begin{aligned} \sin \theta _2= & {} \frac{d-c}{\sqrt{(3c-2d)^2+(d-c)^2}}, \end{aligned}$$(9.19)$$\begin{aligned} \cos \theta _2= & {} \frac{3c-2d}{\sqrt{(3c-2d)^2+(d-c)^2}}, \end{aligned}$$(9.20)$$\begin{aligned} \sin \theta _3= & {} \frac{2c-e}{\sqrt{(2e-3c)^2+(2c-e)^2}}, \end{aligned}$$(9.21)$$\begin{aligned} \cos \theta _3= & {} \frac{2e-3c}{\sqrt{(2e-3c)^2+(2c-e)^2}}, \end{aligned}$$(9.22)$$\begin{aligned} \sin \theta _4= & {} \frac{e-2b}{\sqrt{(3b-e)^2+(e-2b)^2}}, \end{aligned}$$(9.23)and
$$\begin{aligned} \cos \theta _4=\frac{3b-e}{\sqrt{(3b-e)^2+(e-2b)^2}}. \end{aligned}$$(9.24) -
(c)
Substitutions of \({\sin \theta _{i}}'s\) and \({\cos \theta _{i}}'s\) into the respective equations for \({f_{i}}'s\) (\(i=1,2,3\) and 4) yield
$$\begin{aligned} f_1(\theta )= & {} \frac{r}{(d-3a)\sin \theta +a\cos \theta }, \end{aligned}$$(9.25)$$\begin{aligned} f_2(\theta )= & {} \frac{r}{(3c-2d)\sin \theta +(d-c)\cos \theta }, \end{aligned}$$(9.26)$$\begin{aligned} f_3(\theta )= & {} \frac{r}{(2e-3c)\sin \theta +(2c-e)\cos \theta }, \end{aligned}$$(9.27)and
$$\begin{aligned} f_4(\theta )=\frac{r}{(3b-e)\sin \theta +(e-2b)\cos \theta }. \end{aligned}$$(9.28) -
(d)
The corresponding RLog formulae are
$$\begin{aligned} \overline{AB}:~g_1(\theta )= & {} \log \left( \frac{1}{r}f_1(\theta )\right) = -\log ((d-3a)\sin \theta \nonumber \\&+a\cos \theta ), \end{aligned}$$(9.29)$$\begin{aligned} \overline{BC}:~g_2(\theta )= & {} \log \left( \frac{1}{r}f_2(\theta )\right) = -\log ((3c-2d)\sin \theta \nonumber \\&+(d-c)\cos \theta ), \end{aligned}$$(9.30)$$\begin{aligned} \overline{CD}:~g_3(\theta )= & {} \log \left( \frac{1}{r}f_3(\theta )\right) = -\log ((2e-3c)\sin \theta \nonumber \\&+(2c-e)\cos \theta ), \end{aligned}$$(9.31)and
$$\begin{aligned} \overline{DE}:~g_4(\theta )= & {} \log \left( \frac{1}{r}f_4(\theta )\right) =-\log ((3b-e)\sin \theta \nonumber \\&+(e-2b)\cos \theta ). \end{aligned}$$(9.32) -
(e)
Comparing the RLog formulae, \(g_1(\theta )\) contains the maximum possible error of \(g_{1m}=-\frac{1}{2}\log ((d-3a)^2+a^2)\), suggesting that \(\overline{AB}\) is the longest side.
-
(f)
Considering the optimality conditions for \(\triangle OAB\), we solve the equations \(d=\sqrt{10}a\) and \(-g_1(0^{\circ })=g_{1m}\). Therefore, the optimal local weights for the \(7\times 7\) chamfer mask are \(a_{\mathrm {opt}}=0.9935\) and \(d_{\mathrm {opt}}=3.1418\). The remaining non-redundant weights should be carefully selected on the condition that RLog on either error lobe stays within the bounds dictated by \(g_{1m}\). And, an obvious selection is the Euclidean local weights \(b=\sqrt{2}\), \(c=\sqrt{5}\), and \(e=\sqrt{13}\).
Rights and permissions
About this article
Cite this article
Maiseli, B.J., Bai, L., Yang, X. et al. Robust cost function for optimizing chamfer masks. Vis Comput 34, 617–632 (2018). https://doi.org/10.1007/s00371-017-1367-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00371-017-1367-8