Skip to main content
Springer Nature Link
Log in

Master-slave hierarchy local information driven fuzzy C-means clustering for noisy image segmentation

  • Original article
  • Published:
The Visual Computer Aims and scope Submit manuscript

Abstract

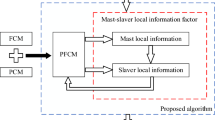
Local neighborhood information plays an important role in robust fuzzy clustering-related segmentation algorithms, and how to construct local information items is the key to robust fuzzy clustering. Based on existing local information constraints, this paper proposes a model to describe the hierarchy relationship of local neighborhood windows in the master–slave neighborhood model, which combines spatial distance with gray information to suppress the influence of noise on current pixel clustering, and can also well control the balance of noise suppression and detail preservation. Based on this model, this paper proposes a robust fuzzy clustering segmentation algorithm with master-slave neighborhood information constraints. When constraining the neighborhood pixels of a pixel (that is the master neighborhood pixels), the algorithm will further constrain the pixels in the neighborhood window around the master neighborhood pixel (that is the salve neighborhood pixels), thus enhancing the robustness of the algorithm. Experiments results show that the proposed algorithm has good segmentation performance and strong anti-noise performance, even significantly outperforms existing state-of-the-art robust fuzzy clustering-related algorithms in the presence of high noise.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Muñoz, X., Freixenet, J., Cufı́, X., Martı́, J.: Strategies for image segmentation combining region and boundary information. Pattern Recognit. Lett. 24(1–3), 375–392 (2003). https://doi.org/10.1016/S0167-8655(02)00262-3

    Article  Google Scholar 

  2. Nida, M.Z., Musbah, J.A.: Survey on image segmentation techniques. Procedia Comput. Sci. 62, 797–806 (2015). https://doi.org/10.1016/j.procs.2015.09.027

    Article  Google Scholar 

  3. Shi, J., Malik, J.: Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 22(8), 888–905 (2000). https://doi.org/10.1109/34.868688

    Article  Google Scholar 

  4. Goyal, S., Kumar, S., Zaveri, M.A., Shukla, A.K.: Fuzzy similarity measure based spectral clustering framework for noisy image segmentation. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 25(4), 649–673 (2017). https://doi.org/10.1142/S0218488517500283

    Article  MathSciNet  Google Scholar 

  5. Gao, X., Zhang, Y., Wang, H., et al.: A modified fuzzy clustering algorithm based on dynamic relatedness model for image segmentation. Vis. Comput. (2022). https://doi.org/10.1007/s00371-022-02430-4

    Article  Google Scholar 

  6. Miloudi, S., Wang, Y., Ding, W.: An improved similarity-based clustering algorithm for multi-database mining. Entropy 23(5), 553 (2021). https://doi.org/10.3390/E23050553

    Article  MathSciNet  Google Scholar 

  7. Fahad, A., Alshatri, N., Tari, Z., Alamri, A., Khalil, I.: A survey of clustering algorithms for big data: taxonomy and empirical analysis. IEEE Trans. Emerg. Top. Comput. 2(3), 267–279 (2014). https://doi.org/10.1109/TETC.2014.2330519

    Article  Google Scholar 

  8. Zhan, K., Nie, F., Wang, J., Yang, Y.: Multiview consensus graph clustering. IEEE Trans. Image Process. 28(3), 1261–1270 (2019). https://doi.org/10.1109/TIP.2018.2877335

    Article  MathSciNet  Google Scholar 

  9. Frey, B.J., Dueck, D.: Clustering by passing messages between data points. Science 315(5814), 972–976 (2007). https://doi.org/10.1126/science.1136800

    Article  MathSciNet  Google Scholar 

  10. Celik, T., Lee, H.K.: Comments on “A robust fuzzy local information c-means clustering algorithm.” IEEE Trans. Image Process. 22(3), 1258–1261 (2013). https://doi.org/10.1109/TIP.2012.2226048

    Article  MathSciNet  Google Scholar 

  11. Nebehay, G., Pflugfelder, R.: Clustering of static-adaptive correspondences for deformable object tracking. In: IEEE Conference on Computer Vision and Pattern Recognition (CVPR). pp. 2784–2791 (2015). https://doi.org/10.1109/CVPR.2015.7298895

  12. Schultz, T., Kindlmann, G.L.: Open-box spectral clustering: applications to medical image analysis. IEEE Trans. Vis. Comput. Graph. 19(12), 2100–2108 (2013). https://doi.org/10.1109/TVCG.2013.181

    Article  Google Scholar 

  13. Noor, S.H., Adnan, M.A., Diyar, Q.Z., Dathar, A.H.: Medical images breast cancer segmentation based on K-means clustering algorithm: a review. Asian J. Res. Comput. Sci. 9(1), 23–38 (2021). https://doi.org/10.9734/AJRCOS/2021/v9i130212

    Article  Google Scholar 

  14. Li, J., Ning, Y., Yuan, Z.M., Yang, C.J.: Research on medical image segmentation based on fuzzy clustering algorithm. Matrix Sci. Pharma. 3(1), 9–11 (2019). https://doi.org/10.4103/MTSP.MTSP_3_19

    Article  Google Scholar 

  15. Anjali, M., Anil, K., Peng, J.: Exploring fuzzy local spatial information algorithms for remote sensing image classification. Remote Sens. 13, 4163 (2021). https://doi.org/10.3390/rs13204163

    Article  Google Scholar 

  16. Jian, J., Wang, K.-L.: A robust nonlocal fuzzy clustering algorithm with between-cluster separation measure for SAR image segmentation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 7(12), 4929–4936 (2014). https://doi.org/10.1109/JSTARS.2014.2308531

    Article  Google Scholar 

  17. Pei, Y., Cai, X., Li, J., Song, K., Liu, R.: Method for identifying the traffic congestion situation of the main road in cold-climate cities based on the clustering analysis algorithm. Sustainability (2021). https://doi.org/10.3390/SU13179741

    Article  Google Scholar 

  18. Han, J., Xu, J., Nie, F., Li, X.: Multi-view k-means clustering with adaptive sparse memberships and weight allocation. IEEE Trans. Knowl. Data Eng. (2015). https://doi.org/10.1109/TKDE.2020.2986201

    Article  Google Scholar 

  19. Liu, X., Zhu, X., Li, M., Zhu, L.E., Liu, T.: Multiple kernel k-means with Incomplete kernels. IEEE Trans. Pattern Anal. Mach. Intell. 42(5), 1191–1204 (2020). https://doi.org/10.1109/TPAMI.2019.2892416

    Article  Google Scholar 

  20. Goyal, S., Kumar, S., Zaveri, M.A., Shukla, A.K.: Fuzzy similarity measure based spectral clustering framework for noisy image segmentation. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 25(4), 649–673 (2017). https://doi.org/10.1142/S0218488517500283

    Article  MathSciNet  Google Scholar 

  21. Sharma, P.K., Holness, G., Markushin, Y., Melikechi, N.: A family of Chisini mean based Jensen-Shannon divergence kernels. In: IEEE 14th International Conference on Machine Learning and Applications. pp. 109–115 (2015). https://doi.org/10.1109/ICMLA.2015.86

  22. Bei, H., Mao, Y., Wang, W., Zhang, X.: Fuzzy clustering method based on improved weighted distance. Math. Probl. Eng. (2021). https://doi.org/10.1155/2021/6687202

    Article  Google Scholar 

  23. Wang, C., Pedrycz, W., Li, Z.W., Zhou, M.C.: Residual-driven fuzzy c-means clustering for image segmentation. IEEE CAA J. Autom. Sin. 8(4), 876–889 (2021). https://doi.org/10.1109/JAS.2020.1003420

    Article  MathSciNet  Google Scholar 

  24. Wang, W., Wang, C., Cui, X., Wang, A.: Improving fuzzy c-means clustering based on adaptive weighting. In: 2008 Fifth International Conference on Fuzzy Systems and Knowledge Discovery. pp. 62–66 (2008). https://doi.org/10.1109/FSKD.2008.160

  25. Bezdek, J.C.: Numerical taxonomy with fuzzy sets. J. Math. Biol. (1974). https://doi.org/10.1007/BF02339490

    Article  MathSciNet  Google Scholar 

  26. Bezdek, J.C., Ehrlich, R., Full, W.: FCM: the fuzzy c-means clustering algorithm. Comput. Geosci. 10(2–3), 191–203 (1984). https://doi.org/10.1016/0098-3004(84)90020-7

    Article  Google Scholar 

  27. Bezdek, J.C., Hathaway, R.J., Sabin, M.J., Tucker, W.T.: Convergence theory for fuzzy c-means: counterexamples and repairs. IEEE Trans. Syst. Man Cybern. 17(5), 873–877 (1987). https://doi.org/10.1109/TSMC.1987.6499296

    Article  Google Scholar 

  28. Ahmed, M.N., Yamany, S.M., Mohamed, N., Farag, A., Moriarty, T.: A modified fuzzy c-means algorithm for bias field estimation and segmentation of MRI data. IEEE Trans. Med. Imag. 21(3), 193–199 (2002). https://doi.org/10.1109/42.996338

    Article  Google Scholar 

  29. Chen, S., Zhang, D.: Robust image segmentation using FCM with spatial constraints based on new kernel-induced distance measure. IEEE Trans. Syst. Man Cybern. Part B Cybern. 34(4), 1907–1916 (2004). https://doi.org/10.1109/TSMCB.2004.831165

    Article  Google Scholar 

  30. Szilagyi, L., Benyo, Z., Szilagyi, S.M., Adam, H.S.: MR brain image segmentation using an enhanced fuzzy C-means algorithm. In: Proceedings of the 25th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. pp. 724–726 (2003). https://doi.org/10.1109/IEMBS.2003.1279866

  31. Cai, W., Chen, S., Zhang, D.: Fast and robust fuzzy c-means clustering algorithms incorporating local information for image segmentation. Pattern Recognit. 40(3), 825–838 (2007). https://doi.org/10.1016/j.patcog.2006.07.011

    Article  Google Scholar 

  32. Krinidis, S., Chatzis, V.: A robust fuzzy local information c-means clustering algorithm. IEEE Trans. Image Process. 19(5), 1328–1337 (2010). https://doi.org/10.1109/TIP.2010.2040763

    Article  MathSciNet  Google Scholar 

  33. Li, N., Huo, H., Zhao, Y., Chen, X., Tao, F.: A spatial clustering method with edge weighting for image segmentation. IEEE Geosci. Remote Sens. Lett. 10(5), 1124–1128 (2013). https://doi.org/10.1109/LGRS.2012.2231662

    Article  Google Scholar 

  34. Zhang, H., Wang, Q., Shi, W., Mao, H.: A novel adaptive fuzzy local information c-means clustering algorithm for remotely sensed imagery classification. IEEE Trans. Geosci. Remote Sens. 55(9), 5057–5068 (2017). https://doi.org/10.1109/TGRS.2017.2702061

    Article  Google Scholar 

  35. Gong, M., Zhou, Z., Ma, J.: Change detection in synthetic aperture radar images based on image fusion and fuzzy clustering. IEEE Trans. Image Process. 21(4), 2141–2151 (2012). https://doi.org/10.1109/TIP.2011.2170702

    Article  MathSciNet  Google Scholar 

  36. Chen, L., Chen Philip, C.L., Lu, M.: A multiple-kernel fuzzy C-means algorithm for image segmentation. IEEE Trans. Syst. Man Cybern. Part B-Cybern. 41(5), 1263–1274 (2011). https://doi.org/10.1109/TSMCB.2011.2124455

    Article  Google Scholar 

  37. Xiang, D., Tang, T., Hu, C., Li, Y., Su, Y.: A kernel clustering algorithm with fuzzy factor: application to SAR image segmentation. IEEE Geosci. Remote Sens. Lett. 11(7), 1290–1294 (2014). https://doi.org/10.1109/LGRS.2013.2292820

    Article  Google Scholar 

  38. Gong, M., Liang, Y., Shi, J., Ma, W., Ma, J.: Fuzzy c-means clustering with local information and kernel metric for image segmentation. IEEE Trans. Image Process. 22(2), 573–584 (2013). https://doi.org/10.1109/TIP.2012.2219547

    Article  MathSciNet  Google Scholar 

  39. Bhagyalakshmi, S., Biju, V.G.: Image segmentation using kernel metric and modified weighted fuzzy factor. Int. J. Eng. Res. Technol. (IJERT) 4(5), 68–71 (2015). https://doi.org/10.17577/IJERTV4IS050183

    Article  Google Scholar 

  40. Hemalatha, K.L., Manvi, S., Suresh, H.N.: Adaptive weighted-covariance regularized kernel fuzzy c means algorithm for medical image segmentation. J. Theor. Appl. Inf. Technol. 95(14), 3365–3375 (2017)

    Google Scholar 

  41. Lu, Z., Qiu, Y., Zhan, T.: Neutrosophic C-means clustering with local information and noise distance-based kernel metric image segmentation. J. Vis. Commun. Image Represent. 58, 269–276 (2019). https://doi.org/10.1016/j.jvcir.2018.11.045

    Article  Google Scholar 

  42. Zhang, X., Guo, Q., Sun, Y., Liu, H., Wang, G., Su, Q., Zhang, C.: Patch-based fuzzy clustering for image segmentation. Soft Comput. 23(3), 3081–3093 (2019). https://doi.org/10.1007/s00500-017-2955-2

    Article  Google Scholar 

  43. Li, M., Xu, L., Gao, S., Xu, N., Yan, B.: Adaptive segmentation of remote sensing images based on global spatial information. Sensors (2019). https://doi.org/10.3390/s19102385

    Article  Google Scholar 

  44. Zhang, X., Sun, Y., Liu, H., Hou, Z., Zhao, F., Zhang, C.: Improved clustering algorithms for image segmentation based on non-local information and back projection. Inf. Sci. 550, 129–144 (2020). https://doi.org/10.1016/j.ins.2020.10.039

    Article  MathSciNet  Google Scholar 

  45. Tang, Y., Ren, F., Pedrycz, W.: Fuzzy c-means clustering through SSIM and patch for image segmentation. Appl. Soft. Comput. (2020). https://doi.org/10.1016/j.asoc.2019.105928

    Article  Google Scholar 

  46. Jia, X., Lei, T., Du, X., Liu, S., Meng, H., Nandi, A.K.: Robust self-sparse fuzzy clustering for image segmentation. IEEE Access 8, 146182–146195 (2020). https://doi.org/10.1109/ACCESS.2020.3015270

    Article  Google Scholar 

  47. Guo, Y., Sengur, A.: A novel color image segmentation approach based on neutrosophic set and modified fuzzy c-means. Circuits Syst. Signal Process. 32(4), 1699–1723 (2013). https://doi.org/10.1007/s00034-012-9531-x

    Article  MathSciNet  Google Scholar 

  48. Lei, T., Jia, X., Zhang, Y., He, L., Meng, H., Nandi, A.K.: Significantly fast and robust fuzzy c-means clustering algorithm based on morphological reconstruction and membership filtering. IEEE Trans. Fuzzy Syst. 26(5), 3027–3041 (2018). https://doi.org/10.1109/TFUZZ.2018.2796074

    Article  Google Scholar 

  49. He, H., Xing, H., Hu, D., Yu, X.: Novel fuzzy uncertainty modeling for land cover classification based on clustering analysis. Sci. China Earth Sci. 62, 438–450 (2018). https://doi.org/10.1007/s11430-017-9224-6

    Article  Google Scholar 

  50. Congalton, R.G.: A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 37, 35–46 (1991). https://doi.org/10.1016/0034-4257(91)90048-B

    Article  Google Scholar 

  51. Fan, J., Zhen, W., Xie, W.: Suppressed fuzzy c-means clustering algorithm. Pattern Recognit. Lett. 24, 1607–1612 (2003). https://doi.org/10.1016/S0167-8655(02)00401-4

    Article  Google Scholar 

  52. Zhao, F., Fan, J., Liu, H.: Optimal-selection-based suppressed fuzzy c-means clustering algorithm with self-tuning non local spatial information for image segmentation. Expert Syst. Appl. 41(9), 4083–4093 (2014). https://doi.org/10.1016/j.eswa.2014.01.003

    Article  Google Scholar 

  53. Wu, C., Liu, N.: Suppressed robust picture fuzzy clustering for image segmentation. Soft Comput. 25, 3751–3774 (2021). https://doi.org/10.1007/s00500-020-05403-8

    Article  Google Scholar 

  54. Liu, B., He, S., He, D., Zhang, Y., Guizani, M.: A spark-based parallel fuzzy c-means segmentation algorithm for agricultural image big data. IEEE Access 7, 42169–42180 (2019). https://doi.org/10.1109/ACCESS.2019.2907573

    Article  Google Scholar 

  55. Jha, P., Tiwari, A., Bharill, N., Ratnaparkhe, M., Mounika, M., Nagendra, N.: Apache Spark based kernelized fuzzy clustering framework for single nucleotide polymorphism sequence analysis. Comput. Biol. Chem. 92, 107475 (2021). https://doi.org/10.1016/j.compbiolchem.2021.107454

    Article  Google Scholar 

  56. https://github.com/lionelee/DIP3E_images

  57. https://www2.eecs.berkeley.edu/Research/Projects/CS/vision/bsds

  58. https://www.kaggle.com/preetviradiya/brian-tumor-dataset

  59. Wang, Q., Wang, X., Fang, C., Yang, W.: Robust fuzzy C-means clustering algorithm with adaptive spatial & intensity constraint and membership linking for noise image segmentation. Appl. Soft. Comput. (2020). https://doi.org/10.1016/j.asoc.2020.106318

    Article  Google Scholar 

  60. Gao, Y., Wang, Z., Xie, J., Pan, J.: A new robust fuzzy c-means clustering method based on adaptive elastic distance. Knowl.-Based Syst. (2022). https://doi.org/10.1016/j.knosys.2021.107769

    Article  Google Scholar 

  61. Wang, Q., Wang, X., Fang, C., Jiao, J.: Fuzzy image clustering incorporating local and region-level information with median memberships. Appl. Soft. Comput. (2021). https://doi.org/10.1016/j.asoc.2021.107245

    Article  Google Scholar 

  62. http://host.robots.ox.ac.uk/pascal/VOC/voc2007/index.html

  63. Zhou, Y., Kwonga, S., Guo, H., Gao, W., Wang, X.: Bilevel optimization of block compressive sensing with perceptually nonlocal similarity. Inf. Sci. 360, 1–20 (2016). https://doi.org/10.1016/j.ins.2016.03.027

    Article  Google Scholar 

  64. Zhou, Y., Guo, H.: Collaborative block compressed sensing reconstruction with dual-domain sparse representation. Inf. Sci. 77, 93 (2019). https://doi.org/10.1016/j.ins.2018.08.064

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Numbers 61671377), and the Natural Science Foundation of Shaanxi Province (2022JM-370). Wu and Wu would like to thank the anonymous reviewers for their constructive suggestions to improve the overall quality of the paper. Besides, Wu and Wu would like to thank the School of Electronic Engineering, Xi’an University of Posts & Telecommunications, Xi’an, China for financial support.

Author information

Authors and Affiliations

  1. School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an, 710121, People’s Republic of China

    Chengmao Wu & Wen Wu

Authors
  1. Chengmao Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Wen Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Wen Wu.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, C., Wu, W. Master-slave hierarchy local information driven fuzzy C-means clustering for noisy image segmentation. Vis Comput 40, 865–897 (2024). https://doi.org/10.1007/s00371-023-02821-1

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00371-023-02821-1

Keywords