Abstract
In the surgery of knee cruciate ligament repair, how to accurately and personalized obtain cruciate ligament insertion centers is the key issue and a great challenge for surgeons. Current artificial judgment is often with deviation, which increases the risk of surgical failure, complications, and the need for a second surgery. Surgical failure can cause imbalanced force on the knee joint (even limping). In this paper, we propose a personalized preoperative positioning method framework of cruciate ligament insertion centers. We focus on locating the insertion centers and verifying the accuracy of the results. The main steps of the method are as follows. First, we propose a new network model W-UNet to better segment accurate bone regions and small ligament regions from MRI. Second, based on RANSAC algorithm and ICP algorithm, MRI bone model and CT bone model are registered. Third, based on the extracted bone and ligament models, we propose an accurate and personalized method for locating the insertion centers. Fourth, we propose a method based on the principle of calculus, using broken lines instead of curves, to solve the problem of ligament reconstruction blocked by intercondylar protrusions. Finally, the length of cruciate ligament with different flexion angles verifies the accuracy of insertion centers. Preoperative personalized insertion centers preoperative positioning can be performed according to the patient’s MRI and CT images. Validation experiments proved the accuracy and robustness of this method. Surgeons can use this framework to accurately obtain personalized preoperative insertion centers location for target patients. This framework provides a reasonable and feasible technical means for locating and marking cruciate ligament insertion centers. It effectively solves the problem of difficult ligament centers localization in clinical surgery and reduces the risk of surgical failure.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Cruciate ligament injury is one of the most common injuries in sports activities or events [1, 2]. Cruciate ligament is an important structure for maintaining the stability of the knee joint. Additionally, with the shape of articular surface and muscles, anterior cruciate ligament and posterior cruciate ligament ensure proper arthrokinematics and play a significant role during passive and active motion [3, 4]. After cruciate ligament injury, it will have a significant impact on patients’ motor function. Most of them cannot run, jump, emergency stop or perform other actions. Cruciate ligament reconstruction aims to restore the biomechanics of the knee joint, so that patients can resume normal movement, reduce the risk of meniscus and articular cartilage injury, and delay the process of knee osteoarthritis [5].
However, at present, there is no effective automatic processing method for personalized preoperative positioning of insertion centers. Most cruciate ligament reconstruction operations are performed according to the experience of surgeons, which requires much professional knowledge [6]. Experience cannot guarantee the accuracy of selected insertion centers, and errors cannot be avoided [7]. If the surgery fails, serious clinical consequences can occur, such as the imbalance of postoperative knee and uninjured knee, knee instability, disability, decreased general health, and the need for secondary operations [8,9,10]. Such operations also have an important influence on the patient’s physical and psychological well-being [11]. In actual clinical treatment, to restore the mechanical properties of knee joint, accurate insertion centers are critical for ligament reconstruction. Improving accuracy of perforation can better restore performance of knee joint. Additionally, locating the perforation position in advance can also reduce the operation time and avoid air infection. In this case, it is still a considerable challenge to develop a more accurate computer-aided personalized insertion centers preoperative positioning method for minimally invasive cruciate ligament reconstruction based on the biological geometric information of the patient’s own uninjured knee. This paper exactly focuses on this key issue.
2 Related works
Computer-aided personalized insertion centers preoperative positioning method for minimally invasive surgery of cruciate ligament reconstruction is an emerging research issue. Consequently, compared to a large amount of research findings on segmentation and extraction of anterior cruciate ligament, there are not many published papers regarding this issue. In this section, we review the existing research works most relevant to our research.
For cruciate ligament segmentation, at present, there are some semi-automatic anterior cruciate ligament segmentation methods. Ho et al. utilized predefined bone and cropping masks in conjunction with active contour [12]. Zarychta et al. proposed using fuzzy C-means (FCM) method to extract anterior and posterior cruciate ligament [13]. These semi-automatic segmentation methods proposed by other scholars (such as Vinay et al. [14,15,16,17,18]) can also accurately segment cruciate ligament and effectively deal with the problem of insufficient data. However, these traditional processing methods rely on image features, while different patients have different image features, and these methods cannot adapt to image changes well. Flannery et al. proposed a transfer learning approach for automatic segmentation of surgically treated anterior cruciate ligament [19, 20]. They used the U-Net network to accurately segment anterior cruciate ligament and adapt to different images [21].
For the registration of MRI bone model and CT bone model, Zheng et al. proposed a feature-based solution for 3D registration of CT and MRI images of a human knee [22]. This method can register a series of CT images with MRI images and obtain good results. However, they do not consider that the patient’s leg with ligament injuries should be tilted when taking MRI images for making it easier to observe the ligament. In this case, sagittal images from MRI and CT cannot be registered. Campanelli et al. proposed a registration method based on fiducial markers implanted in the bone and ICP (iterative closest point) [23]. This method can achieve high registration accuracy between MRI and CT bone models by fixing markers in the knee joint. They also used ICP method to strengthen the registration results. Unfortunately, this method does not very suitable for clinical application, because markers can be fixed arbitrarily on cadaveric bones, but not on patients.
From previous publications we can see there has been no direct study regarding computer-aided personalized insertion centers preoperative positioning method for minimally invasive surgery of cruciate ligament reconstruction. Developing detailed methods for computer-aided personalized insertion centers preoperative positioning is a new research topic. This paper focuses on this challenging issue.
3 Methods
3.1 Overview of our method framework
In this paper, we introduce a recently developed computer-assisted preoperative planning framework for preoperative localization of the cruciate ligament insertion centers. The flowchart of this framework is shown in Fig. 1. Specifically, it contains 3D modeling of CT images, 3D modeling of MRI images, 3D registration of MRI and CT bone models, center location of insertion and verification of results accuracy.
3.2 Segmentation and 3D modeling of cruciate ligament
Our research idea is that, according to cruciate ligament insertion centers on the uninjured side of patient, we can use mirror principle to obtain insertion centers on the injured side. Therefore, the first key step is to accurately extract cruciate ligament on the uninjured side.
To segment cruciate ligament from MRI images, we use transfer learning. Firstly, we use Labelme to label MRI images and establish data sets. The tags are divided into ‘ACL’ (anterior cruciate ligament) and ‘PCL’ (posterior cruciate ligament). Then, we build contracting path and expanding path. Here, to enhance the extraction of image features, we propose a new network structure based on UNet network [21, 24, 25], and we call it W-UNet. The network consists of a dual encoder and a single decoder. We use VGG16 and ResNet50 as two encoders. The network structure is shown in Fig. 2. The configuration information and hyperparameter adjustment details related to the training model are shown in Table 1.
We test different networks with the same data sets and configuration. The results are shown in Tables 2 and 3, and our method has higher segmentation accuracy than other methods and is closest to the ground truth [26,27,28].
Next, we input data sets into the network for training. Because cruciate ligament area is small, the positive and negative samples are unbalanced, cross-entropy loss function cannot be solely used. Here, the combination of dice loss and cross-entropy loss function is used to calculate loss to optimize the network. The formula for dice loss function is
where \({\text{TP}}\), \({\text{FP}}\) and \({\text{ FN}}\) represent the number of true positive, false positive and false negative pixels, respectively. The formula for cross-entropy loss function is
where \(M\) is the number of categories; \(y_{ic}\) is the symbolic function (0 or 1; if the true category of sample \(i\) is equal to \( c\), take 1, otherwise take 0); and \(p_{ic}\) is the prediction probability that the sample \(i\) belongs to category \(c\). The formula for loss function is
Then, we use the trained weights to predict MRI images (as shown in Fig. 3). To obtain more accurate results of insertion centers, three views of MRI images (sagittal plane, coronal plane and cross-sectional plane) are used in combination. The final step is to binarize the segmented MRI images and remove interference points. The cruciate ligament is 3D reconstructed as shown in Fig. 4.
3.3 Segmentation and modeling of femur and tibia
As we know that the bone model modeling effect of CT images is better than that of MRI images, the bone model needs to be reconstructed by CT images of the uninjured side. Firstly, contour of CT cross-sectional images is extracted based on binarization. Next, contour images should fill the contour and remove interference points. Then, 3D CT bone model can be obtained (as shown in Fig. 5).
Obviously, as shown in Fig. 6, the cruciate ligament models cannot be directly fused with the CT bone model. So, MRI bone model is necessary as a bridge to map the cruciate ligament model to the CT bone model. For the bone in MRI images, as with segmenting and modeling the cruciate ligament, we still use the W-UNet network to segment the bone from the sagittal plane, coronal plane and cross-sectional plane of MRI images (as shown in Fig. 7).
Then, the segmented image is processed based on binarization and interference points elimination. Finally, the MRI bone models can be obtained by sagittal plane, coronal plane and cross-sectional plane images, respectively (as shown in Fig. 8).
3.4 Bone models registration between CT and MRI
Although the CT and MRI bone models are obtained, there are some differences, such as shape, spatial location and point distribution (as shown in Table 3 ‘Original’). Cruciate ligament models cannot directly map onto the CT bone model. Registration of the CT bone model and MRI bone models is essential. In our framework, RANSAC (Random Sample Consensus) [29] method is used for coarse registration and ICP (iterative closest point) [30] method is used for fine registration. The registration process is divided into the following steps.
Firstly, registration need to obtain geometric features of the models. However, it is difficult to directly obtain feature information because the shapes of bone models are complicated. An effective method to obtain this information is to use FPFH (Fast Point Feature Histograms) [31]:
where \(k\) is the number of point pairs composed of query point \(p_{q} \) and adjacent point \( p_{k}\). \(w_{k }\) represents the distance between the query point \(p_{q}\) and the adjacent point \( p_{k}\). The characteristic of \(SPFH\) is \( \left\langle {\alpha ,\emptyset ,\theta } \right\rangle\), and the calculation model of characteristic is
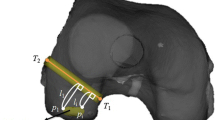
As shown in Fig. 9, this example includes query point \(p_{s}\) and adjacent point \( p_{t}\), where \(n_{s} \) and \(n_{t} \) are the normal vectors of \(p_{s}\) and \( p_{t}, \) respectively.\( \alpha \) represents the angle feature between \(n_{t} \)(yellow arrow) and \(v\) (green arrow). \(\emptyset \) represents the angle feature between the \(u (\) red arrow) and \(p_{s} - p_{t} \)(red line). \(\theta\) represents the angle between the projection of \(n_{t} \) on the \(w - u\) plane and \(u\). The calculation model of a local coordinate system for each set of point pairs \( (u,v,w\)) is
\(u\) and \(n_{s}\) is shown by red arrow. \(v\) is shown by green arrow. \(w\) is shown by blue arrow, and \(n_{t} \) is shown by yellow arrow.
After that, to obtain the coarse registration matrices, RANSAC method and the geometric features obtained are used to register MRI bone models with the CT bone model, respectively.
Finally, ICP method and the coarse registration matrices obtained are used to register the MRI bone models with the CT bone model to achieve fine registration, respectively (as shown in Table 4). It should be emphasized that RANSAC, ICP, and other point cloud registration algorithms are mature algorithms widely used in the fields of computer vision and image processing. They have been studied and optimized for many years, and there is a wealth of literature and open-source implementations available for reference [32,33,34]. Due to the validation and application of RANSAC and ICP algorithms in many related fields, we can trust their effectiveness and reliability in this study. Therefore, in this study, we mainly focus on how to apply these two algorithms to the registration problem of MRI and CT bone models, rather than providing a detailed explanation of their principles and details.
3.5 Extraction of cruciate ligament insertion centers
Upon completion of registration, we have obtained the fine registration matrices mapping cruciate ligament models to the CT bone model. The next step is to obtain the cruciate ligament insertion centers. Firstly, cruciate ligament models are moved onto the CT bone model according to this fine registration matrix (as shown in Fig. 10).
Next, to obtain four different insertion contours (anterior cruciate ligament femur and tibia insertion contours, posterior cruciate ligament femur, and tibia insertion contours), based on the connectivity strategy, CT bone model can be split into femoral model and tibial model (as shown in Fig. 11).
Then, the intersection of cruciate ligament models and CT bone model is used as insertion contours. Approximate insertion centers can be obtained from coordinate means of the four insertion contours. However, insertion contour may have a curved shape, and the approximate insertion center is not on the surface of CT bone model. So, the next step is to use a normal vector to move the approximate center onto the surface. The flowchart is shown in Fig. 12.
We calculate the normal vector mean of the insertion contour points:
where \(\vec{a}\) is the normal vector mean; \(\overrightarrow {{x_{i} }}\) is the normal vector of the insertion contour points; and \(n\) is the number of insertion contour points.
A straight line passing through the CT bone model is generated according to the coordinates of the approximate center points and the normal vector mean. Finally, intersection of the straight line and the CT bone model is final insertion center.
3.6 Reconstruction of cruciate ligament
To verify the accuracy of the insertion centers obtained, we should reconstruct the cruciate ligament and calculate its length. For the anterior cruciate ligament, it is feasible to directly connect the insertion centers to represent the results of anterior cruciate ligament reconstruction. For the posterior cruciate ligament, the same way may cause a part of the posterior cruciate ligament to be blocked by the intercondylar eminence. (When the posterior cruciate ligament and the CT bone model generate two intersections, it is not blocked. Otherwise, it is blocked.) However, this situation does not exist in human body. Therefore, we propose a method to deal with the blocked part. The flowchart is shown in Fig. 13.
Firstly, we move the tibial insertion center point upward and set movement accuracy (1e−5 in our method). Accuracy of movement increases with the center point moving. When there is one intersection between the posterior cruciate ligament and CT bone model, the tibial insertion center point retreats to the previous position. When there are two intersections or the movement accuracy reaches 1e−5, it stops moving to obtain the first tangent point. Then, move the first tangent point in the same way to obtain the second tangent point (as shown in Fig. 14).
Due to the irregular curve of the cruciate ligament attached to the intercondylar protrusion between two tangent points, it is difficult to calculate through some curve calculation formulas. To this end, we propose a method based on the principle of calculus, which uses a series of broken line segments to replace curves. As shown in Fig. 15d, when the folded line segments are small enough, their combination can be seen as a curve. In order to obtain these lines, we did the following:
-
Step 1. Establish a perpendicular line passing through the first tangent point and perpendicular to the two-dimensional image plane (In our method, we use the XY plane), as shown in Fig. 15a;
-
Step 2. Obtain the intersection point between the perpendicular line and the tibial model;
-
Step 3. Calculate the vector from the second tangent to the first tangent, as shown in Fig. 15b;
-
Step 4. Move the above perpendicular line along the vector from the first tangent point to the second tangent point (by 0.01 mm each time in our method), as shown in Fig. 15c;
-
Step 5. Record the intersection point between the vertical line of each movement and the tibial model;
-
Step 6. Connect every two intersection points to obtain a series of broken line segments, as shown in Fig. 15d
We can approximate the combination of these broken line segments as a curve of ligaments attached to the tibia between two tangent points.
Finally, we connect the first tangent point to the femoral insertion center point, the second tangent point to the tibial insertion center point, and every two intersections of the vertical lines and the CT bone model (as shown in Fig. 16).
3.7 Ligament length calculations and verification of insertion centers accuracy
After cruciate ligament reconstruction, to verify the accuracy of insertion centers, the next step is to calculate ligament length. For upright state, we adopt the following procedure.
Because the intercondylar eminence does not block the anterior cruciate ligament, its length can be directly calculated (as shown in Fig. 17). The anterior cruciate ligament length is
where \({ }\left( {x_{1} ,y_{1} ,z_{1} } \right)\) and \(\left( {x_{2} ,y_{2} ,z_{2} } \right)\) represent the point coordinates of tibial and femoral insertion centers of anterior cruciate ligament, respectively.
According to the reconstruction process, length of posterior cruciate ligament must be calculated in three parts (as shown in Fig. 18).
-
Part I: Length between femoral insertion center of posterior cruciate ligament and the first tangent point.
-
Part II: Length between the first tangent point and the second tangent point.
-
Part III: Length between tibial insertion center of posterior cruciate ligament and the second tangent point.
For Part I and Part III, the same way as the anterior cruciate ligament length calculation is used to obtain \(d_{{{\text{pcl}}_{{1}} }}\) and \(d_{{{\text{pcl}}_{{2}} }}\). For Part II, we should use the curve length calculation method for the cruciate ligament blocked by intercondylar eminence. However, the curve is irregular and difficult to be expressed in functional form. So tiny polylines instead of curves are used to approximately express and reconstruct Part II cruciate ligament. When the curve is divided into enough polylines, the length of each polyline is approximately equal to the curve length of this part. Referring to the principle of calculus, the length of Part II can be expressed as
where \({ }\left( {x_{{{\text{i}} + 1}} ,y_{{{\text{i}} + 1}} ,z_{{{\text{i}} + 1}} } \right)\) and \(\left( {x_{{\text{i}}} ,y_{{\text{i}}} ,z_{{\text{i}}} } \right),\) respectively, represent two endpoint coordinates of the \({\text{ith}}\) polyline.
Therefore, overall length of the posterior cruciate ligament is
Based on above way, we can calculate cruciate ligament under different flexion angles. However, there are not corresponding MRI images for CT images with different flexion angles, so using cruciate ligaments in upright state to deform to different flexion angles state is essential. To achieve this goal, the following steps are needed.
Firstly, after obtaining CT bone models with different flexion angles (as shown in Fig. 19), femoral and tibial models are registered with the flexed joint model, respectively (as shown in Table 5). Then, according to the registration transformation matrix, insertion center of upright state is transformed and reconstructed (as shown in Fig. 20). Finally, using above formula for calculating the length of cruciate ligament, we can obtain the results of cruciate ligament length with different flexion angles.
From the results of cruciate ligament length in Table 6, we can see that the largest length of anterior cruciate ligament (ACL) is 25.759 mm (flexion angle = 0°). It is basically isometric (20.0 ± 1.0) mm at 30°, 60°, and 90°. The measurement results of anterior cruciate ligament are within the length variation range of human knee flexion: 0° is (26.1 ± 4.8) mm, and 30°, 60°, and 90° are (23.9 ± 4.5) mm [35]. Posterior cruciate ligament (PCL) becomes longer with increase in flexion angle, and the minimum length is 29.2 mm (flexion angle = 0°). Length of posterior cruciate ligament is also within normal variation range [36]. So, it can be proved that by our method the reconstruction effect of cruciate ligament is satisfactory and the extraction of insertion centers are accurate.
4 Experimental results and evaluation
On the basis of our method in this paper, a software system, which we named it ‘Preoperative planning of cruciate ligament reconstruction’ (Version 1.0), was designed. It was developed based on PyQt5-5.15.4, VTK-9.0.1 (Visualization Toolkit) and OpenCV-4.5.3.56 (Open-Source Computer Vision Library). The system interface is shown in Fig. 21.
To verify the accuracy and robustness of our proposed method, three experiments (Visual verification of insertion centers, length verification of cruciate ligament, symmetry verification) were performed. In these experiments, eight groups of knee joint images (CT manufacturer and model: Neusoft, NeuViz Prime CT; MRI manufacturer and model: Neusoft, NSM-S15P) of healthy volunteers were utilized. Each volunteer’s left leg was considered as healthy leg, and the right leg was considered as injured leg.
4.1 Experimental data disclosure
The dataset used in this chapter was collected from images taken at the Second Affiliated Hospital of Dalian Medical University, with a total of 10,120 images collected. The dataset types include CT images and MRI images. For MRI imaging, collect three views of the left or right knee joint of 8 volunteers at a flexion angle of 0° each time. For CT images, cross-sectional images of the left and right knee joints were collected from 8 volunteers at different flexion angles each time. The information related to the size of the dataset and the collected dataset is shown in Table 7 (param1: Spacing Between Slices, param2: Pixel Spacing).
Due to volunteer privacy issues, the volunteer’s information we can disclose is limited, as shown in Table 8.
With the consent of volunteers, we semi publicly released the dataset (scholars can obtain it by contacting the author’s email, provided that they also follow the same ethical standards and obtain necessary permission from volunteers and institutions). We remove or anonymize all volunteer identifiers before sharing the dataset in accordance with ethical guidelines and regulations.
4.2 Visual verification of insertion centers
The feasibility verification process of our framework is from coarse to fine perspectives. In the first one—visual validation, we assessed whether our framework could achieve the extraction of insertion centers and whether there were mistakes.
As shown in Fig. 22, the insertion centers of eight left knee joints were extracted. After identification by professional surgeons (Joint Surgery, The Second Affiliated Hospital of Dalian Medical University), the positions of insertion centers were correct, and no obvious errors were found.
4.3 Length verification of cruciate ligament
To further verify the accuracy of insertion center position, length verification of cruciate ligament experiments was implemented. In this experiment, we firstly reconstructed the cruciate ligament of the eight knee joints (as shown in Table 9). Then, the femur and tibia in the upright position (flexion angle = 0°) were, respectively, registered with the femur and tibia at other angles, and the registration results are shown in Table 10. Finally, ligament lengths of eight knee joints under different flexion angles were calculated, and the results are shown in Table 11. We can see that the average lengths of cruciate ligament are different for different knee joints, but they are in normal variation range. Anterior cruciate ligaments of eight knee joints are of equal length (except flexion angle = 0°), and posterior cruciate ligaments lengthen with increase in flexion angle. They conform to the length properties and kinematic properties of the knee ligaments [35, 36].
4.4 Symmetry verification
In real life, due to the severe rupture of the cruciate ligament on the injured side of some patients, which is not even attached to bone tissue, it is impossible to extract the insertion centers through the cruciate ligament and achieve precise positioning. For the computer-aided cruciate ligament reconstruction surgery framework proposed in this paper, we proposed using MRI images of the knee joint on the patient’s healthy side to obtain the insertion centers of the knee joint on the patient’s injured side through mirroring. To verify the feasibility and accuracy of this idea, symmetry verification was also implemented. First, the experimental left leg was assumed to be the healthy side and the experimental right leg was assumed to be the injured side. Then, insertion centers of left leg and right leg were extracted by the method in this paper. Finally, insertion centers of left leg were mirrored onto right leg (as shown in Fig. 23). Differences between the symmetry centers and the insertion centers of right leg were calculated. As shown in Table 12, the geometric error fluctuations are both small (Average: 1.493 mm, Variance: 0.411 mm). Therefore, it can be proved that obtaining insertion centers of injured side knee joint by our proposed method is reasonably feasible.
5 Discussion
As a new research topic, computer-aided personalized insertion centers preoperative positioning method for minimally invasive surgery of cruciate ligament reconstruction have made continuous progress in the past few years. The main contribution is that some researchers have proposed effective extraction methods of anterior cruciate ligament [12,13,14,15,16,17,18,19,20]. However, these methods can provide only a little bit help for cruciate ligament reconstruction surgery, and there is a lack of extraction methods of posterior cruciate ligament [37, 38]. As far as we know, there is no similar research report specially on computer-assisted human knee cruciate ligament reconstruction, and few relevant studies have been published. For how to extract cruciate ligament insertion centers, no detailed technical calculation process has been retrieved
Although our framework can support computer-assisted cruciate ligament reconstruction, there are still many challenges in real surgery. One of the limitations is the hardware system. At present, no specific machine can register and track the 3D model obtained based on the software system with the patient entity in surgery. In the future, we plan to purchase a near-infrared optical positioning system, design and develop special equipment to achieve the registration and tracking of virtual 3D model and real patient’s knee joint [39,40,41].
Additionally, another problem is that the system does not consider the injury of patellar ligament, medial collateral ligament and lateral collateral ligament [42,43,44]. In the future, we will also design extraction methods of these three ligaments to improve the system. Meanwhile, we will further communicate with surgeons to continuously improve the system in practical clinical treatment.
6 Conclusions
Researchers are committed to developing minimally invasive, accurate and personalized surgical schemes for cruciate ligament reconstruction surgery. To reconstruct the common clinical ligament rupture, we design an automatic personalized cruciate ligament insertion centers extraction framework. In this framework, a W-UNet model is proposed to achieve the precise extraction of cruciate ligament; the registration between bone models utilizes RANSAC algorithm and ICP algorithm; we also propose an innovative method for locating the center of insertion based on bone and ligament models; and to verify the accuracy of the results, we used the biological characteristics of the ligament and proposed to calculate the length of the ligament obstructed by the intercondylar protrusion based on the principle of calculus. By using the designed framework, we can extract the accurate and personalized insertion centers of injured side knee joint according to the images of patient’s healthy side knee joint, solving the problems of difficult center positioning of clinical surgical discontinuation points and high surgical risks. Through three verification experiments (visual verification of insertion centers, length verification of cruciate ligament, and symmetry verification), the rationality and feasibility of the framework are positive. If there is a near-infrared optical positioning system in the future, surgeons can provide minimally invasive, accurate, and personalized treatment for patients with cruciate ligament rupture.
Data Availability Statement
The datasets generated during the current study are available from the corresponding author on reasonable request.
References
Razali, M. H., Sazwan, S. M., Mahmood, M., et al.: Anterior cruciate ligament (ACL) coronal view injury diagnosis system using convolutional neural network. In: Proceedings of the 2019 2nd International Conference on Electronics and Electrical Engineering Technology, pp 118–122, 2019.
Prince, M.R., Stuart, M.J., King, A.H., et al.: All-inside posterior cruciate ligament reconstruction: Graftlink technique. Arthrosc. Tech. 4(5), e619–e624 (2015)
Rao, Z., Zhou, C., Kernkamp, W.A., et al.: In vivo kinematics and ligamentous function of the knee during weight-bearing flexion: an investigation on mid-range flexion of the knee. Knee Surg. Sports Traumatol. Arthrosc. 28(3), 797–805 (2019)
Krogsgaard, M.R., Fischer-Rasmussen, T., Dyhre-Poulsen, P.: Absence of sensory function in the reconstructed anterior cruciate ligament. J. Electromyogr. Kinesiol. 21(1), 82–86 (2011)
Lynch, T.S., Parker, R.D., Patel, R.M., et al.: The Impact of the Multicenter Orthopaedic Outcomes Network (MOON) research on anterior cruciate ligament reconstruction and orthopaedic practice. J. Am. Acad. Orthop. Surg. 23(3), 154–163 (2015)
Tiamklang, T., Sumanont, S., Foocharoen, T., et al. Double-bundle versus single-bundle reconstruction for anterior cruciate ligament rupture in adults. Cochrane Database Systematic Rev. 11(11), :CD008413 (2012).
Munch, D., Hansen, T.I., Mikkelsen, K.L., et al.: Complications and technical failures are rare in knee ligament reconstruction: analyses based on 31,326 reconstructions during 10 years in Denmark. Knee Surg. Sports Traumatol. Arthrosc. 27(8), 2672–2679 (2019)
Marchant, B.G., Noyes, F.R., Barber-Westin, S.D., et al.: Prevalence of nonanatomical graft placement in a series of failed anterior cruciate ligament reconstructions. Am. J. Sports Med. 38(10), 1987–1996 (2010)
Kohn, D., Rupp, S.: Strategies for revision anterior cruciate ligament reconstruction. Chirurg 71(9), 1055–1065 (2000)
Weiler, A., Jung, T.M., Lubowicki, A., et al.: Management of posterior cruciate ligament reconstruction after previous isolated anterior cruciate ligament reconstruction. Arthroscopy J. Arthroscopic Related Surg. 23(2), 164–169 (2007)
Christino, M.A., Fantry, A.J., Vopat, B.G.: Psychological aspects of recovery following anterior cruciate ligament reconstruction. J. Am. Acad. Orthop. Surg. 23(8), 501 (2015)
Jia, H. H., Wen, Z. L., Seah, C. L., et al. Anterior cruciate ligament segmentation: using morphological operations with active contour. In: 2010 4th International Conference on Bioinformatics and Biomedical Engineering, pp 2209–2212, 2010.
Zarychta, P.: ACL and PCL of the knee joint in the computer diagnostics. In: 21st International Conference "Mixed Design of Integrated Circuits and Systems" (MIXDES 2014), pp 489–492, 2014.
Vinay, N. A,, Vinay, H. C., Narendra, T. V.: An active contour method for mr image segmentation of anterior cruciate ligament (ACL). In: 2014 Fifth international conference on signal and image processing (ICSIP 2014), pp 142–147, 2014.
Lee, H., Hong, H., et al.: Anterior cruciate ligament segmentation from knee MR images using graph cuts with shape priors. J. KISS: Softw. Appl. 41(1), 36–45 (2014)
Lee, H., Hong, H., et al.: Anterior cruciate ligament segmentation from knee MR images using graph cuts with geometric and probabilistic shape constraints. In: Proceedings of the 11th Asian conference on Computer Vision—Volume Part II. 2012:305–315, 2015.
Lee, H., Hong, H., et al.: Segmentation of anterior cruciate ligament in knee MR images using graph cuts with patient-specific shape constraints and label refinement. Comput. Biol. Med. 55, 1–10 (2014)
Gudodagi, R.: Segmentation of ACL in MR images. Int. J. Eng. Comp. Sci. 2(6), 2033–2036 (2013)
Flannery, S.W., Kiapour, A.M., Edgar, D.J., et al.: A transfer learning approach for automatic segmentation of the surgically treated anterior cruciate ligament. J. Orthop. Res. 40(1), 277–284 (2021)
Flannery, S.W., Kiapour, A.M., Edgar, D.J., et al.: Automated magnetic resonance image segmentation of the anterior cruciate ligament. J. Orthop. Res. 39(4), 831–840 (2020)
Ronneberger, O., Fischer, P., Brox, T.: U-Net: Convolutional Networks for Biomedical Image Segmentation. Med. Image Comp. Comp.-Assist. Intervent, pp 234–241, 2015.
Zheng, J., Ji, Z., Yu, K., et al.: A feature-based solution for 3D registration of CT and MRI images of human knee. SIViP 9(8), 1815–1824 (2015)
Campanelli, V., Howell, S.M., Hull, M.L.: Morphological errors in 3D bone models of the distal femur and proximal tibia generated from magnetic resonance imaging and computed tomography determined using two registration methods. Comp. Methods Biomech. Biomed. Eng. Imag. Visualization 8(1), 31–39 (2019)
Yang, D., Chen, N., Tang, Q., et al.: Research on defect detection of toy sets based on an improved U-Net. Vis. Comput. (2023). https://doi.org/10.1007/s00371-023-02834-w
Üzen, H., Turkoglu, M., Aslan, M., et al.: Depth-wise squeeze and excitation block-based efficient-unet model for surface defect detection. Vis. Comput. 39, 1745–1764 (2023)
Strudel, R., Garcia, R., Laptev, I., Schmid, C.: Segmenter: Transformer for Semantic Segmentation. In: IEEE/CVF International Conference on Computer Vision, pp 7242–7252, 2021.
Fu, J., Liu, J., Tian, H., et al.: Dual attention network for scene segmentation. In: IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp 3146–3154, 2019.
Azad, R., Asadi-Aghbolaghi, M., Fathy, M., Escalera, S.: Bi-directional ConvLSTM U-Net with densley connected convolutions. In: IEEE/CVF International Conference on Computer Vision Workshops, pp 27–28, 2019.
Fischler, M.A., Bolles, R.C.: Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 24(6), 381–395 (1981)
Besl, P.J., Mckay, H.D.: A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 14(2), 239–256 (1992)
Rusu, R.B., Blodow, N., Beetz, M.: Fast Point Feature Histograms (FPFH) for 3D registration. In: IEEE International Conference on Robotics and Automation, pp 3212–3217 (2009)
Wang, C., Xu, Y., Wang, L., et al.: Fast structural global registration of indoor colored point cloud. Vis. Comput. 38, 4279–4290 (2022)
Dong, K., Gao, S., Xin, S., et al.: Probability driven approach for point cloud registration of indoor scene. Vis. Comput. 38, 51–63 (2022)
Tao, W., Hua, X., He, X., et al.: Automatic multi-view registration of point clouds via a high-quality descriptor and a novel 3D transformation estimation technique. Vis. Comput. (2023). https://doi.org/10.1007/s00371-023-02942-7
Sun, X.B., Zhang, K.Y., Gang, L.I., et al.: Measurement of anatomical sites to locate the center of reconstruction of the anterior cruciate ligament of knee flexion angle ligament length and its significance. China J. Endosc. 46(4), 453–455 (2014)
Rong, K., Wang, H.P., Wang, Y., et al.: 3D dynamic research on spatial lengths of functional bundles in knee cruciate ligaments. J. Med. Biomech. 29(4), 339–345 (2014)
Choi, H.F., Chincisan, A., Becker, M., et al.: Multimodal composition of the digital patient: a strategy for the knee articulation. Vis. Comput. 30, 739–749 (2014)
Rasool, S., Sourin, A.: Image-driven virtual simulation of arthroscopy. Vis. Comput. 29, 333–344 (2013)
Lin, Q., Yang, R., Cai, K., et al.: Strategy for accurate liver intervention by an optical tracking system. Biomed. Opt. Express 6(9), 3287–3302 (2015)
Zheng, L., Wu, H., Yang, L., et al.: A novel respiratory follow-up robotic system for thoracic-abdominal puncture. IEEE Trans. Industr. Electron. 68(3), 2368–2378 (2021)
Gulabi, D., Erdem, M., et al.: Neglected patellar tendon rupture with anterior cruciate ligament rupture and medial collateral ligament partial rupture. Acta Orthopaedica Et Traumatol. Turcica, 48(2), 231–235 (2014).
Lin, Q., Cai, K., Yang, R., et al.: Development and validation of a near-infrared optical system for tracking surgical instruments. J. Med. Syst. 40(4), 107 (2016)
Jacobson, K.E., Chi, F.S.: Evaluation and treatment of medial collateral ligament and medial-sided injuries of the knee. Sports Med. Arthrosc. Rev. 14(2), 58–66 (2006)
Grawe, B. S. et al.: Lateral collateral ligament injury about the knee: anatomy, evaluation, and management. J. Am. Acad. Orthop. Surg. 26(6), e120–e127 (2018)
Acknowledgements
This study was supported by the National Natural Science Foundation of China (Nos. 62372079, 61972440 and 61572101), the Fundamental Research Funds for the Central Universities of China (No. DUT22YG104), the National Natural Science Foundation of Liaoning Province of China (No. 2021-YGJC-23), the Scientific Research Project of Educational Department of Liaoning Province of China (No. LZ2020031), and the Key Research and Development Projects of Liaoning Province of China (No. 2021JH2/10300025). The author would like to thank the volunteers for providing images.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The author declares that there are no conflicts of interest related to this paper. The authors declare that they have no financial or personal relationship with other persons or organizations that may have an undue impact on their work.
Ethics Approval Statement
All procedures carried out in studies involving human participants comply with the ethical standards of institutions and/or national research committees, as well as the 1964 Declaration of Helsinki and its subsequent amendments or similar ethical standards. All individuals involved in the study obtained informed consent.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Supplementary file1 (MP4 44425 KB)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Liu, H., Li, P., Liu, D. et al. A personalized insertion centers preoperative positioning method for minimally invasive surgery of cruciate ligament reconstruction. Vis Comput 40, 3937–3960 (2024). https://doi.org/10.1007/s00371-024-03399-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00371-024-03399-y