Skip to main content
Springer Nature Link
Log in

Learning microstructure–property mapping via label-free 3D convolutional neural network

  • Original article
  • Published:
The Visual Computer Aims and scope Submit manuscript

Abstract

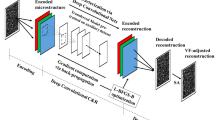
Predicting the physical property of a class of microstructures is crucial in material design, structural simulation, and design. Property prediction may be conducted millions of times in these studies and is better derived instantly for computational efficiency. This issue is addressed in this study via building a mapping from a 3D microstructure to its effective material property, or called structure–property mapping, using a 3D convolutional neural network (CNN). Unlike the direct approach using labeled simulation data, the mapping is based on the physical knowledge of the structure–property relationship determined by its underlying PDE equations. The knowledge is embedded in the loss function of the CNN framework, which is designed and tested under several different formulations to improve its training convergence. Ultimately, the derived structure–property mapping can instantly predict the associated material property for a given microstructure and has far better generalization ability than the data-labeled approach, as demonstrated via numerical examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

Data will be available upon request.

References

  1. Sun, B., Yan, X., Liu, P., Xia, Y., Lu, L.: Parametric plate lattices: modeling and optimization of plate lattices with superior mechanical properties. Addit. Manufact. 72, 103626 (2023)

    Google Scholar 

  2. Zhao, D., Gu, T.T., Liu, Y., Gao, S., Li, M.: Constructing self-supporting structures in biscale topology optimization. Vis. Comput. 38(3), 1065–1082 (2022)

    Google Scholar 

  3. Xu, H., Liu, R., Choudhary, A., Chen, W.: A machine learning-based design representation method for designing heterogeneous microstructures. J. Mech. Design 137(5), 051403 (2015)

    Google Scholar 

  4. Golovin, I.S., Sinning, H.R.: Damping in some cellular metallic materials. J. Alloy. Compd. 355(1), 2–9 (2003)

    Google Scholar 

  5. Garmestani, H., Lin, S., Adams, B., Ahzi, S.: Statistical continuum theory for large plastic deformation of polycrystalline materials. J. Mech. Phys. Solids 49(3), 589–607 (2001)

    Google Scholar 

  6. Raissi, M., Perdikaris, P., Karniadakis, G.E.: Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707 (2019)

    MathSciNet  Google Scholar 

  7. Liu, Y., Greene, M.S., Chen, W., Dikin, D.A., Liu, W.K.: Computational microstructure characterization and reconstruction for stochastic multiscale material design. Comput. Aided Des. 45(1), 65–76 (2013)

    Google Scholar 

  8. Yang, Z., Yabansu, Y.C., Al-Bahrani, R., Liao, W.-K., Choudhary, A.N., Kalidindi, S.R., Agrawal, A.: Deep learning approaches for mining structure-property linkages in high contrast composites from simulation datasets. Comput. Mater. Sci. 151, 278–287 (2018)

    Google Scholar 

  9. Cecen, A., Dai, H., Yabansu, Y.C., Kalidindi, S.R., Song, L.: Material structure-property linkages using three-dimensional convolutional neural networks. Acta Mater. 146, 76–84 (2018)

    Google Scholar 

  10. Chen, D., Levin, D.I., Sueda, S., Matusik, W.: Data-driven finite elements for geometry and material design. ACM Trans. Graph. (TOG) 34(4), 1–10 (2015)

    Google Scholar 

  11. Tan, S., Wong, T., Zhao, Y., Chen, W.: A constrained finite element method for modeling cloth deformation. Vis. Comput. 15, 90–99 (1999)

    Google Scholar 

  12. Conde-Rodríguez, F., Torres, J.-C., García-Fernández, Á.-L., Feito-Higueruela, F.-R.: A comprehensive framework for modeling heterogeneous objects. Vis. Comput. 33, 17–31 (2017)

    Google Scholar 

  13. Xia, L., Raghavan, B., Breitkopf, P., Zhang, W.: A POD/PGD reduction approach for an efficient parameterization of data-driven material microstructure models. Comput. Methods Mater. Sci. 13(1–3), 219–225 (2013)

    Google Scholar 

  14. Nesme, M., Kry, P.G., Jeřábková, L., Faure F.: Preserving topology and elasticity for embedded deformable models, in: ACM SIGGRAPH 2009 papers, pp. 1–9, (2009)

  15. Kharevych, L., Mullen, P., Owhadi, H., Desbrun, M.: Numerical coarsening of inhomogeneous elastic materials. ACM Trans. Graphics (TOG) 28(3), 1–8 (2009)

    Google Scholar 

  16. Torres, R., Rodríguez, A., Espadero, J.M., Otaduy, M.A.: High-resolution interaction with corotational coarsening models. ACM Trans. Graph. 35(6), 1–11 (2016)

    Google Scholar 

  17. Chen, J., Bao, H., Wang, T., Desbrun, M., Huang, J.: Numerical coarsening using discontinuous shape functions. ACM Trans. Graph. (TOG) 37(4), 1–12 (2018)

    Google Scholar 

  18. Fang, Z., Starly, B., Sun, W.: Computer-aided characterization for effective mechanical properties of porous tissue scaffolds. Comput. Aided Des. 37(1), 65–72 (2005)

    Google Scholar 

  19. Kröner E.: Statistical modelling, in: Modelling small deformations of polycrystals, Springer, pp. 229–291, (1986)

  20. Torquato, S., Haslach, H., Jr.: Random heterogeneous materials: microstructure and macroscopic properties. Appl. Mech. Rev. 55(4), B62–B63 (2002)

    Google Scholar 

  21. Michel, J.-C., Moulinec, H., Suquet, P.: Effective properties of composite materials with periodic microstructure: a computational approach. Comput. Methods Appl. Mech. Eng. 172(1–4), 109–143 (1999)

    MathSciNet  Google Scholar 

  22. Liu, X., Shapiro, V.: Homogenization of material properties in additively manufactured structures. Comput. Aided Des. 78, 71–82 (2016)

    Google Scholar 

  23. White, D.A., Arrighi, W.J., Kudo, J., Watts, S.E.: Multiscale topology optimization using neural network surrogate models. Comput. Methods Appl. Mech. Eng. 346, 1118–1135 (2019)

    MathSciNet  Google Scholar 

  24. Groen, J.P., Wu, J., Sigmund, O.: Homogenization-based stiffness optimization and projection of 2D coated structures with orthotropic infill. Comput. Methods Appl. Mech. Eng. 349, 722–742 (2019)

    MathSciNet  Google Scholar 

  25. Bessa, M., Bostanabad, R., Liu, Z., Hu, A., Apley, D.W., Brinson, C., Chen, W., Liu, W.K.: A framework for data-driven analysis of materials under uncertainty: countering the curse of dimensionality. Comput. Methods Appl. Mech. Eng. 320, 633–667 (2017)

    MathSciNet  Google Scholar 

  26. Liu, Z., Fleming, M., Liu, W.K.: Microstructural material database for self-consistent clustering analysis of elastoplastic strain softening materials. Comput. Methods Appl. Mech. Eng. 330, 547–577 (2018)

    MathSciNet  Google Scholar 

  27. Xia, L., Breitkopf, P.: Multiscale structural topology optimization with an approximate constitutive model for local material microstructure. Comput. Methods Appl. Mech. Eng. 286, 147–167 (2015)

    MathSciNet  Google Scholar 

  28. Zhu, L., Li, M., Xu, W.: Direct design to stress mapping for cellular structures. Visual Inf. 3(2), 69–80 (2019)

    Google Scholar 

  29. Groen, J.P., Sigmund, O.: Homogenization-based topology optimization for high-resolution manufacturable microstructures: homogenization-based topology optimization for high-resolution manufacturable microstructures. Int. J. Numer. Meth. Eng. 113(8), 1148–1163 (2018)

    Google Scholar 

  30. Wu, J., Wang, W., Gao, X.: Design and optimization of conforming lattice structures. IEEE Trans. Visual Comput. Graph. 27(1), 43–56 (2019)

    Google Scholar 

  31. Holdstein, Y., Fischer, A.: Three-dimensional surface reconstruction using meshing growing neural gas (MGNG). Vis. Comput. 24, 295–302 (2008)

    Google Scholar 

  32. Lefik, M., Boso, D.P., Schrefler, B.A.: Artificial neural networks in numerical modelling of composites. Comput. Methods Appl. Mech. Eng. 198(21), 1785–1804 (2009)

    Google Scholar 

  33. Le, B.A., Yvonnet, J., He, Q.-C.: Computational homogenization of nonlinear elastic materials using neural networks: neural networks-based computational homogenization. Int. J. Numer. Meth. Eng. 104(12), 1061–1084 (2015)

    Google Scholar 

  34. Liu, Z., Wu, C., Koishi, M.: A deep material network for multiscale topology learning and accelerated nonlinear modeling of heterogeneous materials. Comput. Methods Appl. Mech. Eng. 345, 1138–1168 (2019)

    MathSciNet  Google Scholar 

  35. Yang, X., Li, M., Zhu, L., Zhong, W.: Evolutionary discrete multi-material topology optimization using CNN-based simulation without labeled training data, in: International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Vol. 85376, American Society of Mechanical Engineers, p. V002T02A027, (2021)

  36. Peng, H., Liu, A., Huang, J., Cao, L., Liu, J., Lu, L.: Ph-net: parallelepiped microstructure homogenization via 3d convolutional neural networks. Addit. Manufact. 60, 103237 (2022)

    Google Scholar 

  37. Ronneberger O., Fischer, P., Brox, T.: U-net: Convolutional networks for biomedical image segmentation (2015). arXiv:1505.04597

  38. Papanicolau, G., Bensoussan, A., Lions, J.-L.: Asymptotic analysis for periodic structures, vol. 5. Elsevier, UK (1978)

    Google Scholar 

  39. Palencia, E.S.: Non-homogeneous media and vibration theory. Springer-Verlag, USA (1980)

    Google Scholar 

  40. Bendsøe, M.P., Kikuchi, N.: Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 71(2), 197–224 (1988)

    MathSciNet  Google Scholar 

  41. Beck, C., Becker, S., Grohs, P., Jaafari, N., Jentzen, A.: Solving stochastic differential equations and Kolmogorov equations by means of deep learning, arXiv:1806.00421 (2018)

  42. Berg, J., Nyström, K.: A unified deep artificial neural network approach to partial differential equations in complex geometries. Neurocomputing 317, 28–41 (2018)

    Google Scholar 

  43. Zhu, Y., Zabaras, N., Koutsourelakis, P.-S., Perdikaris, P.: Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. J. Comput. Phys. 394, 56–81 (2019)

    MathSciNet  Google Scholar 

  44. Sigmund, O.: Materials with prescribed constitutive parameters: an inverse homogenization problem. Int. J. Solids Struct. 31(17), 2313–2329 (1994)

    MathSciNet  Google Scholar 

  45. Gu, J., Wang, Z., Kuen, J., Ma, L., Shahroudy, A., Shuai, B., Liu, T., Wang, X., Wang, G., Cai, J., et al.: Recent advances in convolutional neural networks. Pattern Recogn. 77, 354–377 (2018)

    Google Scholar 

  46. Garg, R., BG, V.K., Carneiro, G., Reid, I.: Unsupervised CNN for single view depth estimation: geometry to the rescue, in: European Conference on Computer Vision, Springer, 2016, pp. 740–756

  47. Zhang, Y., Chan, W., Jaitly, N.: Very deep convolutional networks for end-to-end speech recognition, in: 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), IEEE, pp. 4845–4849, (2017)

  48. Simonyan, K., Zisserman, A.: Very deep convolutional networks for large-scale image recognition, arXiv preprint arXiv:1409.1556 (2014)

  49. Andreassen, E., Andreasen, C.S.: How to determine composite material properties using numerical homogenization. Comput. Mater. Sci. 83, 488–495 (2014)

    Google Scholar 

  50. Dong, G., Tang, Y., Zhao, Y.F.: A 149 line homogenization code for three-dimensional cellular materials written in MATLAB. J. Eng. Mater. Technol. 141(1), 011005 (2019)

    Google Scholar 

  51. Cheng, L., Zhang, P., Biyikli, E., Bai, J., Pilz, S.: To, A.C. Integration of topology optimization with efficient design of additive manufactured cellular structures, in: Solid Freeform Fabrication Symposium, Austin, TX, pp. 10–12, (2015)

  52. Yoo, D.-J.: Computer-aided porous scaffold design for tissue engineering using triply periodic minimal surfaces. Int. J. Precis. Eng. Manuf. 12(1), 61–71 (2011)

  53. Yang, N., Quan, Z., Zhang, D., Tian, Y.: Multi-morphology transition hybridization CAD design of minimal surface porous structures for use in tissue engineering. Comput. Aided Des. 56, 11–21 (2014)

  54. Dong, L., Gamal, S.H., Atluri, S.N.: Stochastic macro material properties, through direct stochastic modeling of heterogeneous microstructures with randomness of constituent properties and topologies, by using trefftz computational grains (tcg), CMC: Computers. Materials & Continua 37(1), 1–21 (2013)

    Google Scholar 

  55. Smith, L.N.: A disciplined approach to neural network hyper-parameters: part 1–learning rate, batch size, momentum, and weight decay, arXiv preprint arXiv:1803.09820 (2018)

Download references

Acknowledgements

We would like to thank all the anonymous reviewers for their valuable comments and suggestions. The work described in this paper is partially supported by the National Key Research and Development Program of China (No. 2020YFC2201303), and the NSF of China (No. 62372401).

Author information

Authors and Affiliations

  1. State Key Laboratory of CAD & CG, Zhejiang University, Hangzhou, 310027, China

    Liangchao Zhu, Xuwei Wang, Weidong Zhong & Ming Li

Authors
  1. Liangchao Zhu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xuwei Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Weidong Zhong
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Ming Li
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ming Li.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhu, L., Wang, X., Zhong, W. et al. Learning microstructure–property mapping via label-free 3D convolutional neural network. Vis Comput 40, 7025–7044 (2024). https://doi.org/10.1007/s00371-024-03411-5

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00371-024-03411-5

Keywords