Abstract
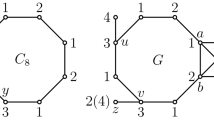
Let G be a graph and A an Abelian group. Denote by F(G, A) the set of all functions from E(G) to A. Denote by D an orientation of E(G). For f ∈ F(G,A), an (A,f)-coloring of G under the orientation D is a function c : V(G)↦A such that for every directed edge uv from u to v, c(u)−c(v) ≠ f(uv). G is A-colorable under the orientation D if for any function f ∈ F(G, A), G has an (A, f)-coloring. It is known that A-colorability is independent of the choice of the orientation. The group chromatic number of a graph G is defined to be the least positive integer m for which G is A-colorable for any Abelian group A of order ≥m, and is denoted by χ g (G). In this note we will prove the following results. (1) Let H 1 and H 2 be two subgraphs of G such that V(H 1)∩V(H 2)=∅ and V(H 1)∪V(H 2)=V(G). Then χ g (G)≤min{max{χ g (H 1), max v ∈ V(H 2) deg(v,G)+1},max{χ g (H 2), max u ∈ V(H 1) deg (u, G) + 1}}. We also show that this bound is best possible. (2) If G is a simple graph without a K 3,3-minor, then χ g (G)≤5.
Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
Bondy, J.A., Murty, U.S.R.: Graph theory with applications, American Elsevier, New York, 1976
Brooks, R.L.: On coloring the nodes of a network. Proc. Cambridge Phil. Soc. 37, 194–197 (1941)
Harary, F.: Graph Theory, Addison-Wesley, 1969
Jaeger, F., Linial, N., Payan, C., Tarsi, M.: Graph connectivity of graphs–a nonhomogeneous analogue of nowhere-zero flow properties. J. Combin. Theory, B. 56, 165–182 (1992)
Kuratowski, K.: Sur la problème des courbes gauches en topologie. Fund. Math. 156, 271–283 (1930)
Lai, H.-J., Zhang, X.: Group colorability of graphs. Ars Combinatorics 62, 299–317 (2002)
Lai, H.-J., Zhang, X.: Group chromatic number of graphs without K 5-minors. Graphs and Combinatorics 18, 147–154 (2002)
Wagner, K.: Über eine eigneschaft der ebenen komplexe. Math. Ann. 144, 570–590 (1937)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Lai, HJ., Li, X. On Group Chromatic Number of Graphs. Graphs and Combinatorics 21, 469–474 (2005). https://doi.org/10.1007/s00373-005-0625-0
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/s00373-005-0625-0