Abstract
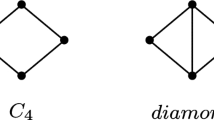
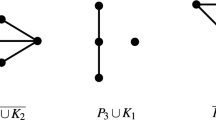
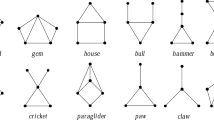
For an arbitrary class of graphs \(\mathcal{G}\), there may not exist a function f such that \(\chi(G) \leq f(\omega(G))\), for every \(G \in \mathcal{G}\). When such a function exists, it is called a χ-binding function for \(\mathcal{G}\). The problem of finding an optimal χ-binding function for the class of 3K 1-free graphs is open. In this paper, we obtain linear χ-binding function for the class of {3K 1, H}-free graphs, where H is one of the following graphs: \(K_1 + C_4, (K_3 \cup K_1)+K_1, K_1 + P_4, K_4 \cup K_1\), House graph and Kite graph. We first describe structures of these graphs and then derive χ-binding functions.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Brown, J.I., Corneil, D.G.: Perfect colorings. Ars Combinatoria 30, 141–159 (1990)
Bondy, J.A., Murty, U.S.R.: Graph theory and its applications. The Macmillan Press Ltd., London (1976)
Choudum, S.A., Shalu, M.A.: The class of {3K 1, C 4}-free graphs. Australasian Journal of Combinatorics 32, 111–116 (2005)
Choudum, S.A., Karthick, T., Shalu, M.A.: Perfect colouring and linearly χ-bound P 6-free graphs. Journal of Graph Theory 54(4), 293–306 (2007)
Chudnovsky, M.: Berge trigraphs. Journal of Graph Theory 53(1), 1–55 (2006)
Chudnovsky, M., Seymour, P.: Claw-free graphs VII. Colouring claw-free graphs. Manuscript (2004)
Chudnovsky, M., Seymour, P., Robertson, N., Thomas, R.: The strong perfect graph theorem. Annals of Mathematics 164(1), 51–229 (2006)
Dhurandhar, M.: On the chromatic number of a graph with two forbidden subgraphs. Journal of Combinatorial Theory, Series B 46, 1–6 (1989)
Fouquet, J.L., Giakoumakis, V., Maire, F., Thuillier, H.: On graphs without P 5 and \(\overline{P_5}\). Discrete Mathematics 146, 33–44 (1995)
Gyárfás, A.: Problems from the world surrounding perfect graphs. Zastosowania Matematyki Applicationes Mathematicae 19, 413–441 (1987)
Hoang, C. T., McDiarmid, C.: On the divisibility of graphs. Discrete Mathematics 242, 145–156 (2002)
Kierstead, H.: On the chromatic index of multigraphs without large triangles. Journal of Combinatorial Theory, Series B 36, 156–160 (1984)
Kim, J. H.: The Ramsey number R(3, t) has order of magnitude t 2/log t. Random Structures and Algorithms 7, 173–207 (1995)
Lovász, L.: A characterization of perfect graphs. Journal of Combinatorial Theory, Series B 13, 95–98 (1972)
Randerath, B., Schiermeyer, I.: Vertex colouring and forbidden subgraphs - A survey. Graphs and Combinatorics 20, 1–40 (2004)
West, D.B.: Introduction to Graph Theory, Second Edition, Prentice-Hall, Englewood Cliffs, New Jersey (2000)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Choudum, S.A., Karthick, T. & Shalu, M.A. Linear Chromatic Bounds for a Subfamily of 3K 1-free Graphs. Graphs and Combinatorics 24, 413–428 (2008). https://doi.org/10.1007/s00373-008-0801-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00373-008-0801-0