An Anti-Ramsey Theorem on Diamonds

Abstract

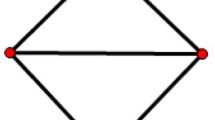
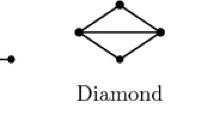
Let G be the diamond (the graph obtained from K ₄ by deleting an edge) and, for every n ≥ 4, let f(n, G) be the minimum integer k such that, for every edge-coloring of the complete graph of order n which uses exactly k colors, there is at least one copy of G all whose edges have different colors. Let ext(n, {C ₃, C ₄}) be the maximum number of edges of a graph on n vertices free of triangles and squares. Here we prove that for every n ≥ 4,

$${\rm {ext}}(n, \{C_3, C_4\})+ 2\leq f(n,G)\leq {\rm {ext}}(n, \{C_3,C_4\})+ (n+1).$$