The Chvátal–Erdös Condition for Group Connectivity in Graphs

Abstract

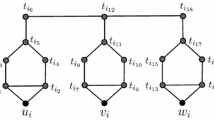
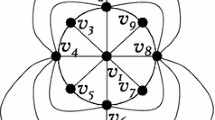
Let G be a graph and A an abelian group with the identity element 0 and ${|A| \geq 4}$ . Let D be an orientation of G. The boundary of a function ${f: E(G) \rightarrow A}$ is the function ${\partial f: V(G) \rightarrow A}$ given by ${\partial f(v) = \sum_{e \in E^+(v)}f(e) - \sum_{e \in E^-(v)}f(e)}$ , where ${v \in V(G), E^+(v)}$ is the set of edges with tail at v and ${E^-(v)}$ is the set of edges with head at v. A graph G is A-connected if for every b: V(G) → A with ${\sum_{v \in V(G)} b(v) = 0}$ , there is a function ${f: E(G) \mapsto A-\{0\}}$ such that ${\partial f = b}$ . A graph G is A-reduced to G′ if G′ can be obtained from G by contracting A-connected subgraphs until no such subgraph left. Denote by ${\kappa^{\prime}(G)}$ and α(G) the edge connectivity and the independent number of G, respectively. In this paper, we prove that for a 2-edge-connected simple graph G, if ${\kappa^{\prime}(G) \geq \alpha(G)-1}$ , then G is A-connected or G can be A-reduced to one of the five specified graphs or G is one of the 13 specified graphs.