Extremal Bicyclic 3-Chromatic Graphs

Abstract

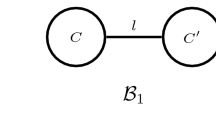
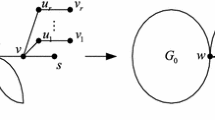
A partial order relation in the set $\mathcal {G}(n,k)$ of graphs of order $n$ and chromatic number $k$ can be defined as follows: Let $G$ and $H$ be two graphs in $\mathcal {G}(n,k)$. $G$ is said to be less than $H$ if $c_i(G)\le c_i(H)$ holds for every $i$, $k\le i\le n$ and at least one inequality is strict, where $c_i(G)$ denotes the number of $i$-color partitions of $G$. These numbers are the coefficients of the chromatic polynomial in factorial form. In (J Graph Theory 43:210–222, 2003) the first $\lceil n/2\rceil$ levels of the diagram of the partially ordered set of connected 3-chromatic graphs of order $n$ were described. In this paper the previous work is continued and a description of the $(\lceil n/2\rceil +1)$-st level is given; it contains $n/2+1$ bicyclic graphs for even $n$ and $(n-1)/2$ bicyclic graphs for odd $n$. Some consequences concerning ordering chromatic polynomials of these graphs are deduced.