Abstract
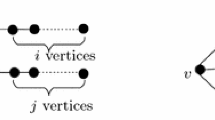
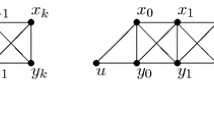
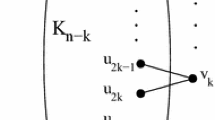
In this paper, we characterize connected \(\{K_{1,3},N(2,1,0)\}\)-free but not \(N(1,1,1)\)-free graphs. By combining our result and a theorem showed by Duffus et al. (every \(2\)-connected \(\{K_{1,3},N(1,1,1)\}\)-free graph is Hamiltonian), we give an alternative proof of Bedrossian’s theorem (every \(2\)-connected \(\{K_{1,3},N(2,1,0)\}\)-free graph is Hamiltonian).


Similar content being viewed by others
References
Bedrossian, P.: Forbidden subgraph and minimum degree conditions for Hamiltonicity, Ph.D. Thesis. Memphis State University (1991)
Diestel,R.: Graph Theory, Graduate Texts in Mathematics 173, Springer (2010)
Duffus,D., Gould, R.J., Jacobson,M.S., Forbidden subgraphs and the Hamiltonian theme. The theory and applications of graphs, pp. 297–316, Wiley, New York (1981)
Faudree, R.J., Gould, R.J.: Characterizing forbidden pairs for hamiltonian properties. Discrete Math 173, 45–60 (1997)
Shepherd, F.B.: Hamiltonicity in claw-free graphs. J Combin Theory Ser B 53, 173–194 (1991)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Furuya, M., Tsuchiya, S. Claw-Free and \(N(2,1,0)\)-Free Graphs are Almost Net-Free. Graphs and Combinatorics 31, 2201–2205 (2015). https://doi.org/10.1007/s00373-014-1506-1
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00373-014-1506-1