Skip to main content
SpringerLink
Log in

\(N\)-Flips in 4-Connected Even Triangulations on the Sphere

  • Original Paper
  • Published:
Graphs and Combinatorics Aims and scope Submit manuscript

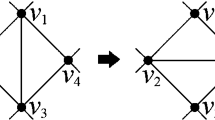
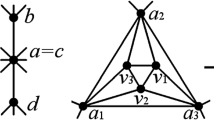
Abstract

An even triangulation is a plane triangulation in which each vertex has even degree. It is well known that every even triangulation \(G\) has a unique 3-coloring, where the decomposition of the vertices of \(G\) by the 3-coloring is called the tripartition of \(G\). Nakamoto et al. (Graph Theory 51:260–268, 2006) proved that every two even triangulations with the same tripartition can be transformed into each other by \(N\)-flips, where an \(N\) -flip is an operation transforming an even triangulation into an even triangulation. In this paper, we prove that every two 4-connected even triangulations \(G\) and \(G'\) with the same tripartition can be transformed into each other by \(N\)-flips unless \(G\) or \(G'\) is isomorphic to a generalized octahedron.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Dewdney, A.K.: Wagner’s theorem for the torus graphs. Discrete Math. 4, 139–149 (1973)

    Article  MathSciNet  MATH  Google Scholar 

  2. Higuchi, Y., Nakamoto, A., Ota, K., Sakuma, T.: \(N\)-flips in even triangulations on the torus and Dehn twists preserving monodromies. Discrete Math. 311, 1128–1135 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  3. Kawarabayashi, K., Nakamoto, A., Suzuki, Y.: \(N\)-flips in even triangulations on surfaces. J. Comb. Theory Ser. B 99, 229–246 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  4. Komuro, H., Nakamoto, A., Negami, S.: Diagonal flips in triangulation on closed surfaces with minimum degree at least 4. J. Comb. Theory Ser. B 76, 68–92 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  5. Matsumoto, N., Nakamoto, A.: Generating 4-connected even triangulations. Discrete Math. 338, 64–70 (2015)

  6. Nakamoto, A.: Diagonal transformations and cycle parites of quadrangulations on surfaces. J. Comb. Theory Ser. B 67, 202–211 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  7. Nakamoto, A.: Diagonal transformations in quadrangulations on surfaces. J. Graph Theory 21, 289–299 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  8. Nakamoto, A.: Quadrangulations on closed surfaces. Interdiscip. Inf. Sci. 7, 77–98 (2001)

    MathSciNet  MATH  Google Scholar 

  9. Nakamoto, A., Sakuma, T., Suzuki, Y.: \(N\)-flips in even triangulation on the sphere. J. Graph Theory 51, 260–268 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  10. Nakamoto, A., Suzuki, Y.: \(N\)-flips in even triangulations on the projective plane. Discrete Math. 308, 5454–5462 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  11. Negami, S.: Diagonal flips in triangulations of surfaces. Discrete Math. 135, 225–232 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  12. Negami, S.: Diagonal flips of triangulations on surfaces, a survey. Yokohama Math. J. 47, 1–40 (1999)

    MathSciNet  MATH  Google Scholar 

  13. Negami, S., Watanabe, T.: Diagonal transformations of triangulations on surfaces. Tsukuba J. Math. 14, 155–166 (1990)

    MathSciNet  MATH  Google Scholar 

  14. Wagner, K.: Bemerkungen zum Vierfarbenproblem. J. der Dtsch. Math. 46, 26–32 (1936)

    Google Scholar 

Download references

Acknowledgments

I am grateful to the two anonymous referees for carefully reading the paper and giving us helpful suggestions to improve the presentation of the paper.

Author information

Authors and Affiliations

  1. Graduate School of Environment and Information Sciences, Yokohama National University, 79-5 Tokiwadai, Hodogaya-ku, Yokohama, 240-8501, Japan

    Yuki Kawasaki & Atsuhiro Nakamoto

  2. Department of Computer and Information Science, Seikei University, 3-3-1 Kichijoji-Kitamachi, Musashino-shi, Tokyo, 180-8633, Japan

    Naoki Matsumoto

Authors
  1. Yuki Kawasaki
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Naoki Matsumoto
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Atsuhiro Nakamoto
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Naoki Matsumoto.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kawasaki, Y., Matsumoto, N. & Nakamoto, A. \(N\)-Flips in 4-Connected Even Triangulations on the Sphere. Graphs and Combinatorics 31, 1889–1904 (2015). https://doi.org/10.1007/s00373-015-1574-x

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00373-015-1574-x

Keywords

Search

Navigation