Richardson’s Theorem in H-coloured Digraphs

Abstract

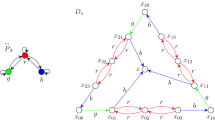
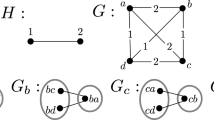
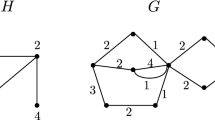
Let H be a digraph possibly with loops and D a finite digraph without loops whose arcs are coloured with the vertices of H (D is an H-coloured digraph). The sets V(D) and A(D) will denote the sets of vertices and arcs of D respectively. A directed path W in D is an H-path if and only if the consecutive colors encountered on W form a directed walk in H. A set $N\subseteq \hbox {V}(D)$ is an H-kernel if for every pair of different vertices in N there is no H-path between them, and for every vertex $u\in \hbox {V}(D){\setminus }N$ there exists an H-path in D from u to N. Let D be an m-coloured digraph. The color-class digraph of D, denoted by ${\mathscr {C}}_C(D$), is the digraph such that: the vertices of the color-class digraph are the colors represented in the arcs of D, and $(i,j) \in A({\mathscr {C}}_C(D$)) if and only if there exist two arcs namely (u, v) and (v, w) in D such that (u, v) has color i and (v, w) has color j. Let $W=(v_0, \ldots , v_n$) be a directed walk in ${\mathscr {C}}_C(D)$, with D an H-coloured digraph, and $e_i = (v_{i},v_{i+1})$ for each $i \in \{0, \ldots ,n-1\}$. Let $I = \{i_1, \ldots , i_k\}$ a subset of $\{0, \ldots , n-1\}$ such that for 0 $\le s \le n-1$, $e_s \in \hbox { A}(H^c)$ if and only if $s \in I$ (where $H^c$ is the complement of H), then we will say that k is the $H^c$-length of W. Since V(${\mathscr {C}}_C(D)) \subseteq \hbox {V}(H)$, the main question is: What structural properties of ${\mathscr {C}}_C(D)$, with respect to H, imply that D has an H-kernel? In this paper we will prove the following: If ${\mathscr {C}}_C(D)$ does not have directed cycles of odd $H^c$-length, then D has an H-kernel. Finally we will prove Richardson’s theorem as a direct consequence of the previous result.