Skip to main content
Springer Nature Link
Log in

Hamilton Cycles in Implicit 2-Heavy Graphs

  • Original Paper
  • Published:
Graphs and Combinatorics Aims and scope Submit manuscript

Abstract

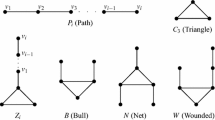
Let id(v) denote the implicit degree of a vertex v in a graph G. We define G of order n to be implicit 2-heavy if at least two of the end vertices of each induced claw have implicit degree at least \(\frac{n}{2}\). In this paper, we show that every implicit 2-heavy graph G is hamiltonian if we impose certain additional conditions on the connectivity of G or forbidden induced subgraphs. Our results extend two previous theorems of Broersma et al. (Discret Math 167–168:155–166, 1997) on the existence of Hamilton cycles in 2-heavy graphs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Bondy, J.A.: Large cycles in graphs. Discret. Math. 1, 121–132 (1971)

    Article  MathSciNet  MATH  Google Scholar 

  2. Bondy, J.A.: Longest paths and cycles in graphs of high degree. In: Research Report CORR 80-16. Univ. of Waterloo, Waterloo (1980)

  3. Bondy, J.A., Murty, U.S.R.: Graph Theory with Applications. Macmillan, London (1976)

    Book  MATH  Google Scholar 

  4. Broersma, H.J., Ryjáček, Z., Schiermeyer, I.: Dirac’s minimum degree condition restricted to claws. Discret. Math. 167–168, 155–166 (1997)

    Article  MATH  Google Scholar 

  5. Broersma, H.J., Veldman, H.J.: Restrictions on induced subgaphs ensuring hamiltonicity or pancyclicity of \(K_{1,3}\)-free graphs. In: Bodendiek, R. (ed.) Contemporary Methods in Graph Theory, pp. 181–194. BI-Wiss.-Verl., Mannhein (1990)

    Google Scholar 

  6. Faudree, R.J., Ryjáček, Z., Schiermeyer, I.: Forbidden subgraphs and cycle extendability. J. Comb. Math. Comb. Comput. 19, 109–128 (1995)

    MathSciNet  MATH  Google Scholar 

  7. Li, H., Ning, W.T., Cai, J.Q.: An implicit degree condition for cyclability in graphs, FAW-AAIM 2011. LNCS 6681, 82–89 (2011)

    MATH  Google Scholar 

  8. Oberly, D.J., Sumner, D.P.: Every connected, locally connected nontrivial graph with no induced claw is hamiltonian. J. Graph Theory 3, 351–356 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  9. Yamashita, T.: On degree sum conditions for long cycles and cycles through specified vertices. Discret. Math. 308, 6584–6587 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  10. Zhu, Y., Li, H., Deng, X.: Implicit-degrees and circumferences. Gr. Comb. 5, 283–290 (1989)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The authors are very grateful to the anonymous referee whose helpful comments and suggestions have led to a substantially improvement of the paper.

Author information

Authors and Affiliations

  1. School of Management, Qufu Normal University, Rizhao, 276826, People’s Republic of China

    Junqing Cai

  2. L.R.I, UMR 8623, CNRS, Université Paris-Sud 11, 91405, Orsay, France

    Hao Li

  3. Institute for Interdisciplinary Research, Jianghan University, Wuhan, 430019, People’s Republic of China

    Hao Li

Authors
  1. Junqing Cai
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hao Li
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Junqing Cai.

Additional information

This work is supported by Postdoctoral Science Foundation of China (No. 2015M571999), National Natural Science Foundation of China (Nos. 11501322, 11426145), Natural Science Foundation of Shandong Province (No. ZR2014AP002) and Scientific Research Foundation for Doctors in Qufu Normal University (No. 2012015).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cai, J., Li, H. Hamilton Cycles in Implicit 2-Heavy Graphs. Graphs and Combinatorics 32, 1329–1337 (2016). https://doi.org/10.1007/s00373-015-1669-4

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00373-015-1669-4

Keywords