Dominating Cycles and Forbidden Pairs Containing $P_{5}$

Abstract

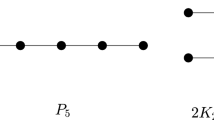
A cycle C in a graph G is dominating if every edge of G is incident with at least one vertex of C. For a set $\mathcal {H}$ of connected graphs, a graph G is said to be $\mathcal {H}$-free if G does not contain any member of $\mathcal {H}$ as an induced subgraph. When $|\mathcal {H}| = 2, \mathcal {H}$ is called a forbidden pair. In this paper, we investigate the characterization of the class of the forbidden pairs guaranteeing the existence of a dominating cycle and show the following two results: (i) Every 2-connected $\{P_{5}, K_{4}^{-}\}$-free graph contains a longest cycle which is a dominating cycle. (ii) Every 2-connected $\{P_{5}, W^{*}\}$-free graph contains a longest cycle which is a dominating cycle. Here $P_{5}$ is the path of order $5, K_{4}^{-}$ is the graph obtained from the complete graph of order 4 by removing one edge, and $W^{*}$ is the graph obtained from two triangles and an edge by identifying one vertex in each.