Skip to main content
Springer Nature Link
Log in

Forbidden Pairs for Equality of Connectivity and Edge-Connectivity of Graphs

  • Original Paper
  • Published:
Graphs and Combinatorics Aims and scope Submit manuscript

Abstract

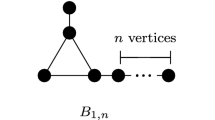
Let \({\mathcal {H}}\) be a set of connected graphs. A graph is said to be \({\mathcal {H}}\)-free if it does not contain any member of \({\mathcal {H}}\) as an induced subgraph. In this paper, we characterize all pairs R, S such that every connected \(\{R,S\}\)-free graph has the same (vertex)-connectivity and edge-connectivity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Bedrossian, P.: Forbidden subgraph and minimum degree conditions for Hamiltonicity (Ph.D. thesis), Memphis State University (1991)

  2. Bondy, J.A., Murty, U.S.R.: Graph Theory, Graduate in Mathematics, vol. 244. Springer, New York (2008)

    Book  Google Scholar 

  3. Chiba, S., Furuya, M., Tsuchiya, S.: Forbidden pairs and the existence of a dominating cycle. Discrete Math. 338, 2442–2452 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  4. Faudree, R.J., Gould, R.J.: Characterizing forbidden pairs for Hamiltonian properties. Discrete Math. 173, 45–60 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  5. Fujita, S., Kawarabayashi, K., Lucchesi, C., Ota, K., Plummer, M., Saito, A.: A pair of forbidden subgraphs and perfect matchings. J. Comb. Theory Ser. B 96, 315–324 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  6. Ryjáček, Z., Vrána, P., Xiong, L.: Hamiltonian properties of 3-connected {claw, hourglass}-free graphs. Discrete Math. 341, 1806–1815 (2018)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The first author is funded by International Graduate Exchange Program of Beijing Institute of Technology. The second author is partially supported by JSPS KAKENHI Grant number JP16K17646. The third author is supported by the Natural Science Funds of China (Nos: 11871099, 11671037).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Beijing Institute of Technology, Beijing, 100081, People’s Republic of China

    Shipeng Wang

  2. School of Network and Information, Senshu University, 2-1-1 Higashimita, Tama-ku, Kawasaki, Kanagawa, 214-8580, Japan

    Shoichi Tsuchiya

  3. School of Mathematics and Statistics, Beijing Key Laboratory on MCAACI, Beijing Institute of Technology, Beijing, 100081, People’s Republic of China

    Liming Xiong

Authors
  1. Shipeng Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Shoichi Tsuchiya
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Liming Xiong
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Liming Xiong.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, S., Tsuchiya, S. & Xiong, L. Forbidden Pairs for Equality of Connectivity and Edge-Connectivity of Graphs. Graphs and Combinatorics 35, 419–426 (2019). https://doi.org/10.1007/s00373-018-2003-8

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00373-018-2003-8

Keywords