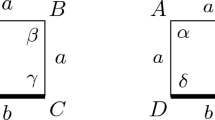Skip to main content
SpringerLink
Log in

Rhombus Tilings of an Even-Sided Polygon and Quadrangulations on the Projective Plane

  • Original Paper
  • Published:
Graphs and Combinatorics Aims and scope Submit manuscript

Abstract

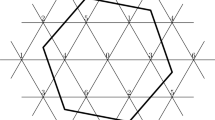
A quadrangulation on a closed surface is k-minimal if its shortest noncontractible cycle is of length k and if any face contraction yields a noncontractible cycle of length less than k. We prove that the rhombus tilings of a regular 2k-gon bijectively correspond to the pairs of a k-minimal quadrangulations on the projective plane and its specified noncontractible k-cycle.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Bohne, J.: Eine kombinatorische Analyze zonotopaler Raumaufteilungen, Dissertation, Bielefeld 1992; Preprint 92-041, SFB 343, Universität Bielefeld , 100 pages (1992)

  2. Elnitsky, S.: Rhombic tilings of polygons and classes of reduced words in Coxeter groups. J. Combin. Theory Ser. A 77, 193–221 (1997)

    Article  MathSciNet  Google Scholar 

  3. Eppstein, D.: Zonohedra and zonotopes. Math. Educ. Res. 5, 15–21 (1996)

    Google Scholar 

  4. Kaiser, T., Stehlík, M.: Colouring quadrangulations of projective spaces. J. Combin. Theory Ser. B 113, 1–17 (2013)

    Article  MathSciNet  Google Scholar 

  5. Kenyon, R.: Tiling a polygon with parallelograms. Algorithmica 9, 382–397 (1993)

    Article  MathSciNet  Google Scholar 

  6. Nakamoto, A.: Irreducible quadrangulations of the torus. J. Combin. Theory Ser. B 67, 183–201 (1996)

    Article  MathSciNet  Google Scholar 

  7. Nakamoto, A.: Irreducible quadrangulations of the Klein bottle. Yokohama Math. J. 43, 125–139 (1995)

    MathSciNet  MATH  Google Scholar 

  8. Nakamoto, A., Suzuki, Y.: Y-Rotations in \(k\)-minimal quadrangulations on the projective plane. J. Graph Theory 69, 301–313 (2012)

    Article  MathSciNet  Google Scholar 

  9. Negami, S., Nakamoto, A.: Diagonal transformations of graphs on closed surfaces. Sci. Rep. Yokohama Nat. Univ. Sect. I Math. Phys. Chem. 40, 71–97 (1993)

    MathSciNet  Google Scholar 

  10. Randby, S.: Minimal embeddings in the projective plane. J. Graph Theory 25, 153–163 (1997)

    Article  MathSciNet  Google Scholar 

  11. Richter-Gebert, J., Ziegler, G.M.: Zonotopal tilings and the Bohne-Dress theorem. Amer. Math. Soc. Contemp. Math. 178, 211–232 (1994)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

We are grateful to the anonymous referee for his valuable suggestion to introduce the notion of zonotopes. Using this notion, we have been able to explain our inductive proof of the results very naturally, and consider a possible extension of our result to 3-dimensional objects. These improvements along them has greatly enhanced the readability of the paper.

Funding

This research was supported by Japan Society for the Promotion of Science (KAKENHI Grant Number 18K03390).

Author information

Authors and Affiliations

  1. Department of Mathematics and Natural Sciences, Hyogo University of Teacher Education, 942-1 Shimokume, Kato, Hyogo, 673-1494, Japan

    Hiroaki Hamanaka

  2. Faculty of Environment and Information Sciences, Yokohama National University, 79-2 Tokiwadai, Hodogaya-Ku, Yokohama, 240-8501, Japan

    Atsuhiro Nakamoto

  3. Department of Mathematics, Niigata University, 8050 Ikarashi 2-no-cho, Nishi-Ku, Niigata, 950-2181, Japan

    Yusuke Suzuki

Authors
  1. Hiroaki Hamanaka
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Atsuhiro Nakamoto
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yusuke Suzuki
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Atsuhiro Nakamoto.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hamanaka, H., Nakamoto, A. & Suzuki, Y. Rhombus Tilings of an Even-Sided Polygon and Quadrangulations on the Projective Plane. Graphs and Combinatorics 36, 561–571 (2020). https://doi.org/10.1007/s00373-020-02137-0

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00373-020-02137-0

Keywords

Mathematics Subject Classification

Search

Navigation