H-Cycles in H-Colored Multigraphs

Abstract

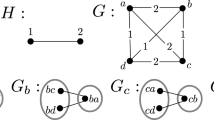
Let H be a graph possibly with loops and G a multigraph without loops. G is said to be H-colored if there exists a function c: E(G) $\rightarrow$ V(H). A cycle ($v_0$, $e_0$, $v_1$, $e_1$, $\ldots$ , $e_{k-1}$, $v_k = v_0$) in G, where $e_i = v_iv_{i+1}$ for every i in {0, $\ldots$ , $k-1$}, is an H-cycle if and only if (c($e_0$), $a_0$, c($e_1$), $\ldots$ , c($e_{k-2}$), $a_{k-2}$, c($e_{k-1}$), $a_{k-1}$, c($e_0$)) is a walk in H, with $a_i$ = c($e_{i}$)c($e_{i+1}$) for every i in {0, $\ldots$ , $k-1$} (indices modulo k). If H is a complete graph without loops, an H-walk is called properly colored walk. The problem of check whether an edge-colored graph G contains a properly colored cycle was studied first by Grossman and Häggkvist. Subsequently Yeo gave a sufficient condition which guarantee the existence of a properly colored cycle. In this paper we will extend Yeo’s result for the case where stronger requirements are enforced for a properly colored cycle to be eligible, based on the adjacencies of a graph whose vertices are in bijection with the colors. The main result establishes that if H is a graph without loops and G is an H-colored multigraph such that (1) H and G have no isolated vertices, (2) G has no H-cycles and (3) for every x in V(G), $G_x$ is a complete $k_x$-partite graph for some $k_x$ in ${\mathbb {N}}$. Then there exists a vertex z in V(G) such that every connected component D of $G-z$ satisfies that {e $\in$ E(G) : $e=zu$ for some u in V(D)} is an independent set in $G_z$ (where for w in V(G), $G_w$ is an associated graph to the vertex w, respect to the H-coloring of G).