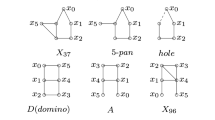
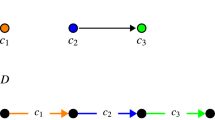
Abstract
Let \(D=(V,E)\) and \(H=(U,F)\) be digraphs and consider a colouring of the arcs of D with the vertices of H; we say that D is H coloured. We study a natural generalisation of the notion of kernel, as introduced by V. Neumann and Morgenstern (1944), to prove that If every cycle of D is an H-cycle, then D has an H-kernel by walks. As a consequence of this, we are able to give several sufficient conditions for the existence of H-kernels by walks; in particular, we solve partially a conjecture by Bai et al. in this context [2]; viz., they work with complete H without loops, and use paths rather than walks, so whenever the existence of H-paths is implied by the existence of H-walks our result can be use to corroborate Bai’s conjecture—in particular, if D is two coloured, and each cycle is alternating, then each alternating walk contains an alternating path.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Arpin, P., Linek, V.: Reachability problems in edge colored digraphs. Discret. Math. 307, 2276–2289 (2007)
Bai, Y., Fujita, Sh., Zhang, Sh.: Kernels by properly colored paths in arc-colored digraphs. Discret. Math. 341, 1523–1533 (2018)
Bang-Jensen, J., Gutin, G.: Digraphs: Theory, Algorithms and Applications. Springer, London (2009)
Duchet, P.: Graphes noyau parfaits. Ann. Discret. Math. 9, 93–101 (1980)
Fraenkel, A.S.: Planar kernel and Grundy width \(d\le 3, d_{out}\le 2, d_{in}\le 2\), are NP-complete. Discret. Appl. Math. 3, 257–262 (1981)
Galeana, H., Montellano, J.J.: A Richardson?s theorem version for \(\Pi \)-kernels. Discret. Math. 340, 984–987 (2017)
Galeana, H., Strausz, R.: On panchromatic patterns. Discret. Math. 339, 2536–2542 (2016)
Linek, V., Sans, B.: A note on paths in edge colored tournaments. Ars Combin. 44, 225–228 (1996)
Von Neumann, J., Morgenstern, O.: Theory of Games and Economic Behavior. Princeton University Press, Princeton (1944)
Richardson, M.: Extension theorems for solutions of irreflexive relations. Proc. Natl. Acad. Sci. U.S.A. 39, 649 (1953)
Sands, B., Sauer, N., Woodrow, R.: On monochromatic paths in edge coloured digraphs. J. Combin. Theory B 33, 271–275 (1982)
Chvátal, V.: On the computational complexity of finding a kernel. Reports CRM 300, Centre de Recherches Matematiques, Universite de Montreal (1973)
Funding
The authors have not disclosed any funding.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors have not disclosed any competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Galeana-Sánchez, H., Rincon-Galeana, H. & Strausz, R. H-Kernels by Walks. Graphs and Combinatorics 38, 94 (2022). https://doi.org/10.1007/s00373-022-02469-z
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00373-022-02469-z