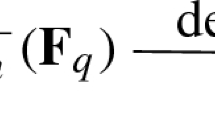Equivariant Euler Characteristics of Symplectic Buildings

Abstract

We compute the equivariant Euler characteristics of the buildings for the symplectic groups over finite fields.

Appendices

Appendix A. Equivariant Euler Characteristics of Posets

This appendix contains a few elementary observations about equivariant Euler characteristics for group actions on posets.

Let S be a finite set and $\dim :S \rightarrow \mathbf {Z}$ a function associating an integer $\ge -1$ to every element of S. The Euler characteristic and the reduced Euler characteristic of the graded set $(S,\dim )$ are the alternating sums

$$\begin{aligned} &\chi (S,\dim )= {} \sum _{d \ge 0} (-1)^d|\dim ^{-1}(d)| \\ & {\tilde{\upchi}} (S,\dim )= \sum _{d \ge -1} (-1)^d|\dim ^{-1}(d)| = \chi (S,\dim )-|\dim ^{-1}(-1)| \end{aligned}$$

of the numbers of d-dimensional elements of S for $d \ge 0$ or $d \ge -1$.

Let $\Pi$ be a finite poset. A simplex in $\Pi$ is a totally ordered subset of $\Pi$. The set $|\Pi |$ of all simplices in $\Pi$ (including the empty simplex) is graded by the function $\dim :|\Pi | \rightarrow \mathbf {Z}$ taking a simplex $\sigma \subseteq \Pi$ to one less than its cardinality, $\dim \sigma = |\sigma |-1$.

Definition A.1

The Euler characteristic of the poset $\Pi$ is $\chi (\Pi ) = \chi (|\Pi |,\dim )$ and the reduced Euler characteristic is ${\tilde{\upchi}} (\Pi ) = {\tilde{\upchi}} (|\Pi |,\dim ) =\chi (\Pi )-1$.

Let G be a finite group. Write ${\text {Hom}}_{}(\mathbf {Z}^r,G)$ for the set of homomorphisms of $\mathbf {Z}^r$ to G and ${\text {Hom}}_{}(\mathbf {Z}^r,G)/G$ for the set of conjugacy classes of such homomorphisms. Equivalently, ${\text {Hom}}_{}(\mathbf {Z}^r,G)$ is the set of commuting r-tuples of elements in G and ${\text {Hom}}_{}(\mathbf {Z}^r,G)/G$ is the set of conjugacy classes of commuting r-tuples.

Suppose now that G acts on the poset $\Pi$ through order preserving bijections. For any subset X of G, let $C_\Pi (X)=\{u \in \Pi \vert \forall g \in X :u^g = u \}$ denote the full subposet of elements of $\Pi$ fixed under the action from X. For any prime number p, let $Z_p^r = \mathbf {Z}\times \mathbf {Z}_p^{r-1}$ where $\mathbf {Z}_p$ is the abelian group of p-adic integers.

Definition A.2

[2, 25] The rth, $r \ge 1$, (p-primary) equivariant Euler characteristic and (p-primary) reduced equivariant Euler characteristic of the G-poset $\Pi$ are

$$\begin{aligned}&\chi _r(\Pi ,G) = \frac{1}{|G|} \sum _ {X \in {\text {Hom}}_{}(\mathbf {Z}^r,G)} \chi (C_\Pi (X(\mathbf {Z}^r)))\\& \chi _r(p,\Pi ,G) = \frac{1}{|G|} \sum _ {X \in {\text {Hom}}_{}(Z_p^r,G)} \chi (C_\Pi (X(Z_p^r))) \\&{\tilde{\upchi}}_r(\Pi ,G) = \frac{1}{|G|} \sum _ {X \in {\text {Hom}}_{}(\mathbf {Z}^r,G)} {\tilde{\upchi}} (C_\Pi (X(\mathbf {Z}^r)))\\& {\tilde{\upchi}}_r(p,\Pi ,G) = \frac{1}{|G|} \sum _ {X \in {\text {Hom}}_{}(Z_p^r,G)}{\tilde{\upchi}} (C_\Pi (X(Z_p^r))) \end{aligned}$$

We note that ${\tilde{\upchi}} _1(p,\Pi ,G)={\tilde{\upchi}} _1(\Pi ,G)$ for all primes p since $Z_p^1 = \mathbf {Z}$. Also, $\chi _r(\Pi ,G) = {\tilde{\upchi}}_r(\Pi ,G) + |{\text {Hom}}_{}(\mathbf {Z}^r,G)|/|G|$ and $\chi _r(p,\Pi ,G) = {\tilde{\upchi}}_r(p,\Pi ,G) + |{\text {Hom}}_{}(Z_p^r,G)|/|G|$. The numbers of conjugacy classes of r-tuples of commuting elements of G and commuting p-power order elements are

$$\begin{aligned} |{\text {Hom}}_{}(\mathbf {Z}^{r-1},G)/G|= & {} |{\text {Hom}}_{}(\mathbf {Z}^{r},G)|/|G|, \\ |{\text {Hom}}_{}(\mathbf {Z}_p^{r-1},G)/G|= & {} |{\text {Hom}}_{}(Z_p^{r},G)|/|G| \qquad (r \ge 1) \end{aligned}$$

as $|{\text {Hom}}_{}(K,G)/G| = |{\text {Hom}}_{}(\mathbf {Z}\times K,G)|/|G|$ for any group K [10, Lemma 4.13].

The equivariant Euler characteristics satisfy a recurrence relation.

Lemma A.3

For all $r \ge 1$,

$$\begin{aligned}{\tilde{\upchi}}_{r+1}(\Pi ,G) & = \sum _{X \in {\text {Hom}}_{}(\mathbf {Z},G)/G} {\tilde{\upchi}}_r(C_\Pi (X),C_G(X)) \\&= \sum _{X \in {\text {Hom}}_{}(\mathbf {Z}^r,G)/G} {\tilde{\upchi}}_1(C_\Pi (X),C_G(X)) \\{\tilde{\upchi}}_{r+1}(p,\Pi ,G) &= \sum _{X \in {\text {Hom}}_{}(\mathbf {Z}_p,G)/G} {\tilde{\upchi}}_r(p,C_\Pi (X),C_G(X)) \\&= \sum _{X \in {\text {Hom}}_{}(\mathbf {Z}_p^r,G)/G} {\tilde{\upchi}}_1(C_\Pi (X),C_G(X)) \end{aligned}$$

and similar formulas are true for $\chi _{r+1}(\Pi ,G)$ and $\chi _{r+1}(p,\Pi ,G)$.

Proof

A little more generally, we consider ${\tilde{\upchi}}_{r_1+r_2}(p,\Pi ,G)$ for $r_1 \ge 1$ and $r_2 \ge 2$. The p-primary equivariant Euler characteristic is

$$\begin{aligned}{\tilde{\upchi}}_{r_1+r_2}(p,\Pi ,G) &= \frac{1}{|G|} \sum _{X \in {\text {Hom}}_{}(\mathbf {Z}\times \mathbf {Z}_p^{r_1+r_2-1},G)} {\tilde{\upchi}} (C_\Pi (X))\\&=\frac{1}{|G|} \sum _{X_1 \in {\text {Hom}}_{}(\mathbf {Z}_p^{r_1},G)}\sum _ {X_2 \in {\text {Hom}}_{}(\mathbf {Z}\times \mathbf {Z}^{r_2-1},C_G(X_1))} {\tilde{\upchi}} (C_{C_\Pi (X_1)}(X_2)) \\&= \frac{1}{|G|} \sum _{X_1 \in {\text {Hom}}_{}(\mathbf {Z}_p^{r_1},G)} |C_G(X_1)| {\tilde{\upchi}}_{r_2}(p,C_\Pi (X_1),C_G(X_1))\\& =\sum _{X_1 \in {\text {Hom}}_{}(\mathbf {Z}_p^{r_1},G)/G} {\tilde{\upchi}}_{r_2}(p,C_\Pi (X_1),C_G(X_1)) \end{aligned}$$

where we use that the conjugacy class of $X_1(\mathbf {Z}_p^{r_1})$ contains $|G : C_G(X_1)|$ elements. $\square$

The set $|C_\Pi (X)|/C_G(X)$ of $C_G(X)$-orbits of $C_\Pi (X)$-simplices, for any $X \subseteq G$, has Euler characteristic relative to the dimension function induced by $\dim :|\Pi | \rightarrow \{-1,0,1,\ldots \}$, $\dim \sigma = |\sigma |-1$.

Lemma A.4

For all $r \ge 0$,

$$\begin{aligned} {\tilde{\upchi}}_{r+1}(\Pi ,G)= & {} \sum _{X \in {\text {Hom}}_{}(\mathbf {Z}^{r},G)/G} {\tilde{\upchi}} (|C_\Pi (X)|/C_G(X)), \\ {\tilde{\upchi}}_{r+1}(p,\Pi ,G)= & {} \sum _{X \in {\text {Hom}}_{}(\mathbf {Z}_p^{r},G)/G} {\tilde{\upchi}} (|C_\Pi (X)|/C_G(X)) \end{aligned}$$

Proof

We first consider the case $r=0$. The orbit counting formula shows that

$$\begin{aligned} {\tilde{\upchi}} (|\Pi |/G)&= \sum _{d \ge -1} (-1)^d | \dim ^{-1}(d)/G |\\&=\frac{1}{|G|} \sum _{d \ge -1} (-1)^d \sum _{g \in G} ||C_\Pi (g)| \cap \dim ^{-1}(d)|\\&=\frac{1}{|G|} \sum _{g \in G} \sum _{d \ge -1} (-1)^d ||C_\Pi (g)| \cap \dim ^{-1}(d) |\\&= \frac{1}{|G|}\sum _{g \in G} {\tilde{\upchi}} (C_\Pi (g)) = {\tilde{\upchi}}_1(\Pi ,G) \end{aligned}$$

Consequently, for all $r \ge 1$,

$$\begin{aligned}{\tilde{\upchi}}_{r+1}(\Pi ,G) &= \sum _{X \in {\text {Hom}}_{}(\mathbf {Z}^{r},G)/G} {\tilde{\upchi}}_1(C_\Pi (X),C_G(X)) \\&= \sum _{X \in {\text {Hom}}_{}(\mathbf {Z}^{r},G)/G} {\tilde{\upchi}} (|C_\Pi (X)|/C_G(X)) \\ {\tilde{\upchi}}_{r+1}(p,\Pi ,G) &= \sum _{X \in {\text {Hom}}_{}(\mathbf {Z}_p^{r},G)/G} {\tilde{\upchi}}_1(C_\Pi (X),C_G(X)) \\&= \sum _{X \in {\text {Hom}}_{}(\mathbf {Z}_p^{r},G)/G} {\tilde{\upchi}} (|C_\Pi (X)|/C_G(X)) \end{aligned}$$

by Lemma A.3. $\square$

It is clear from Lemma A.4, but maybe not from Definition A.2, that all (p-primary) equivariant Euler characteristics are integers.

Appendix B. Eulerian Functions of Groups

Let G be a finite group acting on a finite poset $\Pi$. For any natural number $r \ge 1$, the rth reduced equivariant Euler characteristic (Defintion A.1) and the p-primary rth equivariant reduced Euler characteristic are

$$\begin{aligned}&{\tilde{\upchi}}_r(\Pi ,G) = \frac{1}{|G|}\sum _{X \in {\text {Hom}}_{}(\mathbf {Z}^r,G)} {\tilde{\upchi}} (C_{\Pi }(X)) = \frac{1}{|G|} \sum _{ B \le G} \varphi _{\mathbf {Z}^r}(B) {\tilde{\upchi}} (C_\Pi (B)) \end{aligned}$$

(B.1)

$$\begin{aligned}&{\tilde{\upchi}}_r(p,\Pi ,G) = \frac{1}{|G|} \sum _{X \in {\text {Hom}}_{}(Z_p^r,G)} {\tilde{\upchi}} (C_\Pi (X)) = \frac{1}{|G|}\sum _{ B \le G} \varphi _{Z_p^r}(B) {\tilde{\upchi}} (C_\Pi (B)) \end{aligned}$$

(B.2)

where $\varphi _{\mathbf {Z}^r}(B)$ ($\varphi _{Z_p^r}(B)$) is the number of epimorphisms of the abelian group $\mathbf {Z}^r$ ($Z_p^r =\mathbf {Z}\times \mathbf {Z}_p^{r-1}$) onto the subgroup B of G. In this appendix, we recall some of the properties, helpful for concrete computer assisted calculations of equivariant Euler characteristics, of the eulerian function $\varphi _{\mathbf {Z}^r}(B)$ [9].

For any finite group B, let ${\text {Hom}}_{}(\mathbf {Z}^r,B)$ and ${\text {Epi}}_{}(\mathbf {Z}^r,B)$ be the set of homomorphisms or epimorphisms of $\mathbf {Z}^r$ to B. Then ${\text {Hom}}_{}(\mathbf {Z}^r,B) =\coprod _{A \le B} {\text {Epi}}_{}(\mathbf {Z}^r,A)$ and $\varphi _{\mathbf {Z}^r}(B) = |\mathrm {Epi}(\mathbf {Z}^r,B)|$. (When $r=1$ and $C_n$ is cyclic of order n, $\varphi _{\mathbf {Z}^1}(C_n)$ is Euler’s totient function $\varphi (n)$.) We observe that $\varphi _{\mathbf {Z}^r}$ is multiplicative.

Lemma B.3

Let $B_1$ and $B_2$ be two finite groups of coprime order.

• (1) For any subgroup A of $B_1 \times B_2$, $A = A_1 \times A_2$ where $A_i$ is the image of A under the projection $B_1 \times B_2 \rightarrow B_i$, $i=1,2$.

• (2) $\varphi _{\mathbf {Z}^r}(B_1 \times B_2) = \varphi _{\mathbf {Z}^r}(B_1) \times \varphi _{\mathbf {Z}^r}(B_2)$ for any $r \ge 1$

Proof

Let $g_i$ be the order of $B_i$, $i=1,2$. The order of A, which divides $g_1g_2$, is of the form $k_1k_2$ where $k_1$ divides $g_1$ and $k_2$ divides $g_2$. The order of $A_i$ divides $k_1k_2$ and $g_i$. Thus $|A_i|$ divides $k_i$. It follows that the order of $A_1 \times A_2$ divides the order of A. But A is a subgroup of $A_1 \times A_2$ so $|A| = |A_1 \times A_2|$ and $A= A_1 \times A_2$. $\square$

Next, we compute $\varphi _{\mathbf {Z}^r}(C_p^d)$ where $C_p^d$ is elementary abelian of order $p^d$. First, ${\text {Epi}}_{}(\mathbf {Z}^r,C_p^d) = {\text {Epi}}_{}(C_p^r,C_p^d)$, the set of epimorphisms of $C_p^r$ onto $C_p^d$. Next, note that there is a bijection between the orbit set ${\text {Epi}}_{}(C_p^r,C_p^d)/{\text {Aut}}_{}(C_p^d)$ and the set of $(r-d)$-dimensional subspaces of $\mathbf {F}_p^r$ (kernels of epimorphisms). The number of such subspaces is the Gaussian binomial coefficient $\left( {\begin{array}{*{20}c}r\\ r-d\end{array}}\right) _p = \left( {\begin{array}{*{20}c}r\\ d\end{array}}\right) _p$ [24, Proposition 1.3.18]. Thus

$$\begin{aligned} \varphi _{\mathbf {Z}^r}(C_p^d) = |{\text {Epi}}_{}(\mathbf {Z}^r,C_p^d)| = \left( {\begin{array}{*{20}c}r\\ d\end{array}}\right) _p |{\text {GL}}^{+}_{d}(\mathbf {F}_{p})| = \prod _{j=0}^{d-1} (p^r-p^j) \end{aligned}$$

(B.3)

In the general case, the number of homomorphism of $\mathbf {Z}^r$ to B is

$$\begin{aligned} |{\text {Hom}}_{}(\mathbf {Z}^r,B)| = \sum _{A \le B}|{\text {Epi}}_{}(\mathbf {Z}^r,A)| = \sum _{A \le G}|{\text {Epi}}_{}(\mathbf {Z}^r,A)| \zeta (A,B) \end{aligned}$$

where $\zeta (A,B)=1$ if $A \le B$ and $\zeta (A,B)=0$ otherwise. The number of epimorphism of $\mathbf {Z}^r$ onto B is

$$\begin{aligned} \varphi _{\mathbf {Z}^r}(B) = |{\text {Epi}}_{}(\mathbf {Z}^r,B)| = \sum _{A \le G}|{\text {Hom}}_{}(\mathbf {Z}^r,A)| \mu (A,B) \end{aligned}$$

by Möbius inversion. Of course, $\varphi _{\mathbf {Z}^r}(B)>0$ if and only if B is abelian and generated by r of its elements. Assuming B is abelian, $|{\text {Hom}}_{}(\mathbf {Z}^r,A)|=|A|^r$ for any $A \le B$ so that [7, 9, 30]

$$\begin{aligned} \varphi _{\mathbf {Z}^r}(B) = |{\text {Epi}}_{}(\mathbf {Z}^r,B)| = \sum _{A \le B} |A|^r \mu (A,B) \end{aligned}$$

The Möbius function $\mu (A,B)=0$ unless $\Phi (B) \le A \le B$ and then $\mu _B(A,B) = \mu _{B/\Phi (B)}(A/\Phi (B),B/\Phi (B))$ where $\Phi (B)$ is the Frattini subgroup [7]. Therefore

$$\begin{aligned}&\varphi _{\mathbf {Z}^r}(B)= \sum _{A \le B} |A|^r \mu _B(A,B) = |\Phi (B)|^r \sum _{A \le B/\Phi (B)} |A|^r \mu _{B/\Phi (B)}(A,B/\Phi (B))\\&\quad =|\Phi (B)|^r \varphi _{\mathbf {Z}^r}(B/\Phi (B)) \end{aligned}$$

The abelian group B is the product, $B=\prod B_p$, of its Sylow $p$-subgroups, $B_p$. By multiplicativity (Lemma B.3.(2)),

$$\begin{aligned} \varphi _{\mathbf {Z}^r}(B) = \prod _p \varphi _{\mathbf {Z}^r}(B_p) \end{aligned}$$

The Frattini quotient $B_p/\Phi (B_p)$ is an elementary abelian p-group of order, say, $p^d$. We conclude that

$$\begin{aligned} \varphi _{\mathbf {Z}^r}(B_p) &= |\Phi (B_p)|^r |{\text {Epi}}_{}(\mathbf {Z}^r,C_p^d)| {\mathop {=}\limits ^{\text {(B.4)}}} |\Phi (B_p)|^r \prod _{j=0}^{d-1} (p^r-p^j) \\&= |B_p|^r \prod _{j=0}^{d-1} (1-p^{j-r}) \end{aligned}$$

For the final equality, use that if $B_p$ has order $p^m$, then the order of the Frattini subgroup is $p^{m-d}$ so that $|\Phi (B_p)|^r = p^{r(m-d)}$.

For a prime p, recall that $Z^r_p = \mathbf {Z}\times \mathbf {Z}_p^{r-1}$. In particular, $Z^1_p = \mathbf {Z}$ is independent of p. The number of epimorphisms of $Z_p^r$ onto B is

$$\begin{aligned} \varphi _{Z_p^r}(B) = \varphi _{Z_p^r} \left (\prod _s B_s \right) = \prod _s \varphi _{Z_p^r}(B_s) = \varphi _{\mathbf {Z}^r}(B_p) \prod _{s \ne p} \varphi _{\mathbf {Z}}(B_s) \end{aligned}$$

where $B_s$ is the Sylow $s$-subgroup of B. Here, $\varphi _{\mathbf {Z}}(B_s)=|B_s|(1-p^{-1})$ if $B_s$ is cyclic and $\varphi _{\mathbf {Z}}(B_s)=0$ otherwise. Thus $\varphi _{Z_q^r}(B)>0$ if and only if $B_q$ can be generated by r of its elements and $B_s$ is cyclic for all primes $s \ne q$.

Example B.5

The symplectic group $G={\text {Sp}}_{4}(\mathbf {F}_{2})$, of order 720, acts on the discrete poset $L={\text {L}}_4^*(\mathbf {F}_2)$ of 30 totally isotropic subspaces. Equation (B.1) with the data of Figure 2, found with the help of the computer algebra system Magma [3], shows that

$$\begin{aligned} -&{\tilde{\upchi}}_{r+1}(L, G) = -\frac{1}{720}(-16+80(3^{r+1}-1) - 36(5^{r+1}-1) - 10(3^{r+1}-1)(3^{r+1}-3))\\&\quad =\frac{1}{8}(3^r-1)^2 - \frac{1}{4}(3^r-5^r) \\ -&{\tilde{\upchi}}_{r+1}(3,L,G) = -\frac{1}{720}(-16+80(3^{r+1}-1) - 36 \cdot 4 - 10(3^{r+1}-1)(3^{r+1}-3))\\&\quad =\frac{1}{8}(3^r-1)^2 - \frac{1}{4}(3^r-1) \\ -&{\tilde{\upchi}}_{r+1}(5,L,G) = -\frac{1}{720}(-16+160 - 36 (5^{r+1}-1)) = \frac{1}{4}(5^r-1) \end{aligned}$$

in accordance with Example 6.8. By Lemma 4.2, in (B.1) we only need abelian subgroups of G of order prime to 2.

Fig. 2

Abelian $2'$-subgroups of ${\text {Sp}}_{4}(\mathbf {F}_{2})$